平底悬链线形明渠水力最优断面求解

韩延成，梁梦媛，Said M Easa，唐 伟，初萍萍，高学平



平底悬链线形明渠水力最优断面求解

韩延成1，梁梦媛1，Said M Easa2，唐 伟1，初萍萍1，高学平3

（1. 济南大学水利与环境学院，济南 250022；2. Department of Civil Engineering, Ryerson University, Toronto, M5B 2K3, Canada； 3. 天津大学水利工程仿真与安全国家重点实验室，天津 300072）

断面设计是渠道设计的重要内容之一，适宜的渠道断面不仅能够增加过流能力，提高输水效率，减小输水损失，还能降低建造成本。该文提出了一种具有平底和悬链线形侧边的明渠断面。这种断面将平底和悬链线侧边平滑连接，既具有平底断面建造容易、灵活，管护方便，底部容易压实，侧边和平底可以用不同材料建造（以降低成本）等优点，也具有悬链线形断面过流能力大、无应力集中拐角、不宜渗漏、防冻胀能力强，耐久性好等优点，可广泛应用于大、中、小型渠道及寒区，具有良好的实用价值。推导了过流面积、湿周、水面宽度等水力断面特性计算公式。提出了一个更简单的正常水深的迭代算法。基于拉格朗日乘子法，推导出了平底悬链线形明渠的水力最优断面，结果表明其水力最优断面的底宽与水深比、水面宽与水深比、底宽与形状系数比、水面宽度与形状系数比、形状系数与水深比均为常数：宽深比等于0.405，形状系数与水深比等于0.474，水面宽与水深的比值为2.112，底宽与形状系数的比值为0.855。与现有平底断面（梯形、平底抛物线形、平底半立方抛物线形）进行了比较，结果表明，在过流面积或湿周一定的情况下，平底悬链线形断面的过流能力最大，相反，在流量一定的情况下，平底悬链线形断面的过流面积、湿周、水面宽度是最小的。与传统的悬链线形渠道进行了比较，增加平底后，在同等条件下，平底悬链线形渠道水力最优断面的过流能力不仅没有降低，反而增加了，意味着其经济性也优于传统的悬链线断面。研究为平底悬链线形渠道设计提供理论支撑。

形状；水力学；渠道；平底；悬链线形；水力最优断面

0 引 言

中国有300多万千米长的渠道，每年有大量的渠道需要建设、改造。明渠断面设计理论对提高输水效率、减小输水损失、提高灌区农业发展、减小建造成本均有重要的意义[1-2]。过去，由于施工、衬砌、预制机具落后，渠道大多用简单梯形、矩形断面[1]，随着机械化衬砌、预制技术的发展，越来越多的输水工程采用曲线形或部分采用曲线形断面[3-5]，例如U形断面、抛物线形断面、弧形坡脚梯形断面。

根据渠道底部形状不同，传统的明渠断面可以分为2类：1）平底断面，包括梯形、矩形断面；2）曲线形断面，包括半圆形、抛物线形、悬链线形、蛋形等断面[1]。曲线形和平底断面均有各自的优缺点。学者们普遍认为曲线形断面有如下优点[4-11]：1）曲线形断面没有拐角，没有应力集中点，不易有应力集中导致的裂缝，因此渗漏少；2）曲线形断面从底部到顶部是逐渐扩大的，因而具有更好的边坡稳定性（特别是非衬砌渠道）；3）曲线形断面具有更大的过流能力和更好的水力学特性；4）曲线形断面的防冻胀、耐久性特性普遍优于梯形断面[12-15]，因而和使用寿命更长。正是曲线形断面的这些特点，使曲线形或复合曲线形断面成为灌区使用最广泛的渠道断面形式之一。例如U形断面底部采用了曲线形圆弧。虽然施工难度较梯形断面增大了，但其防渗漏、抗冻张、耐久性及过流能力均好于梯形断面，使其成为最广泛应用的断面之一。抛物线形断面是继梯形和U形断面之后发展的新断面，具有水流条件好，渠道不易淤积、抗冻胀能力强和节省耕地的特点, 并且随着施工机具的发展，抛物线形渠道在施工制模中更容易计算和控制，因此在水利水电工程、农田灌溉和排水及在南水北调工程中广泛应用[16-17]。河北省石津灌区、甘肃省洪水河灌区、宁夏引黄灌区都大量地使用了抛物线形断面混凝土衬砌防渗渠道，效果很好[16]。另外，广泛应用的圆形断面、马蹄形、城门洞、卵形均为纯曲线或部分曲线形断面，也是不可或缺的输水断面。学者们越来越重视新型渠道的研究，提出了许多创新断面。魏文礼等[18]提出了半立方抛物线形断面，Han等[9-10]提出了立方抛物线形断面和10/3次方抛物线形断面。学者们对新型渠道断面及曲线形断面的水力学特性展开了广泛的研究。Loganathan等[8,11]对抛物线形断面的设计及水力最优断面展开了深入研究，张宽地等[19]对圆形断面的水力特性进行了研究，梁元博等[20]对城门洞形、马蹄形断面进行了研究，文辉等[16,21-22]对抛物线形断面进行了研究。但曲线形断面也有缺点，例如建造的灵活性不如梯形断面，底部不易压实[3,6-7]，不宜应用于大型宽浅型渠道（受曲线函数的约束），另外由于曲线形断面只有2个曲线侧边，缺少平底部分会使维护增加难度[3,6]。平底断面（如梯形、矩形）具有底部施工工艺简单，底部容易压实，底宽可以变化，建造灵活等优点[4,7-8]，但其缺点是水力学特性不如曲线形断面，过流能力小且有明显的应力集中点和拐角，易造成裂缝和渗漏，易遭冻胀破坏[7,23]，耐久性不如无应力集中点的曲线形断面。

学者、工程师们在对曲线形断面大量研究的基础上，提出了各种新型复合断面，包括U形断面、弧形坡脚梯形、平底抛物线形断面等。Abdulrahman[24]提出了一种梯形底、矩形侧边的复合断面，Babaeyan-Koopaei[25]提出了一种抛物线形底三角形侧边的复合断面，Vatankhah[26]提出一种通用的多边形渠道。U断面是将圆形底和梯形侧边结合的复合断面，目前得到了广泛的工程实际应用。弧形坡脚梯形断面是一种平底圆角的复合断面[11,23]。相对于梯形断面，虽然其过流能力提高有限，但能使平底、圆角、侧边平滑连接，既有梯形断面的优点，又有曲线形断面的优点，其防冻胀特性优于梯形断面，衬砌板不易产生冻胀破坏[23]，具有良好的实用价值，是中国渠道防渗工程技术规范推荐使用的一种渠道形式[23]。另外，Das[7]提出了将平底和抛物线形侧边结合的平底抛物线渠道断面，Han[6]提出了平底的半立方抛物线形渠道及水力最优断面。Easa[27]（2009）[28]提出了两段式平底抛物线形断面，证明其较平底抛物线形断面具有更优的特性。Easa等[28-29]提出了平底的椭圆形渠道及最优断面。

悬链线形断面是水力学中重要的断面类型，具有优良的水力学特性，最优断面的过流能力较抛物线形断面过流能力还大[1,30]，本文结合梯形断面和悬链线形断面各自的优点，提出一种具有平底和悬链线形侧边的断面，理论上它既具有悬链线形断面无应力集中点，不易有应力集中导致的裂缝，渗漏少，稳定性好、水力特性优良、抗冻胀能力强等特征，也具有平底断面设计、建造灵活，施工难度小、管理和维护容易，底部容易压实等特性，具有良好的实用价值和应用前景。本文研究了其水力断面特性、正常水深及水力最优断面，以期为该断面工程应用提供理论支撑。

1 平底悬链线形渠道水力断面特性和正常水深

1.1 水力断面特性

传统的悬链线形断面是曲线形断面（图1a），形状可表示为[1]

式中为形状系数；为横坐标，m；为纵坐标，m；cosh为双曲余弦函数。

注：为悬链线形侧边部分对应水面宽度，m；为形状系数；为水深，m；为渠道底宽，m；为水面处的边坡系数；hc为平底悬链线形断面的水面总宽度，m。下同。

Note:is width of water surface for side portion of catenary section, m;is shape factor;is water depth, m;is bottom width, m;is side slope factor at water surface;hcis total width of water surface of horizontal-bottomed catenary section, m. Same as below.

图1 2种悬链线形断面

Fig. 1 Two types of catenary sections

平底悬链线形断面由1个平底和2条悬链线侧边组成，平底与侧边平滑连接，没有拐点，因而也没有应力集中点。如图1b所示，方程可表示为

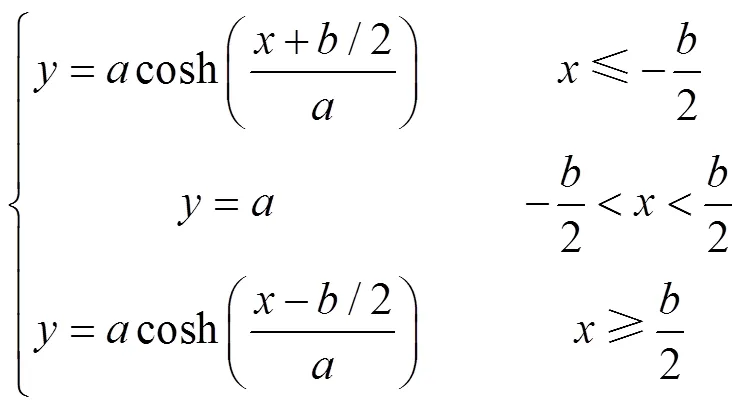
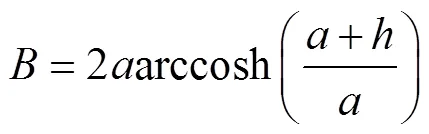
平底悬链线形断面面积可用积分法得到

式中hc为水深对应平底悬链线形断面面积，m2；sinh为双曲正弦函数。

湿周为平底和2个侧边长度之和，用积分法可得到

式中hc为湿周，m。

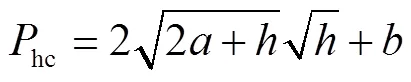
1.2 平底悬链线形渠道正常水深计算

1.2.1 正常水深计算公式

正常水深是明渠水力学的重要内容，在渠道设计、运行、水面线计算中广泛应用。正常水深与流量、糙率、底坡之间形成了复杂的非线性关系，大多数类型渠道断面没有显式直接求解公式[31]。学者们对正常水深的显式求解方法进行了大量的研究[17,19,32]，针对梯形、抛物线形、蛋形、马蹄形等各种断面提出了显式求解方法。迭代法是最常用的方法，其优点是计算简单，可以无限逼近理论解[31,33-35]。

正常水深的求解一般根据明渠均匀流计算中最常用的曼宁公式[1]表示如下

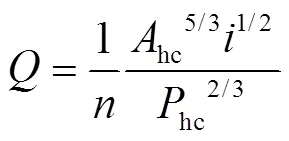
式中为流量，m3/s；为糙率；为渠底纵向比降。

将式（3）、式（6）和式（7）代入式（9），简化后可以得到流量和正常水深之间的关系为

可以看出，式（10）是一个高度非线性方程，不能显式求解正常水深，不方便工程应用，研究显式算法是必要的。

1.2.2 牛顿显式迭代显式算法

1）牛顿显式迭代显式算法推导

根据式（10）和式（11），可以得到牛顿迭代显式算法为

其中

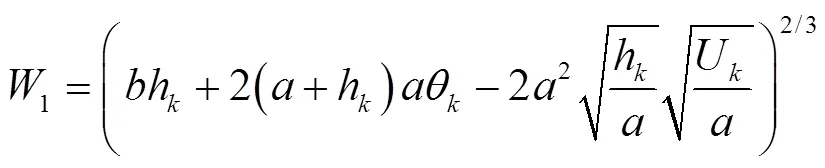
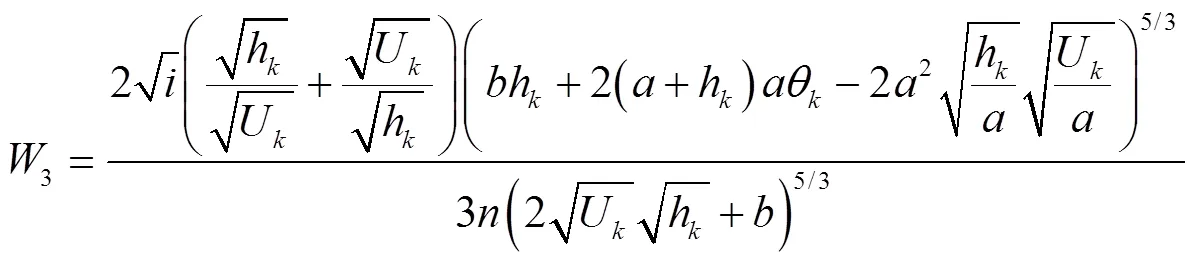
从式（12）可以看出，推导出的牛顿迭代算式虽然可以用来手工计算，但表达式还是比较复杂。

1.2.3 简单显式迭代算法

根据式（10），本文提出简单的显式迭代算法如下

根据迭代原理[38]，式（16）收敛的条件是

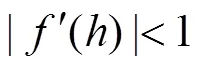
式中

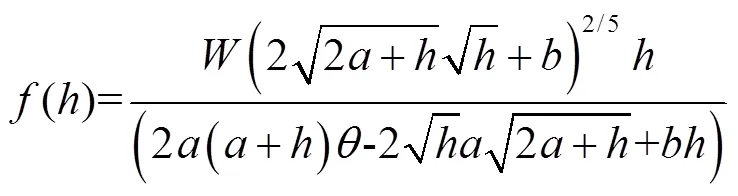
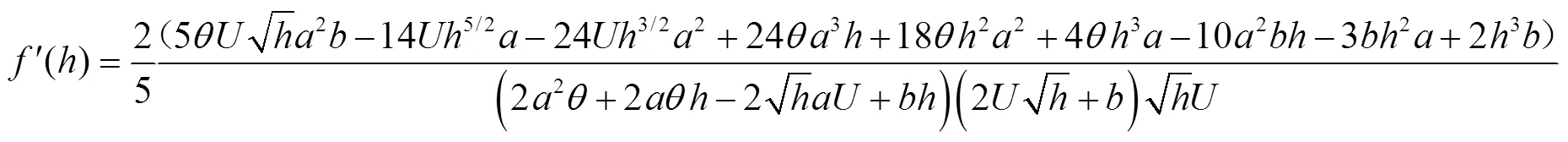
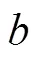
1.3 平底悬链线形断面的水力最优断面推导

1.3.1 底悬链线形断面的水力最优断面模型

根据水力学，水力最优断面为流量一定的情况下，过流断面的面积最小的断面[1,3,4,6]，可表示为

目标函数

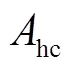
约束条件

1.3.2 水力最优断面的推导

根据最优化方法中的拉格朗日乘子法，式（22）和（23）可表示为（Rao，2009）

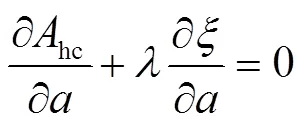
式中为拉格朗日乘子，为约束函数。由式（24）和式 （25），消掉可得到

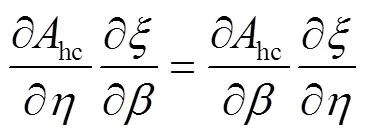
同样，由式（24）和式（26），消掉得到

根据式（23），对求关于、和的导数，并代入式（27）和式（28）得到：

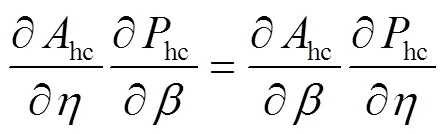
以上2式是求解平底悬链线形渠道水力最优断面的微分方程。下面根据式（29）和式（30）求解平底悬链线形渠道水力最优断面的具体参数。

同样，根据式（21），求hc关于、和的导数分别为

将式（31）代入式（29），式（32）代入式（30），简化后得到

联接方程组（33），可以得到= ±3.602，= ±0.855。由于工程中、、均为大于0的值，因此平底悬链线形渠道水力最优断面2个最重要的参数为

根据式（34）和式（35）可以得到水面宽与形状系数比为

根据式（3）和式（34），可以得到水力最优断面形状系数和水深之间的关系为

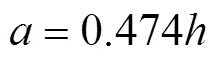
由式（35）和式（37）可以得到水力最优断面的宽深比为

根据式（34）～式（37），可以得到与的比率和B与的比率分别为

1.3.3 水力最优断面的水力学计算公式

1）已知水深求流量

将式（34）～（38）代入式（6）、式（7），可以得到计算hc和hc的直接求解公式

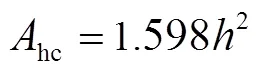
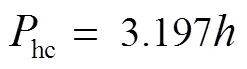
将hc和hc代入式（9），可以得到流量的直接计算公式为

2）已知流量求水深

利用式（44）～（37），可以得到已知流量求、hc、hc和hc的表达式为

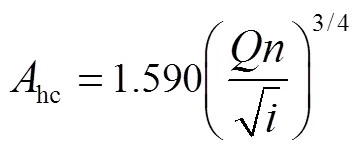
3）正常水深和临界水深

显然水力最优断面条件下正常水深就是式（44），是一个显式公式。临界水深是水力学的另一个重要参数，在水面线，水跃等水力学计算中广泛应用。临界水深的通用计算公式为

式中为动能修正系数；为重力加速度，m/s2。将式（40）和（41）代入式（49），解方程可以得到临界水深h的显式求解公式为

2 应用案例及结果分析

2.1 平底悬链线形渠道水力最优断面公式应用案例

1）某地要建设一条渠道，已知糙率=0.014，渠底纵坡=1/20 000，流量=25.0 m3/s。要求按水力最优断面设计平底悬链线形渠道并求水面宽度、过水断面面积和湿周。

注：为悬链线形侧边部分对应水面宽度与形状系数之比；为底宽与形状系数之比。

Note:is ratio of water surface width of side portion for catenary section () to shape factor ();is ratio of bottom width () to shape factor ().

图2 过水断面面积hc和、之间的关系

Fig. 2 Relationship between flow areahcandand

2.2 与平底及梯形明渠断面比较

梯形断面、矩形断面是应用最广泛的断面类型。另外，由于其兼有平底和抛物线形断面的优点，平底抛物线形断面水力最优断面的过流能力较同样条件下的梯形断面大，得到大量的学者认可和关注[3,7,28]。本文提出的平底悬链线形断面过流能力是否能达到平底抛物线形断面或接近呢？

2.2.1 与平底及梯形断面水力特性比较

1）与平底抛物线形断面比较

平底抛物线形断面由平底和抛物线形侧边组成 （2007）[3,7]，其形状定义为[3]

与平底抛物线形断面对比（表1）可以看出，在过水断面面积或湿周相同的条件下，平底悬链线形断面的过流能力大于平底抛物线形断面。在流量相同的条件下，平地悬链线形断面的过流断面面积、湿周、水面宽度均小于平底抛物线形断面，意味着其土方成本、衬砌成本、征地费均减小平底抛物线形断面。

平底半立方抛物线形断面是一种具有平底和半立方抛物线侧边的组合断面，Han[6]研究了其水力最优断面及其特性（结果如表1所示）。对比结果表明，在过水断面面积或湿周相同的条件下，本文提出的平地悬链线形断面的过流能力大于平底半立方抛物线形断面。在流量相同的条件下，平地悬链线形断面的过流断面面积、湿周、水面宽度均小于平底半立方抛物线形断面，是一种更经济的断面。

表1 悬链线形渠道与现有渠道水力最优断面水力特性比较

在机械化衬砌和预制渠道越来越广泛应用的背景下，建造的土渠越来越少，曲线形渠道与梯形渠道的建造难度差别越来越小。湿周的减小可以减小衬砌费用，水面宽度的减小可以减小征地费，过水断面的减小可以减小土方费用。更重要的是，本文提出的断面，平底和侧边平滑连接，无应力集中点，可以减小由于应力集中造成的裂缝[6-8]，是一种非常实用的断面。

2.2.2 案例分析

2）按其他平底断面设计：用同样的方法，利用表1中的公式，可以得到按梯形断面、平底半立方抛物线形断面、平底抛物线形断面设计的水力最优断面结果如表2所示。对比结果表明，平底悬链线形断面的过流面积、湿周和水面宽度均是最小的。

表2 不同断面类型得到的水力最优断面结果

2.3 与传统悬链线形断面比较

传统悬链线形断面具有良好的水力学特性[1,30]。虽然本文作者认为平底悬链线形断面相对于传统悬链线形断面，其最大的优点是灵活性。但增加平底后，需要研究水力最优断面水力学特性是否降低。

由图1可以看出，传统的悬链线形断面是平底悬链线形断面的一种特殊形式。设=0，则式（2）为传统的悬链线形断面。同时将=0代入平底悬链线形断面的断面面积与湿周计算式（6）和式（7），可以得到传统悬链线形断面的面积和湿周计算公式为

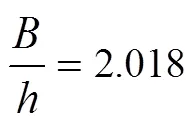
与求解平底悬链线形最优断面的方法相似（式（41）～式（48）），可以得到悬链线形最优断面的过水断面面积、湿周、水面宽度的显式计算公式（如表2所示）。对比结果显示，增加平底后水力最优断面水力特性并没有降低。在过水断面面积或湿周相同的条件下，平底悬链线形断面的过流能力大于传统悬链线形断面；在流量相同的条件下，平底悬链线形断面的过流断面面积、湿周、水面宽度均小于传统悬链线形断面。意味着土方成本、衬砌成本、征地费均减小了。从图1、图2对比可以看出，加平底后，建造更加灵活了（渠道宽度可以随底宽灵活调节）。另外，平底悬链线形断面加平底后，由于施工机械可以进入渠道施工，显然施工难度降低了，测量人员可以站在底部放线，平底的精度更容易控制，底部也容易压实，可以避免一般曲线形断面底部容易空洞的问题[3,6]，管护时，人可以站在底部操作，机械可以在底部行走，管护也方便了[3,6]。更重要的是，正如著名的渠道设计专家Das指出的那样，曲线形侧边加侧边后，就可以像梯形断面一样，侧边和底部采用不同的材料，以减小建造成本，或增加防渗效果[7]。因此平底悬链线形是一种非常实用的断面。

3 结 论

2）平底悬链线形断面与平底断面相比，与现有的平底断面（梯形、平底抛物线形、平底半立方抛物线形断面）比较，在同等条件下（过流面积或湿周相同），平底悬链线形最优断面的过流能力最大。相反，在过流量一定的情况下，平底悬链线形最优断面具有最小的过流面积和湿周，这意味着，平底悬链线形断面的在流量一定的情况下，需要更少的土方量，更小的衬砌量和更少的征地费，因而更经济。同时其具有平底断面建造灵活（底部容易压实、宽度可以随底宽灵活调整，底部和侧边可以采用不同材料以减小成本或增加防渗效果等）、施工难度降低、管护方便等优点。

3）与传统的悬链线形断面相比，与传统的悬链线形渠道比较结果表明，增加平底后，在同等条件下，平底悬链线形渠道水力最优断面的过流能力增加了。相反，在过流量一定的情况下，平底悬链线形最优断面具有更小的过流面积和湿周、水面宽度，意味着，衬砌量、土方量和征地费更小，经济性、实用性更高。同时其还具有传统的悬链线形断面无应力集中拐点、过流能力大、渗漏量小、不宜破坏、抗冻胀能力强的特点，因而其实用性更强，应用前景广阔。

[1] Chow V T. Open Channel Hydraulics[M]. New York: McGraw-Hill, 1959.

[2] Jain A, Bhattacharjya R K, Sanaga S. Optimal design of composite channels using genetic algorithm[J]. Journal of Irrigation & Drainage Engineering, 2004, 130(4): 286－295.

[3] Han Yancheng, Gao Xueping, Xu Zhenghe. The best hydraulic section of horizontal-bottomed parabolic channel section[J]. 水动力学研究与进展B辑，2017，29(2): 305－313.

[4] 韩延成，徐征和，高学平，等. 二分之五次方抛物线形明渠设计及提高水力特性效果[J]. 农业工程学报，2017，33(4)：131－136. Han Yancheng, Xu Zhenghe, Gao Xueping, et al. Design of two and a half parabola-shaped canal and its effect in improving hydraulic property[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(4): 131－136. (in Chinese with English abstract)

[5] 罗金耀，王长德，夏富洲，等. 大型输水渠道系统优化设计研究[J]. 水利学报，1996(6)：24－28. Luo Jinyao, Wang Changde, Xia Fuzhou, et al. Optimization design of large-scale water conveyance channel system[J]. Journal of Hydraulic Engineering, 1996(6): 24－28. (in Chinese with English abstract)

[6] Han Yancheng. Horizontal bottomed semi-cubic parabolic channel and best hydraulic section[J]. Flow Measurement & Instrumentation, 2015, 45: 56－61.

[7] Das A. Optimal design of channel having horizontal bottom and parabolic sides[J]. Journal of Irrigation & Drainage Engineering, 2007, 133(2): 192－197.

[8] Loganathan G V. Optimal design of parabolic canals[J]. Journal of Irrigation & Drainage Engineering, 1991, 117(5): 716－735.

[9] Han Yancheng, Easa S M. New and improved three and one-third parabolic channel and most efficient hydraulic section[J]. Canadian Journal of Civil Engineering, 2017, 44(5): 387–391.

[10] Han Yancheng, Easa S M. Superior cubic channel section and analytical solution of best hydraulic properties[J]. Flow Measurement & Instrumentation, 2016, 50: 169－177.

[11] Mironenko A P, Willardson L S, Jenab S A. Parabolic canal design and analysis[J]. Journal of Irrigation & Drainage Engineering, 1984, 110(2): 241－246.

[12] 郑文锦，林琳. U形断面抗冻胀能力优越性分析[J]. 水利与建筑工程学报，2006，4(1)：51－53. Zheng Wenjin, Lin Lin. Advantages of U-shaped section for frost heaving resistance [J]. Journal of Water Resources and Architectural Engineering, 2006, 4(1): 51－53. (in Chinese with English abstract)

[13] 杨汉林. 实用弧形坡脚梯形断面的设计[J]. 中国农村水利水电，2000(12)：28－31. Yang Hanlin. Design of practical curved slope trapezoidal section[J]. China Rural Water and Hydropower, 2000(12): 28－31. (in Chinese with English abstract)

[14] 王正中，李甲林，陈涛，等. 弧底梯形渠道砼衬砌冻胀破坏的力学模型研究[J]. 农业工程学报，2008，24(1)：18－23. Wang Zhengzhong, Li Jialin, Chen Tao, et al. Mechanics models of frost-heaving damage of concrete lining trapezoidal canal with arc-bottom[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2008, 24(1): 18－23. (in Chinese with English abstract)

[15] 宋清林. 抛物线形混凝土衬砌渠道冻胀破坏力学模型及数值模拟[D]. 杨凌：西北农林科技大学，2015. Song Qinglin. Mechanical Model and Numerical Simulation of Frost Heaving Failure of Parabolic Concrete Lining Channel [D]. Yangling: Northwest A&F University, 2015. (in Chinese with English abstract)

[16] 文辉，李风玲. 数值积分法计算抛物线形渠道恒定渐变流水面线[J]. 农业工程学报，2014，30(24)：82－86. Wen Hui, Li Fengling. Numerical integration method for calculating water surface profile of gradually varied steady flow in parabola shaped channel[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(24): 82－86. (in Chinese with English abstract)

[17] 张新燕，吕宏兴. 抛物线形断面渠道正常水深的显式计算[J]. 农业工程学报，2012，28(21)：121－125. Zhang Xinyan, Lü Hongxing. Explicit solution for normal depth in parabolic-shape channel[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012, 28(21): 121－125. (in Chinese with English abstract)

[18] 魏文礼，杨国丽. 立方抛物线形渠道水力最优断面的计算[J]. 武汉大学学报，2006，39(3)：49－51. Wei Wenli, Yang Guoli. Calculation of optimal hydraulic cross-section for cubic parabola-shape channel [J]. Journal of Wuhan University, 2006, 39(3): 49－51. (in Chinese with English abstract)

[19] 张宽地，吕宏兴，赵延风. 明流条件下圆形隧洞正常水深与临界水深的直接计算[J]. 农业工程学报，2009，25(3)：1－5. Zhang Kuandi, Lü Hongxing, Zhao Yanfeng. Direct calculation for normal depth and critical depth of circular section tunnel under free flow [J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2009, 25(3): 1－5. (in Chinese with English abstract)

[20] 梁元博，马吉明，谢省宗. 城门洞形及马蹄形输入隧洞内的水跃[J]. 水利学报，2000，31(7)：20－24. Liang Yuanbo, Ma Jiming, Xie Shengzong. Hydraulic jumps in rectangular conduit with circular upper wall and horseshoe tunnel[J]. Journal of Hydraulic Engineering, 2000, 31(7): 20－24. (in Chinese with English abstract)

[21] 赵延风，宋松柏，孟秦倩. 抛物线形断面渠道收缩水深的直接计算方法[J]. 水利水电技术，2008，39(3)：36－37. Zhao Yanfeng, Song Songbai, Meng Qinqian. A direct calculation method for water depth in parabolic-shaped channel with contracted section[J]. Water Resources and Hydropower Engineering, 2008, 39(3): 36－37. (in Chinese with English abstract)

[22] 张志昌，贾斌，李若冰，等. 抛物线形渠道的水力特性[J]. 水利水运工程学报，2015(1)：61－67. Zhang Zhichang, Jia Bin, Li Ruobing, et al. Hydraulic characteristics of parabolic channels[J]. Journal of Water Resources and Hydropower Engineering, 2015(1): 61－67. (in Chinese with English abstract)

[23] 汪艺义. 弧形坡脚梯形渠道中弧形半径的确定[J]. 水利规划与设计，2017(1)：115－117. Wang Yiyi. Determination of radius radius in trapezoidal channel of curved slope[J]. Water Resources Planning and Design, 2017(1): 115－117. (in Chinese with English abstract)

[24] Abdulrahman A. Best hydraulic section of a composite channel[J]. Journal of Hydraulic Engineering, 2007, 133(6): 695－697.

[25] Babaeyan-Koopaei K, Valentine E M, Swailes D C J. Optimal design of parabolic-bottomed triangle canals[J]. Journal of Irrigation and Drainage Engineering, 2000, 126(6): 408－411.

[26] Vatankhah A R. Semi-regular polygon as the best hydraulic section in practice (Generalized solutions)[J]. Flow Measurement & Instrumentation, 2014, 38(8): 67－71.

[27] Easa S M. Improved channel cross section with two-segment parabolic sides and horizontal bottom[J]. Journal of Irrigation & Drainage Engineering, 2009, 135(3): 357－365.

[28] Easa S M. Versatile general elliptic open channel cross section[J]. Ksce Journal of Civil Engineering, 2016, 20(4): 1572－1581.

[29] Easa S M, Vatankhah A R. New open channel with elliptic sides and horizontal bottom[J]. Ksce Journal of Civil Engineering, 2014, 18(4): 1197－1204.

[30] 吕宏兴，冯家涛. 明渠水力最佳断面的比较[J]. 人民长江，1994(11)：42－45. Lü Hongxing, Feng Jiatao. Comparison of the best hydraulic sections in open channels[J]. People’s Yangtze River, 1994(11): 42－45. (in Chinese with English abstract)

[31] 韩延成，初萍萍，梁梦媛，等. 冰盖下梯形及抛物线形输水明渠正常水深显式迭代算法[J]. 农业工程学报，2018，34(14)：101－106 Han Yancheng, Chu Pingping, Liang Mengyuan, et al. Explicit iterative algorithm of normal water depth for trapezoid and parabolic open channels under ice cover[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(14): 101 －106. (in Chinese with English abstract)

[32] 张新燕，吕宏兴，朱德兰. U形渠道正常水深的直接水力计算公式[J]. 农业工程学报，2013，29(14)：115－119. Zhang Xinyan, Lü Hongxing, Zhu Delan. Direct calculation formula for normal depth of U-shaped channel[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013, 29(14): 115－119. (in Chinese with English abstract)

[33] Bijankhan M, Kouchakzadeh S. Egg-shaped cross section: Uniform flow direct solution and stability identification[J]. Flow Measurement & Instrumentation, 2011, 22(6): 511－516.

[34] Li Yonghong, Gao Zhaoliang Explicit solution for normal depth of parabolic section of open channels[J]. Flow Measurement & Instrumentation, 2014, 38(2): 36－39.

[35] Zhang X Y, Wu L. Direct solutions for normal depths in curved irrigation canals[J]. Flow Measurement & Instrumentation, 2014, 36(4): 9－13.

Optimal hydraulic section of horizontal-bottom catenary channel

Han Yancheng1, Liang Mengyuan1, Said M Easa2, Tang Wei1, Chu Pingping1, Gao Xueping3

(1.250022,; 2.M5B 2K3,300072)

A suitable channel section cannot only increase flow capacity of channel, improve efficiency of water resources, and reduce water leakage loss, but also decrease construction cost. This paper proposed a channel section with a horizontal bottom and catenary sides (HBC). The HBC section, on one hand, provided a larger flow capacity, lesser-sharp angles of stress concentration, less leakage, better slope stability and frost heave resistance than trapezoids and rectangles sections. On the other hand, it had lots of advantages of horizontal bottom sections, such as simpler construction, easier leveling and compaction of the foundation, and lesser construction cost. The most important advantage of this section was that the horizontal bottom and sides could be built with different materials or thickness for decreasing the construction cost or other purposes. The shape function for HBC was defined. The formulas for the flow area, wetted perimeter, and water surface width were presented. A simpler iterative algorithm for calculation of the normal depth was developed. The iterative convergence by this algorithm was evidenced. Comparisons showed that this simpler iterative algorithm was better than classic Newton iterative algorithm. The optimal model of the best hydraulic section of HBC was built. The general differential equations for all the sections having horizontal bottomed and curve sides were derived. The best hydraulic section of HBC channel was obtained according to Lagrange multiplier method and its characteristics were presented including shape factor, ratio of horizontal bottom width to shape factor etc. The results showed that the following optimum parameters were constant for the best hydraulic HBC section: bottom width to water depth, water surface width to depth, bottom width to shape factor, water surface width to shape factor, shape factor to water depth equals. The ratio of water surface width for catenary part to shape factor equaled 3.602, the ratio of bottom width to shape factor equaled 0.855, the ratio of bottom width to water depth equaled 0.405, and the ratio of shape factor to water depth equaled 0.474, and the ratio of total water surface width to water depth equaled 2.112. Various explicit formulae to calculate the normal depth, critical depth, shape factor, flow area, wetted perimeter and water surface width of the HBC section were derived for the best hydraulic section for HBC channel. These formulas should make the design of the HBC section easier and promote its practical applications. The optimum parameters of the best hydraulic section for existing horizontal bottom (HB) sections, such as trapezoidal, rectangle, horizontal bottomed parabolic, and horizontal bottomed semi-cubic parabolic were derived. The comparison results showed that the HBC section had larger discharge than those of existing horizontal bottom (HB) sections under the same conditions. In addition, the flow area, wetted perimeter, and water surface of the HBC section were the smallest, which means that earthwork cost, lining cost and land expropriation cost are all decreased, which means HBC section is more economical. Comparison with classic catenary section showed that the discharge of the HBC was larger than that of the classic catenary section under the same conditions. The flow area, wetted perimeter and water surface of the HBC were smaller than these of the classic catenary section, which means the HBC section has better hydraulic characteristics. Its economy was also superior to the traditional catenary section. The results were verified by examples. The proposed section should enrich existing types of open channel sections. The research provides a new practical and flexible channel section for channel design and theoretical support for horizontal-bottom catenary channel design and applications.

shapes; hydraulics; channels; horizontal bottom; catenary; best hydraulic section

2018-07-31

2019-02-10

山东省自然科学基金（ZR2017LEE028）；山东省“一事一议”（周飞艨）人才计划项目；山东省重点研发计划（2016GSF117038）；国家“十二五”科技支撑计划（2015BAB07B02-6）

韩延成，教授，博士，主要从事水力学及河流动力学方面研究。Email：stu_hanyc@ujn.edu.cn

10.11975/j.issn.1002-6819.2019.06.011

TV 131.4

A

1002-6819(2019)-06-0090-10

韩延成，梁梦媛，Said M Easa，唐 伟，初萍萍，高学平. 平底悬链线形明渠水力最优断面求解[J]. 农业工程学报，2019，35(6)：90－99. doi：10.11975/j.issn.1002-6819.2019.06.011 http://www.tcsae.org

Han Yancheng, Liang Mengyuan, Said M Easa, Tang Wei, Chu Pingping, Optimal hydraulic section of horizontal-bottom catenary channel[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(6): 90－99. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2019.06.011 http://www.tcsae.org