长时间序列气象数据结合随机森林法早期预测冬小麦产量

刘峻明，和晓彤，王鹏新，黄健熙



长时间序列气象数据结合随机森林法早期预测冬小麦产量

刘峻明1,3，和晓彤1,3，王鹏新2,3，黄健熙1

（1. 中国农业大学土地科学与技术学院，北京 100083；2. 中国农业大学信息与电气工程学院，北京 100083；3. 农业部农业灾害遥感重点实验室，北京 100083）

冬小麦生育早期的产量预测对于制定冬小麦整个生长期的精准管理决策具有重要参考意义。该文基于随机森林算法，采用1990—2015年河南省小麦平均拔节期至平均抽穗期地面观测气象数据与统计产量数据，分别提取不同穗分化期的温湿度、降水等47个气象要素和小麦种植区经纬度、高程3个空间要素，共计50个参数作为特征变量集，以实际单产、气象产量和相对气象产量分别作为目标变量，构建多种变量组合模型对冬小麦产量进行回归预测，并结合袋外数据重要性结果对产量影响因子进行分析。研究结果表明：1）使用气象产量和相对气象产量作为目标变量建模的预测效果优于单产模型，决定系数2均达到0.8以上，气象产量的平均绝对误差（mean absolute error，MAE）和均方根误差（root mean square error，RMSE）分别为415和558 kg/hm2，相对气象产量的MAE和RMSE分别为0.07和0.09；2）相较于气象特征，空间特征在产量预测中起决定性作用，且小花分化期以及抽穗开花期的气象特征产量预测精度高于其他穗分化期；3）在气象特征中，利用袋外数据变量重要性得出平均温度、最低温度、负积温、最高温度在不同生育阶段对产量的影响程度。该研究结果为冬小麦生育早期产量预测提供了新的思路和方法。

模型；温度；随机森林；产量预测；冬小麦

0 引 言

冬小麦的产量受生产技术水平、气象条件等多重影响，其生长环境是非常复杂的非线性系统，产量可看成是一段时期内温度、降水量、生长发育状况等多个影响因子相互叠加的结果。目前关于农作物产量预测的研究方法多以作物生长机理模型或经验模型为主[1]。作物生长机理模型通过输入研究区作物、气象、土壤和栽培措施等参数，对作物生长及产量形成过程进行动态模拟，适用于点尺度的模拟和预测，基于数据同化方法可以将作物生长机理模型与遥感数据进行同化，实现面尺度的作物产量预测，但由于参数众多，误差累积往往导致精度不够高[2-4]；经验模型通过构建作物影响因子与单产之间的统计关系进行估产，如利用卫星数据反演的气象参数[5]、遥感植被指数[6]等，建立与其农作物产量之间的线性回归模型，但通常存在经验特征强、容易过拟合的缺点。随着计算机技术的发展，近些年来机器学习方法也被应用到作物产量预测研究中，取得较好的效果。黎锐等[7]利用多时相遥感数据和支持向量机（support vector machine，SVM）对冬小麦进行估产，该方法核函数的选取以及参数的确定具有经验性，对精度有所影响[8]；姜新等[9-10]分别建立了基于叶面积指数、生物量等作物参数以及农机水平的人工神经网络（artificial neural network，ANN）产量预测模型，但其训练过程存在收敛速度慢和易陷入局部极值的问题，且模型参数较为复杂[11-12]。随机森林（random forest，RF）是一种基于分类与回归树的机器学习算法，由Breiman于2001年提出[13]，相较于传统决策树构建方法，其优越性体现在同等运算率下的高预测精度，以及在处理多维特征上对多重共线性并不敏感的特性[14]，目前在农作物产量预测方面，也取得了优于SVM、BP神经网络等算法的性能，且模型构建过程相对简单[15-16]；Everingham等[17]基于高光谱数据，认为RF能较好地进行作物产量预测；Tulbure等[18]利用RF识别了影响柳枝稷产量的包括降水、土壤肥料等多种关键因子。上述研究虽达到较好预测效果，但在特征选择方面欠缺深入研究以及较少考虑多时期气象特征对作物的影响。

因此本文基于随机森林算法，以河南省为研究区域，结合地面观测气象数据与冬小麦实际单产数据，选择不同特征及目标变量构建冬小麦产量预测模型，并对模型预测结果及气象特征影响进行分析，以期为区域冬小麦产量预测提供服务。

1 材料与方法

1.1 研究区域

河南省位于31°23′～36°22′N，110°22′～116°38′E，属北亚热带湿润气象与暖温带半湿润季风气象的过渡气象，年均降水量为500～1 000 mm，降水季节分布不均，全年50%的降水集中在夏季。河南省冬小麦多种植冬性、弱冬性品种，一般在9月中下旬至10月上旬播种，12月中旬后进入越冬期，翌年2月下旬开始进入返青期，3月中下旬进入拔节期，4月中下旬进入抽穗期，5月底至6月初成熟。

1.2 数据来源

河南省冬小麦单产资料来自《河南省统计年鉴》[19]中以县级行政区为单元的冬小麦单产数据，在1990—2015年间连续种植冬小麦的县市共106个，空间位置信息来自县市内气象观测站，分布情况如图1，剔除各县市单产缺失年份，共获得2 740个有效单产数据，将这些数据作为本研究的单产样本数据。气象资料来自中国气象科学数据共享服务网的《中国地面气象资料数据集（V3.0）》，提取1990—2015共26 a的逐日气象观测资料，对于没有气象资料的县市，采用地理信息系统的插值方法生成相应的气象数据。

图1 河南省冬小麦种植区分布Fig.1 Distribution of winter wheat planting area in Henan Province

1.3 研究方法

1.3.1 随机森林回归模型的构建

1）特征集及目标变量构造

由于拔节至抽穗期间是冬小麦发育最为敏感的阶段，是影响产量最重要的时期[20]。将该时段内气象、物候、地理位置作为产量影响因子。随机森林特征变量集如下：

首先，考虑总研究时段内的气象要素，提取河南省每年平均拔节至平均抽穗期内（3月14日—5月8日）的最高气温（max）、最低气温（min）、累计降水量（P）、负积温（AT）、有效积温（AT），总计5个特征。

其次，为体现不同时间阶段气象条件的影响，根据小麦穗分化进程[21]，将拔节至抽穗期按8 d为单位进行分段，得到7个时间段，与穗分化期大致对应关系为：小花分化前期（3月14日—3月21日）、小花分化后期（3月22日—3月29日)、雌雄蕊分化期（3月30日—4月6日)、药隔前期（4月7日—4月14日)、药隔后期（4月15日—4月22日)、四分体时期（4月23日—4月30日)、抽穗开花期（5月1日—5月8日)。生成各穗分化期内的max、平均气温（avg）、min、最大气温日较差（T）、平均相对湿度（hu）、P，总计42个特征。

最后，采用冬小麦种植区县市内气象观测站的经纬度（onat）和高程数据（le）共计3个变量作为空间特征。

农作物的产量可以划分为趋势产量、气象产量和误差部分。趋势产量用于表达因技术革新或社会进步因素而形成的产量，气象产量用于表示气象因子变化所带来的短期波动的产量，其他因素导致的表示为误差部分[22]。计算公式如下：

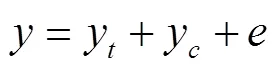
式中为实际产量，kg/hm2，y为趋势产量，kg/hm2，y为气象产量，kg/hm2，为误差部分。

趋势产量对气象产量存在一种平滑的作用，可以看作是以时间为自变量而进行的线性或非线性模拟。本文假设农业技术的提高对作物产量的影响呈平稳变化，忽略误差因素，对单产时间序列采用5a滑动平均法计算得到趋势产量，对于起始年份趋势值，依次倒推往年相对应的产量数据，河南省各年单产均值和趋势产量曲线如图2。为消除年代间的农业生产水平差异，利用各年各县市实际单产减去趋势产量得到气象产量，同时利用气象产量除以趋势产量获得相对气象产量以反映年际间气象差异造成的产量波动。分别使用单产、气象产量以及相对气象产量作为随机森林模型的目标变量，构建3种产量预测模型。公式如下：

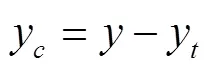
式中y为相对气象产量。

图2 河南省1990—2015年冬小麦趋势产量

2）特征变量相关性分析

图3为1990—2015年间不同穗分化期气象要素以及空间特征的关联热图，黄色表示强相关，蓝色表示弱相关。图3a为拔节至抽穗期总时段内空间特征（onatle），气象特征（maxminPATAT）之间的相关性，可以看出，on和le之间相关性较强，这是由河南省西高东低的地势造成的；由于气象因子年际差异较大，经纬度、高程与各气象要素之间的相关性均较弱；图3b～图3h分别为小花分化前期、小花分化后期、雌雄蕊分化期、药隔前期、药隔后期、四分体时期和抽穗开花期各气象要素之间的相关性，可以看出，从拔节期开始max和avg以及avg和min之间在各时段内存在较强相关性，但max和min的相关性较弱；T、hu和P在各时段内的相关性均较弱；相比其他时期，药隔后期的气象特征之间相关性较高。因此，最终选取onat、le作为空间特征变量，不同时期的maxavgminT、PATAT作为气象特征变量。

注：Lon、Lat、Ele、Tmax、Tavg、Tmin、Td、Ps、Rhu、NAT、AAT、yw分别表示经度、纬度、高程、最高气温、平均气温、最低气温、最大气温日较差、累计降水量、平均相对湿度、负积温、有效积温、相对气象产量。

3）构建过程

随机森林是由多棵分类回归树（classification and regression tree，CART）构成的组合分类模型[13]，各年份各县市的特征数据和产量数据进行集成共同构成随机森林的样本数据集，通过自助法（bootstrap）从原始样本集采样得到构建棵树所需的个子集，每次未被抽到的数据称为袋外数据（out-of-bag，OOB），用来进行内部误差估计和变量重要性评价；生成每棵树时，从规模为的特征变量集中随机选择个变量（），对于回归，采用均方差作为节点分裂标准，递归执行选取最优分枝的操作。由于随机森林采用样本和特征的双重随机抽样构建决策树，因此即使不对决策树进行剪枝操作也不会出现传统CART决策树过拟合的现象[14]。最后将这些树的结果取平均值即为目标变量的预测值。在RF算法中，根据试验结果实时优化决策树数目和创建分枝所需特征变量个数这2个参数。

1.3.2 变量重要性分析

随机森林可以解释若干自变量对因变量的作用。通过模型内部重要性结果，分析不同特征变量对产量的影响程度。其基本思想是：对于变量V，首先计算每棵树相应的袋外数据OOB的误差率EROOB；然后，对袋外数据中的变量V值进行随机的序列改变，而其他所有变量在保持不变的情况下，重新计算改变顺序后的袋外数据OOB的误差率EROOB，通过分析袋外数据序列改变时误差的增加情况来估计某一特征变量的重要程度[13]。变量V引起袋外误差增加的越大，精度减少的越多，说明该变量越重要。变量V的重要性表示为

式中为随机森林算法中树的数量，为个特征中变量的位置。

1.4 模型精度评价与验证

采用以下3个指标作为评价模型拟合程度优劣，即决定系数（coefficient of determination，2）、均方根误差（root mean square error，RMSE）和平均绝对误差（mean absolute error，MAE）[23-24]。

2 结果与分析

2.1 不同目标变量验证结果对比

以1990—2009年2 107组数据作为训练样本，使用全部特征变量，分别以单产、气象产量、相对气象产量为目标变量构建随机森林产量预测模型，根据经验及多次试验，将RF算法的参数和分别设为500和15。以2010—2015年633组数据作为验证样本输入各个预测模型，结果如图4。从图中可以看出，单产模型的2达到0.71，MAE和RMSE分别达到1 213、1 387 kg/hm2，样本分布较为松散，预测结果整体上比实测值要低；而气象产量和相对气象产量的预测效果显著优于单产模型，趋势线与1:1线的交叉点均在0刻度附近，大部分样本聚集在1:1线周围，有较高的拟合度，决定系数2均达到0.8以上，气象产量的MAE和RMSE分别达到415、558 kg/hm2，相对气象产量的MAE和RMSE分别达到0.07和0.09，相较于单产模型表现出更小的偏差。

产量总体趋势是增长的，这与品种改良、技术进步以及田间管理等措施有关。在没有消除趋势产量的情况下，基于1990—2009年数据构建的随机森林单产模型中的最大值会较大概率低于后面的年份，导致预测结果整体偏低；气象产量和相对气象产量的拟合程度较高则说明二者均能较好地去除产量年际间生产技术水平的影响，且相对气象产量的趋势线与1:1线最为贴合，说明在气象差异的影响下，相对气象产量相较于气象产量更能突出空间差异造成的影响，利用随机森林能达到较好的预测效果。

注：*，P<0.05；**，P<0.01；下同。

2.2 不同特征变量类型对模型的影响分析

分别使用47个气象特征、3个空间特征以及使用全部特征变量作为特征集，相对气象产量作为目标变量，RF算法的参数保持不变设为500，分别设为13、1和15。利用2010—2015年河南省产量数据进行验证，结果见图5。由图可知，仅使用气象特征预测结果较差，趋势线较为平缓；仅使用空间特征预测精度虽然有所提高，但由于预测结果仅取决于地理位置，样本点沿1:1线呈水平分布，利用RF算法在相同地区不同的产量数据会被预测为相同的值，远离1:1线的样本点可以推断为受到了气象要素的影响；而在同时使用空间特征和气象特征对产量进行预测时，由图5c所示，大部分样本点聚集程度较高，相比前者预测结果表现出更小的偏差，相同地区不同的相对气象产量因为气象要素的加入更贴近于真值。可见，在构建随机森林对冬小麦产量进行预测时，需要考虑空间要素对产量造成的影响。

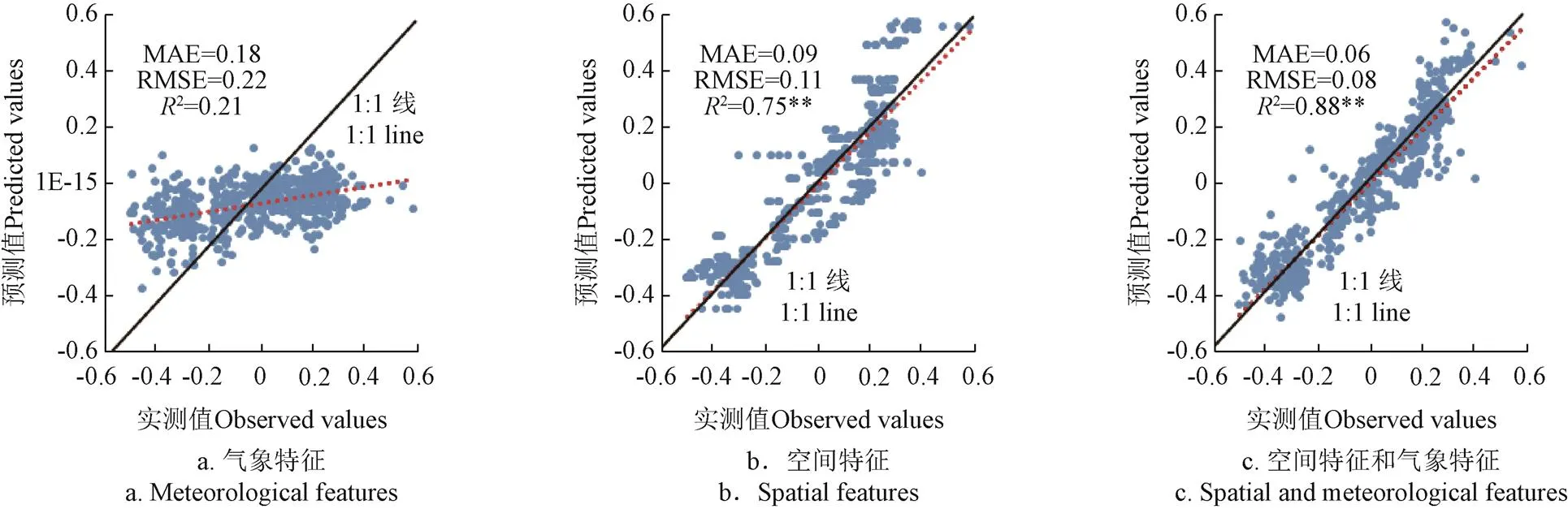
图5 不同特征变量RF预测的相对气象产量的结果对比

2.3 不同穗分化期对模型的影响分析

为探究不同时段的冬小麦预测精度，分别将小花分化前期等的气象要素和空间特征作为特征集，对相对气象产量进行建模，结果如图。由图可知，基于冬小麦小花分化后期以及抽穗开花期的估产精度比其他时期高，2达到0.8以上。小花分化期是决定穗数和粒数的关键时期，作物对气象变化敏感，而抽穗期是冬小麦将有机物从营养器官转移到籽粒的阶段，气象要素与小麦千粒质量密切相关，这2个穗分化期的气象要素对产量影响最大，故估产精度最高。药隔后期的产量预测值与实际值的偏差最大，这是由于相比其他时期，该时期内气象要素之间存在较强相关性，存在多重共线性，削弱了空间特征的影响所造成的。综上，利用小花分化后期和抽穗开花期的气象条件通过RF算法可达到较好的产量预测效果。

图6 不同穗分化期RF预测结果对比

2.4 模型误差空间分布

将模型参数和分别设为500和15，使用全部特征变量，以相对气象产量为目标变量构建随机森林模型，然后对2014和2015年河南省小麦种植区分别进行验证，结果如图7。根据河南省各县市统计数据[19]，冬小麦单产常年东南部偏高，西北部偏低。究其原因，主要是因为在纬度高的地区，太阳高度角比较小，存在斜射现象，单位面积的地表获得的太阳辐射少，作物物候期较晚，实际产量较低；纬度较低的区域物候期较早，实际产量较高。考虑到河南省地势基本上是西高东低，西部山区温度相对较低，不能满足冬小麦正常生长发育所需要的活动积温，对小麦高产稳产有一定影响。从图7中可以看出，相对气象产量的相对误差均在±0.2内，预测结果整体上呈现东南部偏低，西北部偏高的分布趋势。2014—2015年，西部地区的三门峡市、洛阳市和北部的安阳市冬小麦单产分别低于河南省平均产量26%～40%左右，而模型预测相对误差平均在0.15左右，东南部地区的商丘市、周口市和驻马店市的小麦单产分别高于全省平均产量的18%～22%左右，常年高于全省均值的20%左右，模型预测相对误差平均在-0.18左右。显然，模型预测结果在实际产量较低时易被高估，在实际产量较高时易被低估，这是由于RF算法预测结果为多棵决策树投票得到的结果所致，算法本身倾向于数据的平均状态[25]。

2.5 特征变量重要性分析

利用1990—2015年的冬小麦特征数据与相对气象产量分别进行基于RF的OOB重要性和相关性分析，按照OOB误差对特征变量进行由大到小排序，结果见表1。重要性排名前3为均为空间特征，依次为纬度（at）、高程（le）和经度（on），且他们的||也很显著，说明空间位置对相对气象产量的影响起着主导地位，决定了其本底数值。第4～7位分别为小花分化后期的平均温度（avg）小花分化前期的最低温（min）、拔节至抽穗期总时段的负积温（AT）和抽穗开花期的最高温度（max），代表4个不同的气象指标，平均温度代表了小麦基本的热量需求，最低温度、负积温和最高温度则分别代表了极端低温条件、持续低温累积、极端高温条件对小麦的胁迫影响，因为负积温主要是在初级累积，这个结果也反映了该地区初期易遭受晚霜冻害、后期易受干热风影响的气候特点，这与以往研究结果[26-27]相一致。

从||看，除了空间位置的重要性与||基本一致外，气象要素的重要性与||的关系没呈现出明显规律性。如各阶段最大气温日较差（T）的||在0.22～0.29之间，但其重要性并未体现出来，而各阶段平均气温（avg）的||更只有0.01～0.09，但小花分化后期的平均温度（avg）的重要性相对较为显著，表明单因素气象特征与相对气象产量的相关性不太具有意义。

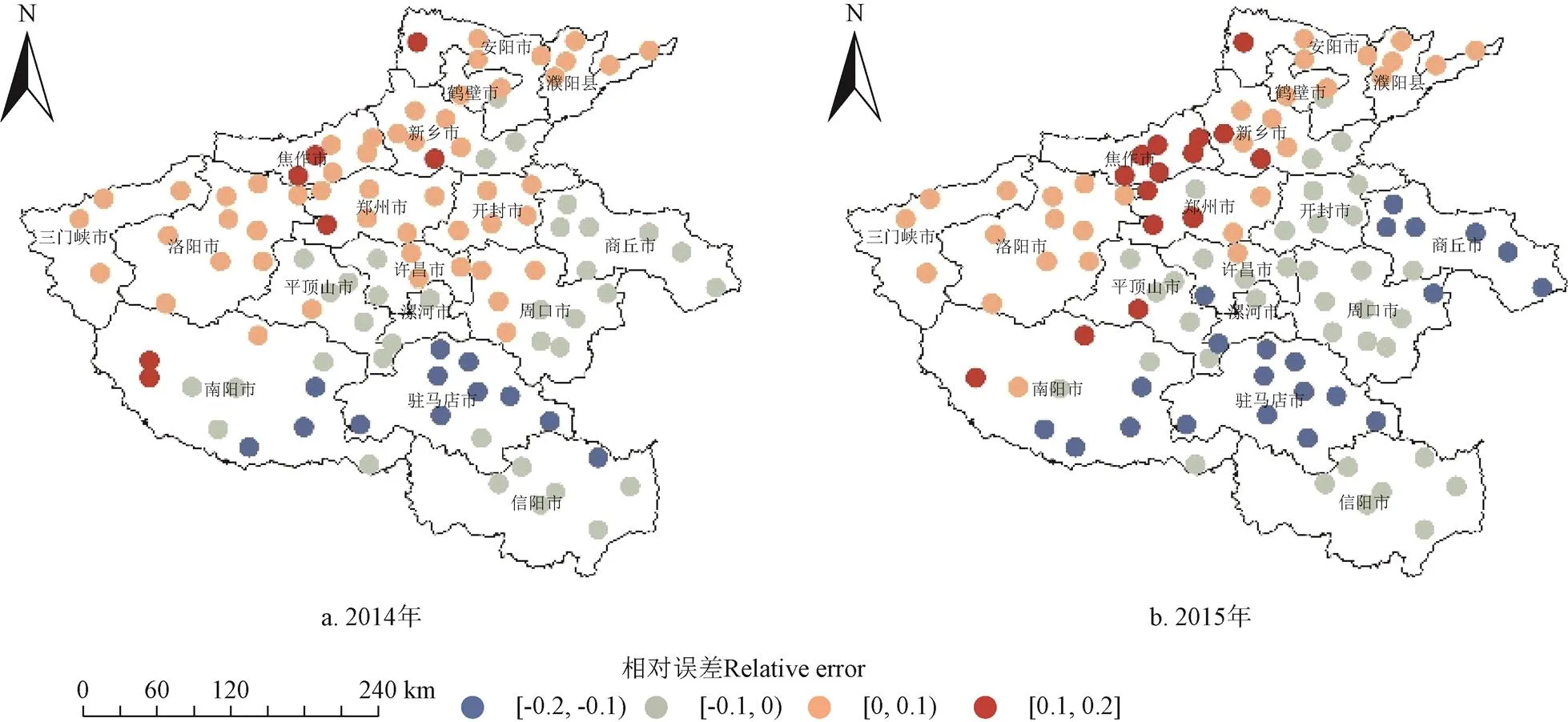
图7 2014—2015年河南省相对气象产量相对误差分布图

河南省是晚霜冻害发生较为频繁的地区[28]，国内学者多以最低气温作为该研究区的气象指标，张雪芬等[29]发现低温发生频率与产量之间相关性显著，但产量受诸多因素影响[30]，低温并不必然导致灾害发生，随着品种和耕作措施的改进，即使发生低温，后期仍可能获得丰产。这可解释了表1中气象特征重要性和相关性不一致的问题，利用单一气象指标建立回归分析，预测结果可能会存在较大偏差。随机森林重要性的概念反映的是多因素叠加作用下，该因素的影响程度，并将这种叠加效果在宏观层面体现出来，其重要优势之一是能处理具有多维特征的数据，并且不用做特征筛选，这有助于从更综合的层面上来分析多个因素的叠加影响[31]。

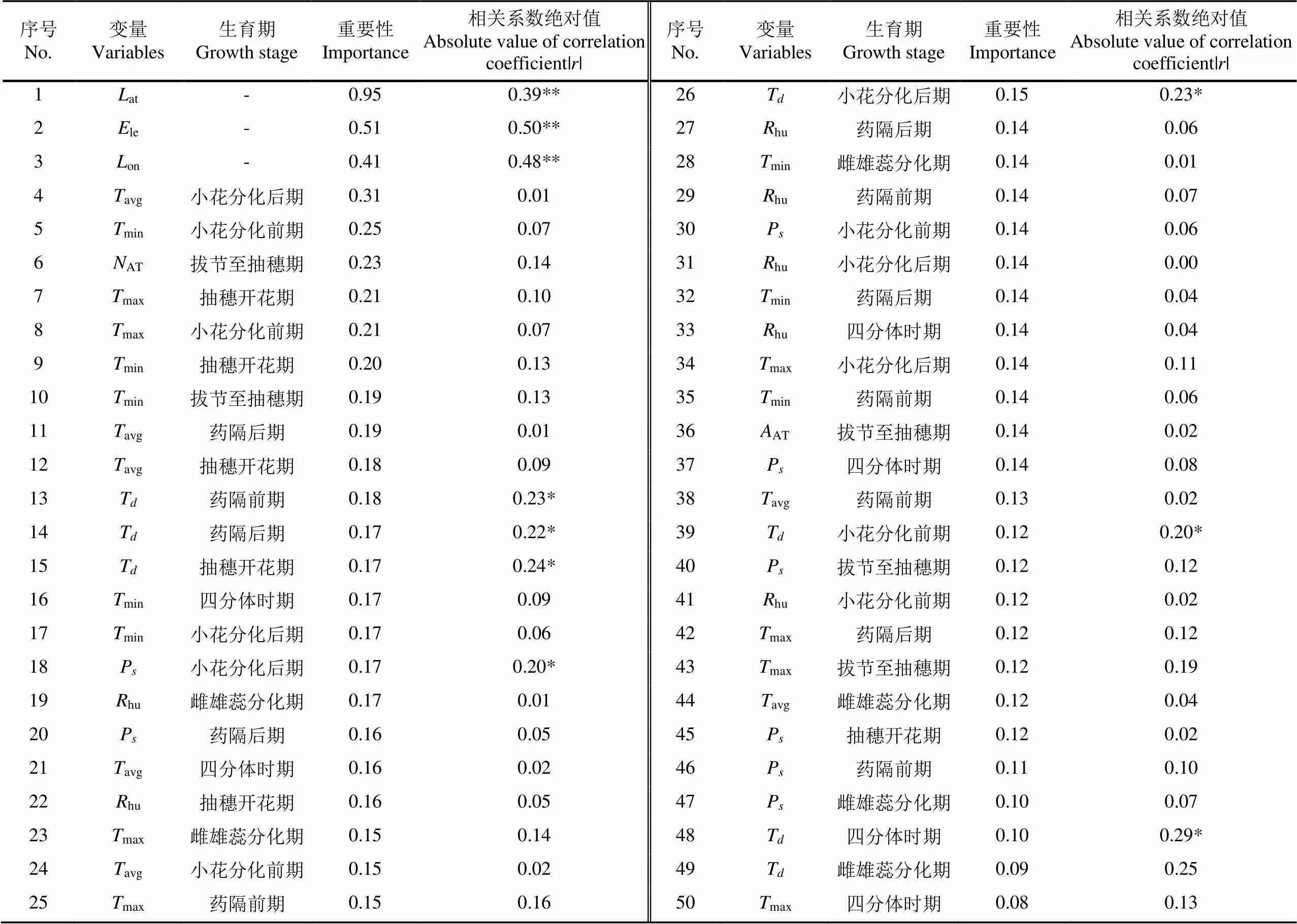
表1 特征变量重要性及变量与相对气象产量之间相关性分析

3 讨 论

受地势影响，河南省冬小麦种植面积常年东多西少，单产东南高西北低[19]，呈现显著的空间分布特征。空间位置主要影响作物所获得的积温和物候，但由于气象条件年际差异大以及样本时间周期不是很长，导致空间位置与气象环境因素之间的相关性较弱，因此在构建随机森林的过程中，不能仅考虑气象要素特征，空间差异性是需要考虑的重要因素。

理论上气象产量和相对气象产量仅受气象条件影响，但因它们的值不能直接通过测量获取，所以高度依赖于去趋势方法的选择。本文基于5a滑动平均方法对单产进行了去趋势而得到气象产量和相对气象产量，虽然可在一定程度上消除单产的年际影响，能突出气象要素对产量的影响，该方法具有一定的局限性，可以考虑其他去趋势方法，尽可能仅保留气象特征对产量的影响，减小影响因素的干扰。

在时间段划分方面，本文根据河南省平均拔节时间和平均抽穗时间，将该时段均匀划分，每年采用相同的时间节点作为小麦穗分化期的划分依据，但小麦穗分化进程受到温度、水分以及品种特性在内的诸多因素的影响[32-33]，因此，为了进一步提高模型的预测精度，可考虑气象变化的年际差异，更为准确地划分时间段。

由于总体样本数量偏少，灾害样本更少，本文未将灾害年和非灾害年分开建模，基于较少样本训练建立的模型可能会产生较大偏离。本文选用1990—2009年用于训练，2010—2015年用于验证，带有一定的主观性，但考虑到2010—2015年间，既有比较正常的样本，也有灾害样本，既有比较正常的年份，也有灾害年份，所以这段时间作为验证年份具有合理性。

4 结 论

基于地面观测气象数据、空间特征与冬小麦实际单产数据，利用随机森林算法对冬小麦产量进行了回归试验，对预测结果的空间分布状况进行了分析，并结合袋外数据重要性对产量影响因子进行了探讨。结果如下：

1）随机森林算法在预测产量上具有很大潜力，使用气象产量和相对气象产量作为目标变量建模的预测效果优于单产模型，相对气象产量的预测效果最优，其决定系数2达到0.84，平均绝对误差（mean absolute error，MAE）和均方根误差（root mean square error，RMSE）分别达到0.07和0.09左右。

2）空间特征在所构建的随机森林产量预测模型中起到了重要的作用，在此基础上增加气象特征可以使预测结果表现出更小的偏差，2达到0.88，MAE和RMSE分别达到0.06和0.08，且利用冬小麦小花分化期以及抽穗开花期的气象特征进行估产，精度要高于其他穗分化期，说明该时段环境的变化对最终产量造成的影响更大。

3）利用袋外数据变量重要性得出除了空间特征之外，冬小麦小花分化期的平均温度和最低温度、拔节至抽穗期间的负积温、抽穗开花期的最高温度4个气象指标对产量影响较大。

[1] Capa-Morocho M, Rodríguez-Fonseca Belén, Ruiz-Ramos M . Crop yield as a bioclimatic index of El Niño impact in Europe: Crop forecast implications[J]. Agricultural and Forest Meteorology, 2014, 198/199: 42－52.

[2] 王静，李新. 基于作物生长模型和多源数据的融合技术研究进展[J]. 遥感技术与应用，2015，30(2)：209－219. Wang Jing, Li Xin.Research progress of fusion technology based on crop growth model and multi-source data[J].Remote Sensing Technology and Application, 2015, 30(2): 209－219. (in Chinese with English abstract)

[3] 黄健熙，贾世灵，马鸿元，等. 基于WOFOST模型的中国主产区冬小麦生长过程动态模拟[J]. 农业工程学报，2017，33(10)：222－228. Huang Jianxi, Jia Shiling, Ma Hongyuan, et al. Dynamic simulation of growth process of winter wheat in main production areas of China based on WOFOST model[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(10): 222－228. (in Chinese with English abstract)

[4] Brown J N, Zvi H, Dean H, et al. Seasonal climate forecasts provide more definitive and accurate crop yield predictions[J]. Agricultural and Forest Meteorology, 2018, 260/261: 247－254.

[5] Basist A, Dinar A, Blankespoor B, et al. Use of satellite information on wetness and temperature for crop yield prediction and river resource planning[J]. Climate Smart Agriculture, 2018, 52: 77－104.

[6] Zhang S, Liu L. The potential of the MERIS Terrestrial Chlorophyll Index for crop yield prediction[J]. Remote Sensing Letters, 2014, 5(8):10.

[7] 黎锐，李存军，徐新刚，等. 基于支持向量回归（SVR）和多时相遥感数据的冬小麦估产[J]. 农业工程学报，2009，25(7)：114－117. Li Rui, Li Cunjun, Xu Xingang, et al. Winter wheat yieldestimation based on suport vector machine regression andmulti-temporal remote sensing data[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2009, 25(7): 114－117. (in Chinese with English abstract)

[8] Zai Songmei, Jia Yanhui, Wen Ji, et al. Study on grain yield prediction of irrigation district based on least squares support vector machine[J]. Agricultural Science and Technology, 2009, 10(6): 1－3, 6.

[9] 姜新. 河南省粮食产量影响因素和预测方法研究[J]. 中国农学通报，2019，35(1)：154－158. Jiang Xin. Study on the factors affecting grain yield and forecasting methods in henan province[J]. Chinese Agricultural Science Bulletin, 2019, 35(1): 154－158. (in Chinese with English abstract)

[10] Pandey A, Mishra A. Application of artificial neural networks in yield prediction of potato crop[J]. Russian Agricultural Sciences, 2017, 43(3): 266－272.

[11] Kaul M, Hill R L, Walthall C . Artificial neural networks for corn and soybean yield prediction[J]. Agricultural Systems, 2005, 85(1): 1－18.

[12] Uno Y, Prasher S O, Lacroix R, et al. Artificial neural networks to predict corn yield from compact airborne spectrographic imager data[J]. Computer and Electronics in Agriculture, 2005, 47(2): 149－161.

[13] Breiman L. Random forests[J]. Machine Learning, 2001, 45(1): 5－32.

[14] 方匡南，吴见彬. 随机森林方法研究综述[J]. 统计与信息论坛，2011，26(3)：32－38. Fang Kuangnan, Wu Jianbin. A review of random forest method research[J]. Statistics and Information Forum, 2011, 26(3): 32－38.

[15] Anna Chlingaryan, Salah Sukkarieh, Brett Whelan. Machine learning approaches for crop yield prediction and nitrogen status estimation in precision agriculture: A review[J]. Computers and Electronics in Agriculture, 2018, 151: 61－69.

[16] Dhivya Elavarasan, Durai Raj Vincent, Vishal Sharma, et al. Forecasting yield by integrating agrarian factors and machine learning models: A survey[J]. Computers and Electronics in Agriculture, 2018, 155: 257－282.

[17] Everingham Y, Sexton J, Skocaj D, et al. Accurate prediction of sugarcane yield using a random forest algorithm[J]. Agronomy for Sustainable Development, 2016, 36(2): 1－9.

[18] Tulbure M G, Wimberly M C, Boe A, et al. Climatic and genetic controls of yields of switchgrass, a model bioenergy species[J]. Agriculture Ecosystems and Environment, 2012, 146(1): 121－129.

[19] 河南省统计局. 河南农村统计年鉴1990－2015[M]. 北京：中国统计出版社，2016.

[20] 王绍中，田云峰，郭天财，等. 河南小麦栽培学[M]. 北京：中国统计出版社，2011.

[21] 崔金梅，郭天财. 小麦的穗[M]. 北京：中国农业出版社，2006.

[22] 房世波. 分离趋势产量和气候产量的方法探讨[J].自然灾害学报，2011，20(6)：13－18. Fang Shibo. Discussion on methods of separating trend yield and climate yield[J]. Journal of Natural Disasters, 2011, 20(6): 13－18. (in Chinese with English abstract)

[23] Jamieson P D, Porter J R, Wilson D R. A test of the computer simulation model ARCWHEAT1 on wheat crops grown in New Zealand[J]. Field Crops Research, 1991, 27(4): 337－350.

[24] Zhu Y, Li Y, Feng W, et al. Monitoring leaf nitrogen in wheat using canopy reflectance spectra[J]. Canadian Journal of Plant Science, 2006, 86(4): 1037－1046.

[25] Zhou Zhihua, Ji Feng. Deep forest: Towards an alternative to deep neural networks[J]. Machine Learning, 2017, 497: 3553－3559.

[26] 张荣荣，宁晓菊，秦耀辰，等. 1980年以来河南省主要粮食作物产量对气象变化的敏感性分析[J]. 资源科学，2018，40(1)：137－149. Zhang Rongrong, Ning Xiaoju, Qin Yaochen, et al. Sensitivity analysis of main grain crop yields to climate change in Henan Province since 1980[J]. Resources Science, 2018, 40(1): 137－149. (in Chinese with English abstract)

[27] 成林，李彤霄，刘荣花. 主要生育期气象变化对河南省冬小麦生长及产量的影响[J]. 中国生态农业学报，2017，25(6)：931－940. Cheng Lin, Li Tongxiao, Liu Ronghua. Effects of climate change during main growth period on winter wheat growth and yield in Henan Province[J].Chinese Journal of Eco-Agriculture, 2017, 25(6): 931－940. (in Chinese with English abstract)

[28] 冯玉香，何维勋，孙忠富，等. 我国冬小麦霜冻害的气候分析[J]. 作物学报，1999，25(3)：335－340. Feng Yuxiang, He Weixun, Sun Zhongfu, et al. Climatological study onfrost damage of winter wheat in China[J]. Acta Agronomy Sinica, 1999, 25(3): 335－340. (in Chinese with English abstract)

[29] 张雪芬，郑有飞，王春乙，等. 冬小麦晚霜冻害时空分布与多时间尺度变化规律分析[J]. 气象学报，2009，67(2)：321－330. Zhang Xuefeng, Zheng Youfei, Wang Chunyi, et al. Spatial-temporal distribution and multiple-temporal scale variationanalyses of winter wheat late freezing injury[J].Acta Meteorologica Sinica, 2009, 67(2): 321－330. (in Chinese with English abstract)

[30] 朱虹晖，武永峰，宋吉青，等. 基于多因子关联的冬小麦晚霜冻害分析：以河南省为例[J]. 中国农业气象，2018，39(1)：59－68. Zhu Honghui, Wu Yongfeng, Song Jiqing, et al. Analysis of winter frost damage of winter wheat based on multi-factor correlation: A case study of Henan Province[J]. Chinese Journal of Agricultural Meteorology, 2018, 39(1): 59－68. (in Chinese with English abstract)

[31] Gislason P, Benediktsson J. Random forests for land cover classification[J]. Pattern Recognition Letters, 2006, 27(4): 294－300.

[32] Mo X , Liu S , Lin Z , et al. Prediction of crop yield, water consumption and water use efficiency with a SVAT-crop growth model using remotely sensed data on the North China Plain[J]. Ecological Modelling, 2005, 183(2/3):301-322.

[33] Krupnik T J, Ahmed Z U, Timsina J, et al. Untangling crop management and environmental influences on wheat yield variability in Bangladesh: An application of non-parametric approaches[J].Agricultural Systems, 2015, 139: 166－179.

Early prediction of winter wheat yield with long time series meteorological data and random forest method

Liu Junming1,3, He Xiaotong1,3, Wang Pengxin2,3, Huang Jianxi1

(1.,,100083,2.,,100083,3.,,100083,)

Early prediction of winter wheat yield is of great significance for the formulation of precise management decisions for the whole growth period of winter wheat. The yield of winter wheat is affected by production technology level and climatic conditions. This study analyzed the feasibility of early prediction of winter wheat yield with long time series meteorological data and random forest method in Henan Province. Winter wheat was planted in a total of 106 counties (cities) in Henan province. Based on the ground observation meteorological data and the winter wheat statistical yield data from the year of 1990 to 2015, we extracted 47 climatic factors such as temperature, humidity and precipitation in different growth stages from wheat jointing to heading stage, and 3 spatial factors of latitude, longitude and elevation. A total of 50 parameters were used as a set of feature variables. The actual yield, meteorological yield and relative meteorological yield were used as the target variables respectively, and a random forest yield prediction model with multiple variables was constructed. The data from the year of 1990 to 2009 were used as training samples to construct the model and the forests constructed were validated with data from the year of 2010 to 2015. The yield impact factors were analyzed by combining the data importance results outside the bag. The results showed that: 1) The prediction results by using meteorological yield and relative meteorological yield as the target variables were better than the yield model. For the meteorological yield and relative meteorological yield models, the values of determination coefficient2were both above 0.8, the values of mean absolute error (MAE) and root mean square error (RMSE) of meteorological yield were 415 and 558 kg/hm2, respectively, and the values of MAE and RMSE of relative meteorological yield were 0.07 and 0.09, respectively; 2) The spatial characteristics played an important role in the improving the random forest yield model. However, if the model included only spatial parameters, the predicted values were horizontally distributed along 1:1 line and the different yields in the same region by using random forest algorithm were predicted as the same values. The values far from 1:1 line might be affected by meteorological factors. Therefore, on this basis, adding meteorological features improved the prediction accuracy with smaller deviations, higher2(0.88), and smaller MAE and RMSE (0.06 and 0.08). 3) The model prediction was also affected by crop growing stages. The accuracy based on the meteorological features of winter wheat florets differentiation and heading and flowering stage was higher than the other spike differentiation periods, indicating that the environmental changes during this period have a greater impact on the final yield; The predicted results at the late drug interval had the larger deviation from the actual yield. It was because the meteorological factors had strong correlation and it weakened the impacts of spatial characteristics. 4) Based on the importance of outside the bag data, In the meteorological features, the average temperature and minimum temperature of winter wheat floret differentiation period, the spatial characteristics parameters were important. In addition, the negative accumulated temperature from the jointing to heading stage, and the maximum temperature at heading and flowering stage had great influence on yield. During the model establishment, we didn’t differentiate disaster from non-disaster year because the sample sizes were small. However, during the model validation, the data were from both normal and disaster years, which could ensure the reliability of the prediction model. Thus, the winter wheat yield prediction based on random forest should consider both spatial and meteorological characteristics parameters. The results of this study provide new ideas and methods for early prediction of winter wheat yield.

models; temperature; random forest;yield prediction; winter wheat

2018-09-20

2019-02-28

国家自然科学基金项目（41471342）

刘峻明，副教授，博士，主要从事地理信息系统和定量遥感研究。Email：liujunming2000@163.com

10.11975/j.issn.1002-6819.2019.06.019

S127；S512.1+1

A

1002-6819(2019)-06-0158-09

刘峻明，和晓彤，王鹏新，黄健熙. 长时间序列气象数据结合随机森林法早期预测冬小麦产量[J]. 农业工程学报，2019，35(6)：158－166. doi：10.11975/j.issn.1002-6819.2019.06.019 http://www.tcsae.org

Liu Junming He Xiaotong Wang Pengxin, Huang Jianxi. Early prediction of winter wheat yield with long time series meteorological data and random forest method[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(6): 158－166. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2019.06.019 http://www.tcsae.org