四足机器人腿部并联机构末端位置误差分析与验证

王晓磊，金振林，李晓丹



四足机器人腿部并联机构末端位置误差分析与验证

王晓磊1,2，金振林1,3※，李晓丹2

（1.燕山大学机械工程学院，秦皇岛 066004；2. 辽宁工业大学机械工程与自动化学院，锦州 121001； 3. 上海交通大学机械系统与振动国家重点实验室，上海 200240）

机器人；模型；机构；误差灵敏度；位置精度

0 引 言

1 四足机器人腿部机构

该四足机器人由4条相同的机械腿组成，如图1所示。每条机械腿均由RPR（R为转动副，P移动副）机构和2-DOF（degree of freedom）平面并联机构组成，由3个伺服液压缸驱动，可实现迈步长度可达1 000 mm，抬腿高度可达400 mm。2-DOF并联机构由5杆机构与双菱形行程放大机构组合实现足端的迈步；RPR机构驱动2-DOF并联机构整体带动足端侧摆，实现机械腿的侧向解耦。该仿生机器人的腿部机构的优点是液压缸活塞杆只需移动很小的距离，就能获得很大的工作空间，可实现快速、大步伐行走；同时采用串并混联的腿部结构，较传统的串联机械腿相比，具有较大的承载能力；采用液压伺服技术，使四足仿生机器人的动态特性力及承载能力更好，适合用于高负载的应用场合[20]。由于该腿部机构由串并混联机构组成，串联机构相对简单，所以本文重点对并联机构进行分析。

a. 虚拟样机模型a. Virtual prototype modelb. 腿部机构模型b. Leg mechanism model

1.伺服液压缸 2.架体 3.双菱形机构 4.缓冲弹簧 5.足端

1.Servo hydraulic cylinder 2.Frame 3.Double diamond mechanism 4.Buffer spring 5.Foot end

图1 虚拟样机与腿部机构模型

Fig.1 Virtual prototype and leg mechanism model

2 平面并联机构坐标系建立及位置分析

平面并联机构坐标系的建立及其结构简图如图2所示。以为原点建立参考坐标系，以为原点建立动坐标系。其中，轴沿矢量方向，轴垂直轴向上；轴沿矢量方向，轴垂直轴向左。

结合图2，根据结构尺寸约束可得到：

参考点的位置坐标为:

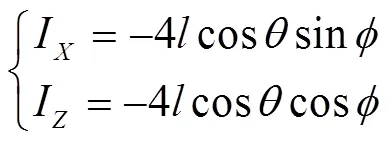
由于为一个矢量闭环，并将其分解成沿、轴的2个分量：

同理，矢量为：

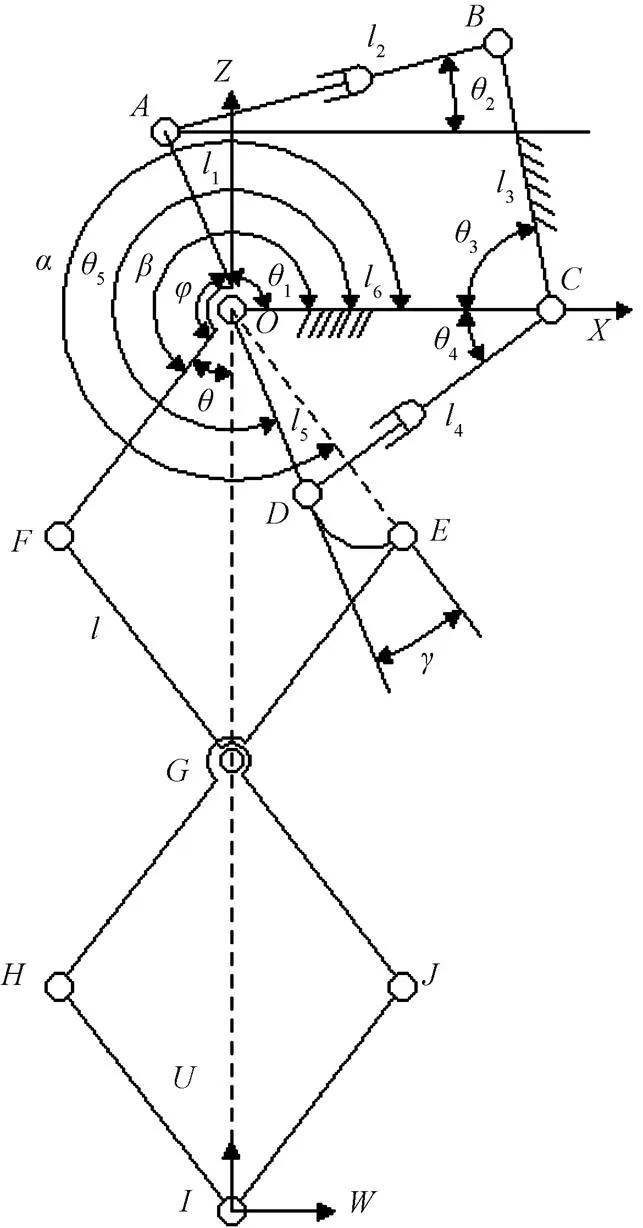
注：A、B、C、D、E、F、G、H、I、J表示机构各转动副的中心点。主要几何参数mm,mm，mm，mm，mm，mm；为双菱形OFGE和GHIJ边长，mm；为OE与X轴夹角，(°)；为OD与OE夹角，(°)；为OF与X轴的夹角，(°)；为OA与OF夹角，(°)；为OF与OG夹角，(°)；为OA与X轴夹角，(°)；为AB与X轴夹角，(°)；为BC与X轴夹角，(°)；为CD与X轴夹角，(o)；为OE与X轴夹角，(°)。XOZ和UIW分别为参考坐标系和动坐标系。

3 末端位置误差模型的建立

该平面并联机构是行程放大机构，各构件微小的制造误差就会使机构末端位置产生一个很大的误差，所以本文重点分析末端位置误差与机构中各构件制造误差的映射关系。

对式（1）、式（2）求全微分，合并整理得

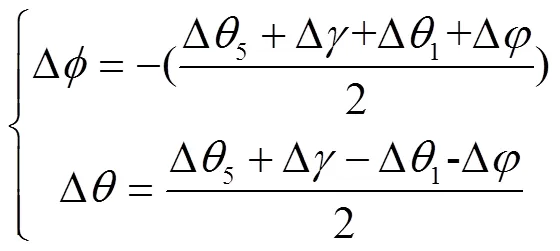
对式（3）求全微分

将式（6）、式（7）合并可得

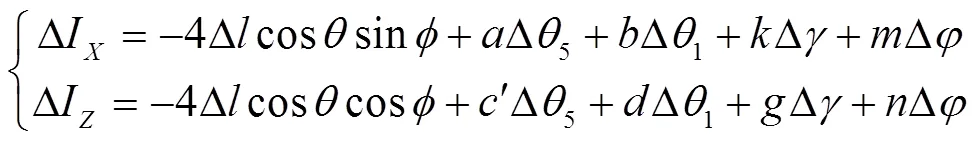
对式（4）取全微分，整理得

对式（5）取全微分，整理得

将式（9）、式（10）带入式（8）中得

4 末端位置误差灵敏度分析

误差灵敏度分析有助于确定误差源对定位精度的影响程度[21-22]，可以为腿部机构构件的加工与装配提供理论依据。

4.1 位置误差灵敏度模型

位置误差灵敏度模型[23]可由式（11）两端取模得出：

4.2 位置误差灵敏度分析

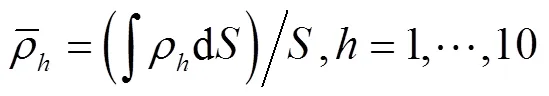
注：∆l、∆li(i=1,2,3,4,5,6)表示各杆长度制造误差；，，表示角度、、的制造误差。

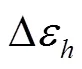
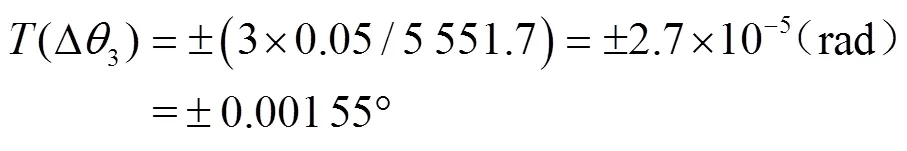
表1 各构件的允许制造公差范围计算结果

5 末端位置精度预估与验证

5.1 位置精度预估

由于机构的误差映射矩阵与机构所处的位形有关，在不同位形时，机构末端在工作空间不同点的误差值也是不同的。为了揭示出末端位置误差在工作空间的分布规律，需要对末端位置精度进行预估。

表2 各构件实测制造误差

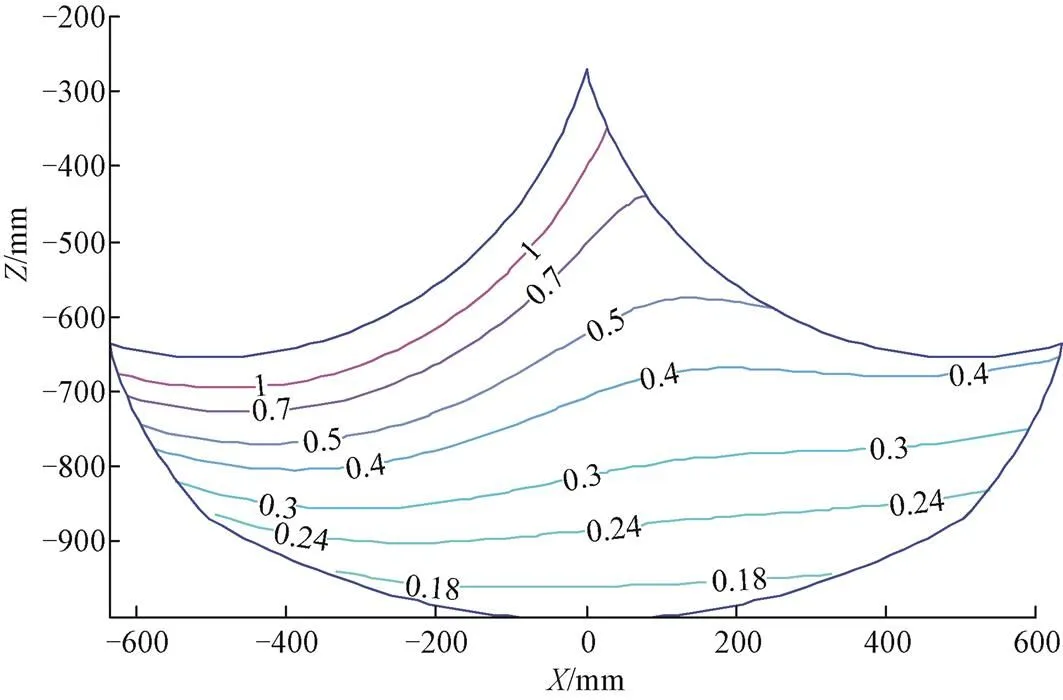
注：等高线上的数字为位置精度预估值，mm。

从图4中可以看出，位于工作空间中下部的位置误差在0.18～0.3 mm范围内，精度较好；位于工作空间中上部位置误差在0.4～1 mm范围内，而且越处于上部的位置精度越差，其中左上及顶部误差为1 mm。因此，四足机器人在执行较为精确的任务时，足端着地点的轨迹可以规划在工作空间中下部的区域，提高足端定位精度。

5.2 实例验证

图6 位姿点测试

表3 位姿点位置误差测试结果

6 结 论

1）建立2-DOF并联机构的位置模型，建立了误差源与末端定位精度的误差传递模型，确定了影响末端位置精度的误差源。

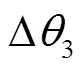
3）通过三坐标测量仪测出各构件的制造误差，在工作空间内进行了末端位置的精度预估。从工作空间内的精度分布可知，位于工作空间中下部位置误差在0.18～0.3 mm范围内，精度较高；位于工作空间中上部位置误差在0.4～1 mm范围内，精度较差，而且越处于上部位置精度越差，其中左上及顶部最差，位置误差为1 mm。通过样机测试试验，得出实际精度值与理论精度预估值最大误差绝对值为0.003 8 mm，最小误差绝对值为0.001 5 mm，与理论预估值均相差较小，验证了误差传递模型、精度预估的正确性，为该类仿生机器人的运动学标定、误差补偿及执行精确任务时的轨迹规划奠定了基础；也验证该方法确定构件制造误差的有效性。

[1] 王友渔，赵兴玉，黄田，等. 可重构混联机械手TriVariant与Tricept的静动态特性预估与比较[J]. 天津大学学报，2007，40(6)：41－45. Wang Youyu, Zhao Xingyu, Huang Tian, et al. Estimation and comparison of static and dynamic performance of two reconfigurable hybrid robots-the trivariant and the tricept[J]. Journal of Tianjin University, 2007, 40(6): 41－45. (inChinese with English abstract)

[2] 荣誉，金振林，曲梦可. 三自由度并联机械腿静力学分析与优化[J]. 农业工程学报，2012，28(20)：41－49. Rong Yu, Jin Zhenlin, Qu Mengke. Statics analysis and optimal design of 3-DOF parallel mechanical leg[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012, 28(20): 41－49. (in Chinese with English abstract)

[3] 张金柱，金振林，张天浩. 并联驱动机械腿运动学静力学性能评价及几何参数设计[J]. 农业工程学报，2017，33(21)：61－69. Zhang Jinzhu, Jin Zhenlin, Zhang Tianhao. Kinematic/static performance evaluation and geometric parameter design of parallel-driving leg mechanism[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(21): 61－69. (in Chinese with English abstract)

[4] 牛建业，王洪波，史洪敏，等. 变自由度轮足复合机器人轨迹规划验证及步态研究[J]. 农业工程学报，2017，33(23)：38－47. Niu Jianye, Wang Hongbo, Shi Hongmin, et al. Trajectory planning verification and gait analysis of wheel-legged hybrid robot with variable degree of freedom[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33 (23): 38－47. (in Chinese with English abstract)

[5] 曲梦可，王洪波，荣誉. 轮腿混合四足机器人六自由度并联机械腿设计[J]. 农业工程学报，2017，33(11)：29-37. Qu Mengke, Wang Hongbo, Rong Yu. Design of 6-DOF parallel mechanical leg of wheel-leg hybrid quadruped robot[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(11): 29-37. (in Chinese with English abstract)

[6] Merlet J P. Jacobian, manipulability, condition number, and accuracy of parallel robots[J]. Journal of Mechanical Design, 2006, 128(1): 199－206.

[7] Zheng Defeng, Wang Xiangzhao, Li Zhongliang. Accuracy analysis of parallel plate interferometer for angular displacement measurement[J]. Optics&Laser Technology, 2008, 40(1): 6－12.

[8] 谢福贵，刘辛军，陈禹臻. 一种新型虚拟中心并联机构的误差灵敏度分析[J]. 机械工程学报，2013，49(17)：85－91. Xie Fugui, Liu Xinjun, Chen Yuzhen. Error sensitivity analysis of novel virtual center mechanism with parallel kinematics[J]. Journal of Mechanical Engineering, 2013, 49(17): 85－91. (in Chinese with English Abstract)

[9] 张立杰，李永泉. 球面2-DOF冗余驱动并联机器人机构误差分析[J]. 机械工程学报，2013，49(7)：148－154. Zhang Lijie, Li Yongquan. Error analysis of spherical 2-DOF parallel manipulator with actuation redundancy[J]. Journal of Mechanical Engineering, 2013, 49(7): 148－154. (in Chinese with English Abstract)

[10] 李永泉，张立杰，郭志民，等. 基于D-H矩阵的球面5R并联机构误差建模及灵敏度分析[J]. 中国机械工程，2012，23(12)：1470－1474. Li Yongquan, Zhang Lijie, Guo Zhimin, et al. Error modeling and sensitivity analysis of spherical 5R parallel manipulator based on D-H matrix[J]. Chinese Mechanical Engineering, 2012, 23(12): 1470－1474. (in Chinese with English Abstract)

[11] 牛亚雯，温淑鸿，冯志友. 基于正交设计法的2UPS-RPU并联机构精度综合[J]. 机械科学与技术，2015，34(7)：997－1001. Niu Yawen, Wen Shuhong, Feng Zhiyou. Accuracy synthesis of 2UPS-RPU parallel manipulator based on orthogonal design[J]. Mechanical Science and Technology for Aerospace Engineering, 2015, 34(7): 997－1001. (in Chinese with English Abstract)

[12] Li Ruiqin, Yang Bin. Error modeling of 3-RSR parallel robot based on D-H transformation matrix[J]. Journal of Measurement Science and Instrumentation, 2014(3): 53－59.

[13] Huang T, Whitehouse D J, Chetwynd D G. A unified error model for tolerance design, assembly and error compensation of 3-DOF parallel kinematic machines with parallelogram struts[J]. Annals of CIRP, 2002, 5l(1): 299－303.

[14] Soons J A. Error analysis of a hexapod machine tool[J]. Laser Metrology and Machine Performance, 1997(3): 346－358.

[15] Chaker A, Mlika A, Laribi M A, et al. Accuracy analysis of non-overconstrained spherical parallel manipulators[J]. European Journal of Mechanics- A/Solids, 2014(47): 362－372.

[16] Chebbi A H, Affi Z, Romdhane L. Prediction of the pose errors produced by joints clearance for a 3-UPU parallel robot[J]. Mechanism & Machine Theory, 2009, 44(9): 1768－1783.

[17] Cui H, Zhu Z, Gan Z, et al. Kinematic analysis and error modeling of TAU parallel robot[J]. Robotics and Computer-Integrated Manufacturing, 2005, 21(6): 497－505.

[18] 孙通帅. 球面并联仿生髋关节误差模型分析及运动学实验研究[D]. 秦皇岛：燕山大学，2017. Sun Tongshuai. Error Analysis and Kinematic Experimental Study on the Bbionic Hip Joint with Spherical Parallel Manipulator[D]. Qinhuangdao: Yanshan University, 2017. (in Chinese with English Abstract)

[19] 荣誉，刘双勇，韩勇，等. 六足制孔机器人三自由度并联机械腿的误差模型及验证[J]. 农业工程学报，2016，32(15)：18－25. Rong Yu, Liu Shuangyong, Han Yong, et al. Error model and verification of three degrees of freedom parallel mechanical leg on hexapod drilling robot[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(15): 18－25. (in Chinese with English Abstract)

[20] 罗庆生，罗霄. 仿生四足机器人技术[M]. 北京：北京理工大学出版社. 2016.

[21] 洪振宇，梅江平，赵学满. 可重构混联机械手：TriVariant的误差建模与灵敏度分析[J]. 机械工程学报，2006，42(12)：65－69.Hong Zhenyu, Mei Jiangping, Zhao Xueman. Error modeling and sensitivity analysis of reconfigurable hybrid robot module TriVariant[J]. Journal of Mechanical Engineering, 2006, 42(12): 65－69. (in Chinese with English Abstract)

[22] 李铁民，郑浩峻，汪劲松，等. 并联机床不同位形下的运动精度评价指标[J]. 机械工程学报，2002，38(9)：101－105. Li Tiemin, Zheng Haojun, Wang Jinsong, et al. Precision measures for various configurations of parallel kinematic machine tools[J]. Journal of Mechanical Engineering, 2002, 38(9): 101－105. (in Chinese with English Abstract)

[23] 黄田，李亚，李思维. 一种三自由度并联机构几何误差建模、灵敏度分析及装配工艺设计[J]. 中国科学：E辑，2002，32(5)：628－635. Huang Tian, Li Ya, Li Siwei. Criteria for conceptual design of reconfigurable PKM modules theory and Application[J]. Science in China: Ser. E, 2002, 32(5):628－635. (in Chinese with English Abstract)

[24] 宋黎，杨坚，曹惟庆. 用蒙特卡洛法进行平面连杆机构的运动误差综合[J]. 机械科学与技术，1997(3)：107－110.Song Li, Yang Jian, Cao Weiqing. The motion error synthesis of planar likages through Monte Carlo method[J]. Mechanical Science and Technology for Aerospace Engineering, 1997(3): 107－110. (in Chinese with English Abstract)

[25] 曾宪菁，黄田，曾子亚. 3-RRR型数控回转台的精度分析[J].机械工程学报，2001，37(11)：42－45. Zeng Xianjing, Huang Tian, Zeng Ziya. Accuracy analysys of the 3-RRR NC swivel work table[J]. Chinese Journal of Mechanical Engineering, 2001, 37(11): 42－45. (in Chinese with English Abstract)

[26] 甘永立. 几何量公差与检测[M]. 上海：上海科学技术出版社，2013.

Analysis and verification of terminal position error of leg parallel mechanism of quadruped robot

Wang Xiaolei1,2, Jin Zhenlin1,3※, Li Xiaodan2

(1,,066004,; 2.,,121001,; 3.,,200240,

robots; models; mechanism; error sensitivity; positional accuracy

2018-09-28

2019-01-20

国家高技术研究发展计划（863计划）项目（2011AA040901）；机械系统与振动国家重点实验室课题资助项目（ MSV201506）；辽宁省高等学校科学技术研究项目（JL201615402）

王晓磊，副教授，博士生，主要研究方向为并联机构的理论及应用。Email：wxlgxy@126.com

金振林，教授、博士生导师，主要研究方向为并联机器人技术及应用。Email：zljin@ysu.edu.cn

10.11975/j.issn.1002-6819.2019.06.005

TH112

A

1002-6819(2019)-06-0039-08

王晓磊，金振林，李晓丹. 四足机器人腿部并联机构末端位置误差分析与验证[J]. 农业工程学报，2019，35(6)：39－46. doi：10.11975/j.issn.1002-6819.2019.06.005 http://www.tcsae.org

Wang Xiaolei, Jin Zhenlin, Li Xiaodan. Analysis and verification of terminal position error of leg parallel mechanism of quadruped robot[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(6): 39－46. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2019.06.005 http://www.tcsae.org