基于改进迟滞阻尼模型的混合结构抗震分析SRSS法

孙攀旭，杨红,b，刘庆林

(1. 重庆大学 a.土木工程学院；b.山地城镇建设与新技术教育部重点实验室，重庆 400045； 2. 深圳信息职业技术学院 交通与环境学院，广东 深圳 518172)

混合结构的地震响应计算方法与单一材料结构采用的常用方法不同。由于不同材料的阻尼比不同，混合结构的阻尼矩阵并不与质量矩阵或刚度矩阵保持比例关系，故混合结构无法直接采用基于粘性阻尼模型的实模态叠加法，抗震计算时也无法直接采用SRSS法。

目前，常用的阻尼模型为粘性阻尼模型和复阻尼模型[1]。对于混合结构，选择结构的重要振型，可得到相应的Rayleigh阻尼矩阵，进而实现模态叠加法[2-4]，但其结果不具有唯一性，高阶振型地震作用效应亦偏小[5]；采用等效阻尼比的思路，将阻尼矩阵等价为比例矩阵，同样可实现模态叠加法[6-7]，但计算出局部结构的地震效应偏小或偏大[8]；汪梦甫[9]、Neugebauer等[10-11]利用状态空间法，提出了基于粘性阻尼模型的复模态叠加法，但矩阵维度增加了一倍，计算量较大；刘庆林等[12]基于复阻尼模型的复模态叠加法可直接适用于混合结构，但计算较为复杂，且直接剔除复阻尼运动方程通解中发散项的做法存在理论缺陷[13]。Wang[14]采用Rayleigh阻尼矩阵等效复阻尼矩阵，Reggio等[15]将Maxwell-Wiechert本构模型等效于复阻尼本构模型，进而解决了发散问题，但上述方法得到的计算结果与复阻尼理论存在一定的误差。迟滞阻尼模型计算结果唯一，且克服了粘性阻尼模型中每周期耗散能量与外激励频率相关的缺点。同时，迟滞阻尼模型的时域计算结果稳定收敛，避免了复阻尼模型的发散现象[16]。

迟滞阻尼模型克服了粘性阻尼模型和复阻尼模型的缺陷，但不满足能量守恒的原则。本文利用结构每周期耗散能量与阻尼做功相等的特性，对迟滞阻尼模型的阻尼系数进行修正，得到改进迟滞阻尼模型，并提出了对应的混合结构模态叠加法。同时，分析改进迟滞阻尼模型的反应谱特点，计算最不利地震作用效应组合，并提出了基于改进迟滞阻尼模型的混合结构抗震分析SRSS法。

1 基于改进迟滞阻尼模型的SRSS法

1.1 改进迟滞阻尼模型

迟滞阻尼模型假定阻尼力与结构的位移大小成正比，与结构的速度方向相反[16-17]。单自由度体系的迟滞阻尼运动方程为

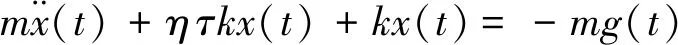
(1)

式中：m为质量；k为刚度；η为损耗因子，即η=2ξ[12]，ξ为阻尼比；g(t)为地震加速度。

(2)

设单自由度系统响应x=Xsinθt，一个振动周期内结构的耗散能量为

ΔE=πηkX2

(3)

一个振动周期内阻尼力做的功为

ΔW=-2ηkX2

(4)

由式(3)和式(4)可知，阻尼力做功与结构每周期耗散能量的大小不相等，需要对迟滞阻尼模型进行修正。定义迟滞阻尼模型下，单自由度体系的阻尼力为

fd=-λτkx(t)

(5)

式中：λ为阻尼系数。

由式(5)计算出每周期阻尼力做功为

ΔW=-2λkX2

(6)

利用每周期耗散能量与阻尼力做功大小相等，得

2λkX2=πηkX2

(7)

进一步计算出阻尼系数为

(8)

从而得到改进的迟滞阻尼运动方程为

(9)

1.2 基于迟滞阻尼模型的混合结构抗震分析SRSS法

改进迟滞阻尼模型下阻尼力为

(10)

由式(10)可得到改进迟滞阻尼模型的阻尼力-位移变化曲线(见图1)，阻尼力不随位移的变化而连续变化，因此，改进迟滞阻尼系统不再保持整体线性特征，而是具有局部非线性特征，导致多自由体系不能直接采用模态叠加法。

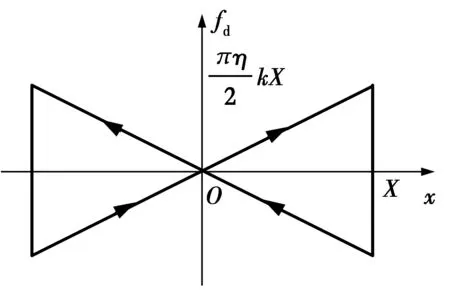
图1 阻尼力位移变化曲线Fig.1 The change curve between damping

对于混合结构，多自由度体系的改进迟滞阻尼运动方程为

(11)

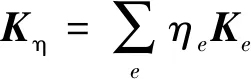
(12)

(13)

(14)

式(14)对应的齐次方程为

(15)

由式(15)可计算出对应的自振频率和特征向量，采用改进迟滞阻尼模型时，Kf可视为结构的动态刚度矩阵，结构的振动过程将是刚度不断变化的过程。由式(15)可知，方程的特征值和特征向量不仅与结构的质量、刚度和阻尼有关，还与运动过程中的符号矩阵有关。对于n自由度结构，符号矩阵的个数为2n，因此，需要计算对应的2n个特征值和特征向量。当符号矩阵确定时，利用每个符号矩阵对应的特征向量，可对式(11)进行解耦计算，进而实现改进迟滞阻尼模型的模态叠加法。

利用特征向量和加速度反应谱，可计算每个符号矩阵对应下的地震作用效应，但为了保证结构设计的安全性，用于设计的地震作用效应须选择最不利情况，即多种地震作用效应中的最大值，从而可实现改进迟滞阻尼模型的抗震分析SRRS法。

2 基于改进迟滞阻尼模型的加速度反应谱

采用改进迟滞阻尼模型时，单自由度体系的时域积分计算仍按照时间步长Δt进行离散，任意时刻可表示为tk=kΔt(k=0,1,2…)。当Δt取值足够小时，可利用tk时刻结构的动力响应确定tk+1时刻的符号矩阵，并得到tk+1时刻的运动方程，由此进行时域迭代计算。利用单自由度的加速度响应，可得到基于改进迟滞阻尼模型的加速度反应谱。

加速度反应谱是结构抗震分析SRSS法的重要依据。以两条地震波为例，分析了改进迟滞阻尼模型加速度反应谱和粘性阻尼模型反应谱之间的差异。

在图2和图3中，计算所得的两条地震波作用下改进迟滞阻尼模型(CZ)的加速度谱值和粘性阻尼模型(NZ)的加速度谱值表明：在短周期段，CZ计算的加速度谱值小于NZ计算结果；在中周期段和长周期段，CZ计算的加速度谱值大于NZ计算结果。

图2 迁安波东西分量加速度反应谱Fig.2 The acceleration response spectrum of east-west Qian-an wave

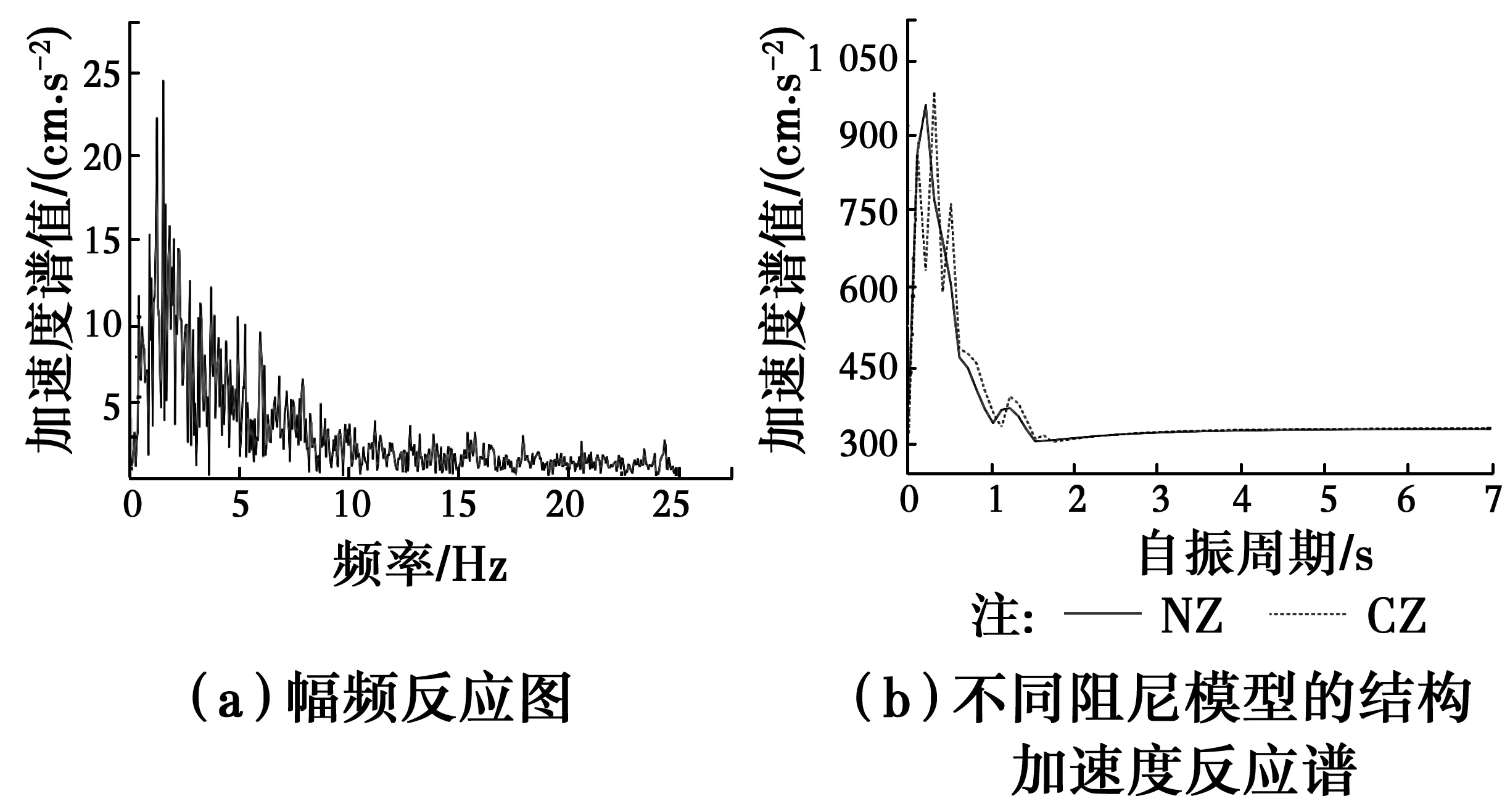
图3 El Centro波南北分量加速度反应谱Fig.3 The acceleration response spectrum of south-north El Centro

由于本文的重点在于研究迟滞阻尼理论的改进以及混合结构SRSS法的实现方法，对于迟滞阻尼理论反应谱的深入分析以及两种阻尼模型对应的设计反应谱的差异和对地震响应计算结果的影响，有待后续研究进一步澄清。与此同时，考虑到基于粘性阻尼理论的规范设计反应谱存在人为抬高拉平的做法[18]，故在后续算例中采用改进迟滞阻尼模型进行SRSS计算时，仍暂时借用规范的设计反应谱。

3 算例分析

如图4所示，以不同材料组成的3层剪切型框架结构为例，其具体参数为：抗震设防烈度为8度，设计基本地震加速度为0.20g，设计地震分组为第2组，场地类别为II类，钢结构的阻尼比为0.02，钢筋混凝土结构的阻尼比为0.05。

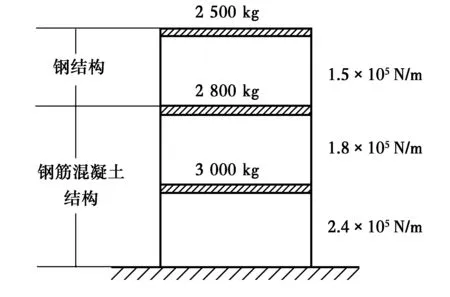
图4 竖向混合结构框架的质量和刚度分布图Fig.4 The mass and stiffness distribution of vertical mixed structure

质量矩阵为

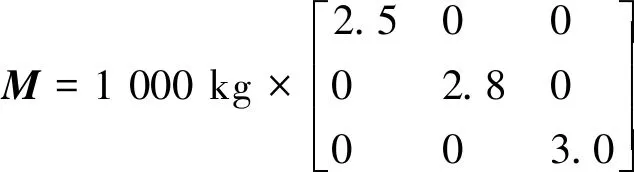
(16)

刚度矩阵为

(17)

阻尼矩阵为

(18)

对于3层框架，其符号矩阵共有8个，因此，需要计算每个符号矩阵对应运动方程下的框架层间剪力。如上文所述，基于改进迟滞阻尼模型的SRSS法可暂时采用规范反应谱，据此可计算出8个符号矩阵对应下的层间剪力，其结果如表1和图5所示。

在图5中，绘制了层间剪力的散点图，可得到最大剪力包络线，即选择最不利地震作用效应组合，从而计算出改进迟滞阻尼模型下的框架层间剪力。

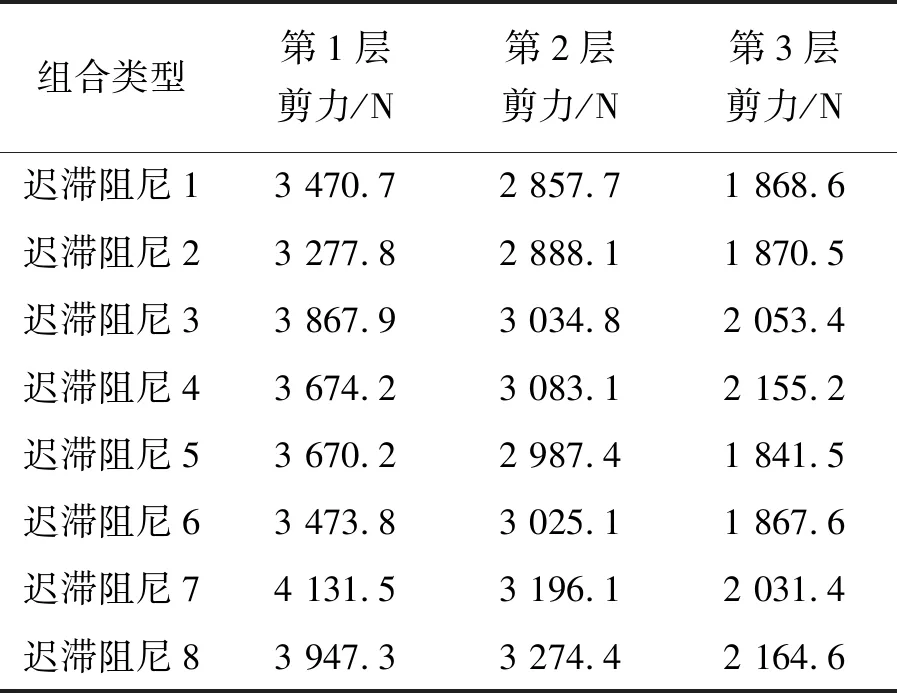
表1 采用改进迟滞阻尼模型计算的层间剪力Table 1 Calculated story shear forces by improved hysteretic damping model

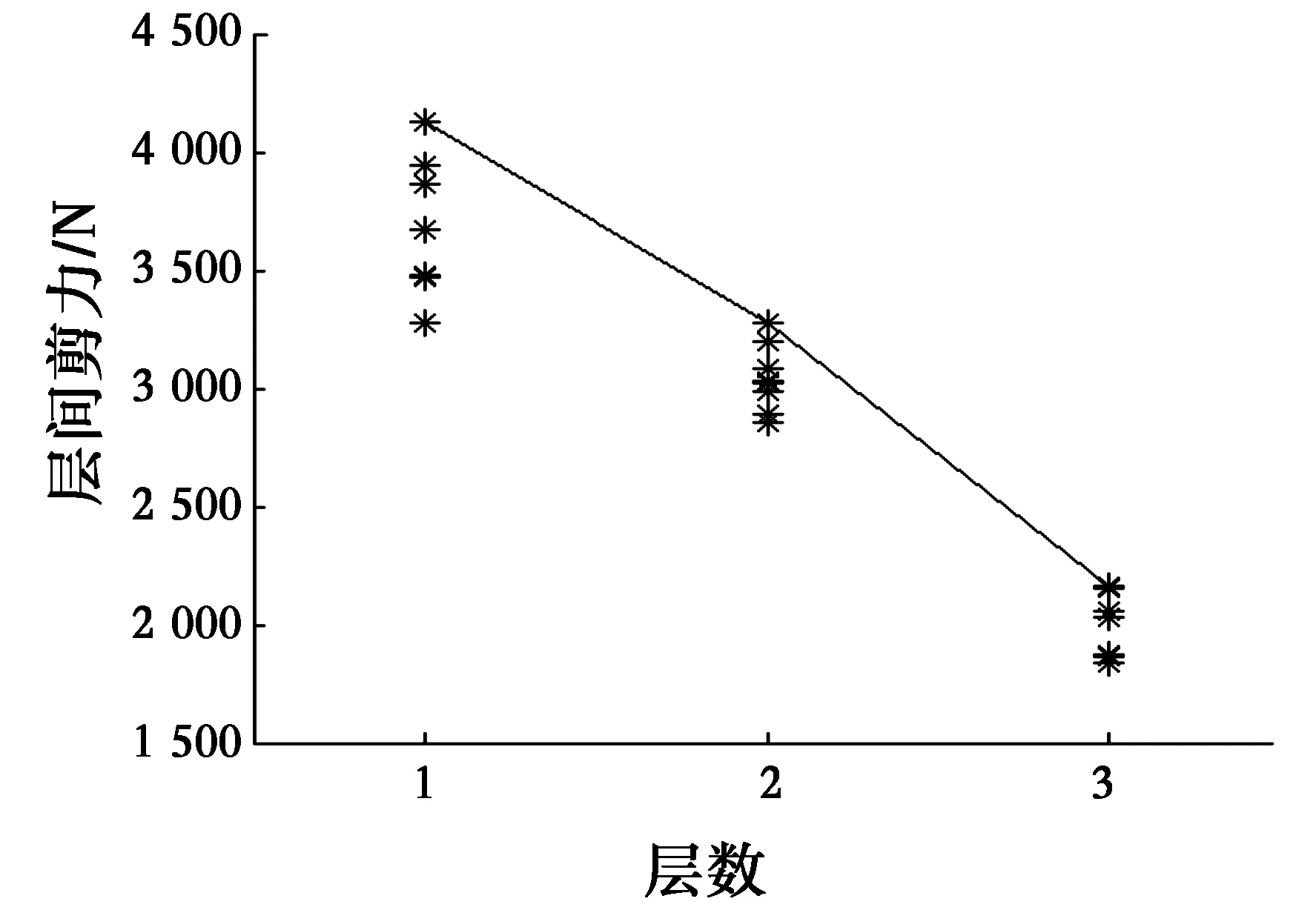
图5 基于改进迟滞阻尼模型的层间剪力Fig.5 Story shear forces based on improved

混合结构基于粘性阻尼模型的SRSS法可采用等效阻尼比ξd计算层间剪力。选择等效阻尼比时，若直接取阻尼比的平均值，可得等效阻尼比为0.035；若采用复频率法[6]确定混合结构振型阻尼比，将质量参与系数作为权系数进行加权平均，得到的混合结构等效阻尼比为0.038 9。分别采用粘性阻尼模型的SRSS法(NZ_SRSS)和改进迟滞阻尼模型的SRSS法(CZ_SRSS)计算框架的层间剪力，其结果见表2。

表2 不同方法计算的层间剪力Table 2 Story shear forces with different methods

CZ_SRSS的计算结果较NZ_SRSS(ξd=0.035)计算的层间剪力增加幅度为14.81%～16.75%，表明CZ_SRSS的计算结果普遍较大，且顶层剪力增幅最大，达到16.75%；CZ_SRSS的计算结果较NZ_SRSS(ξd=0.038 9)计算的层间剪力增加幅度为16.92%～19.14%，其增幅规律类似，且顶层剪力增幅达到19.14%。

对于N层剪切型框架，第k层结构在符号矩阵中对应的对角元素为1，其他层结构对应的对角元素为-1，即

(19)

此时，相比粘性阻尼模型下原结构的刚度分布情况，第k层结构对应的刚度增大，其他层对应的刚度减小，进而导致计算结果中第k层结构对应的地震作用效应增大。

基于改进迟滞阻尼模型的SRSS法选择每个符号矩阵对应下的最大地震作用效应，进而形成最不利地震作用效应组合，使得改进迟滞阻尼模型计算的地震作用效应大于粘性阻尼模型。

4 结论

经理论推导和算例分析，得以下结论：

1)改进迟滞阻尼模型具有每周期耗散能量与外激励频率无关的优点，但改进迟滞阻尼系统不再保持线性特征，具有局部的非线性特征。

2)与粘性阻尼模型相比，基于改进迟滞阻尼模型的模态叠加法可适用于非比例阻尼矩阵的混合结构。

3)基于改进迟滞阻尼模型的混合结构抗震分析SRSS法需要计算每种符号矩阵下的地震作用效应，计算量相对较大；若选择最不利地震作用效应组合，改进迟滞阻尼模型计算的地震作用效应比粘性阻尼模型计算的地震作用效应更大，其增大幅度约为15%～20%。