风驱雨作用下桥梁主梁颤振节段模型试验研究

雷旭,陈政清,华旭刚,牛华伟,韩艳

(1.广东电网有限责任公司 电力科学研究院，广州 510080；2.湖南大学 风工程试验研究中心，长沙 410082； 3.长沙理工大学 土木工程学院，长沙 410114)

随着新材料、新工艺的涌现和结构计算理论的不断完善，未来桥梁将会朝着超大跨方向发展，如刚建成不久的杭州湾和港珠澳跨海工程,就包含一批超大跨度桥梁。这类结构柔度较大，以致其风振效应可能成为影响结构安全的关键因素。目前，纯风作用下的桥梁振动特性研究已经非常成熟[1]，而实际工程中，特别是沿海和峡谷地区，大风一般伴随降雨，风雨耦合对结构产生作用，若要精确考虑这类动力敏感结构的风振响应，以确保其抗风稳定性，对降雨影响做仔细研究十分必要。

风驱雨对结构影响的研究虽早有开展，但主要集中于建筑结构和航空航天[2-4]以及拉索风雨振[1，5]研究领域，较少涉及其对主梁这一桥梁主要构件的影响，由于主梁构造和受力的特殊性，使得风驱雨对其气动特性的影响需专门研究，特别对于大跨桥梁中跨高比较大的柔性主梁，更具有必要性。近年来，已有一些学者开展此类工作，顾明等[6]模拟了风驱雨作用于薄平板的试验，依据试验结果，其初步认为，降雨对阻尼项气动导数有较明显的影响。辛大波等[7-8]进行了风驱雨对主梁的试验和数值分析，结果表明：与扭转气动阻尼密切相关的颤振导数受降雨影响明显，随雨强增大，临界风速先增大，后减小，但即使空气含水量达到65 g/m3， 临界风速仅提高约6.8%。胡俊[9]将风驱雨作用以力和阻尼形式代入有限元进行分析，结果表明：200 mm/h的雨强下，临界风速仅增大5.86%，但其对抖振影响比较显著。赵林等[10]依据风驱雨主梁模型试验，认为雨滴冲击力对定常气动力的影响相比积水而言可以忽略。钝体断面气动性能受降雨的影响比流线断面更加明显，其会改变频率、阻尼与气动导数，并在一定程度上降低颤振临界风速。以上研究表明：风驱雨试验是此类研究的重要手段，相比数值模拟，其更接近实际，但目前最大的问题是，对于雨荷载的相似关系没有得到解决，使得上述各结论的正确性难以相互比较验证和换算至原型以指导实际。针对这一问题，虽然已有学者对其进行研究，如Bilanin[11]和Cao等[4]假设雨滴大小和间隙可调，并依据含水量不变的原则，利用量纲分析法得到了理论的雨强相似关系，但现有的降雨设备难以达到其要求。Surry等[12]和唐顺勇等[13]人依据弗劳德数一致得到了风驱雨作用于建筑迎风面时的雨滴密度相似比为1:1，但对于竖向受载不可忽略的主梁断面，此相似关系显然不能适用。针对以上研究的不足，本文首先推导了主梁风驱雨试验的雨强简化相似比，然后在试验室实施了风驱雨条件下对桥梁危害最大的主梁断面颤振试验，获得颤振导数与临界风速随雨强的变化规律，依据雨强相似比对试验结果进行了分析，为大跨桥梁抗风研究的精细化提供了一定的参考。

1 降雨对结构风致作用的影响

1.1 自然降雨特性

自然雨滴形态一般被近似认为是球形，且雨滴谱满足M-P分布[14]，根据这一模型，空气中直径为D的雨滴数密度可表示为

N(D)=N0e-λD

(1)

式中：N0(8 000 m-3/mm)为雨滴数密度参量；=4.1I-0.21，是与雨强I(mm/h)直接相关的尺度参量。

空气含水量WL(g/m3)可根据式(1)的雨滴数密度计算如下

(2)

式中：D为雨滴直径，设雨滴直径范围为0～∞之间;r为水的密度,g/m3。

D粒径雨滴的竖直终点落速和水平速度可以表示为[15]

vr(D)=9.58(1-exp(-(D/1.77)1.147))

(3)

ur(D)=кU

(4)

式中：ur(D)与vr(D)分别为雨滴水平和竖向冲击速度；к是雨滴水平冲击速度修正常数[16]；U是水平风速值。

降雨相比无雨时对结构作用的变化体现在空气密度改变、雨滴对结构的冲击以及结构表面的积水3个方面。通过计算和相关文献提供的结果[17]可知：即使雨强为1 000 mm/h，空气密度增大量仅为2%，完全可以忽略，后续仅需分析降雨冲击及其引起的表面积水的影响。

1.2 降雨冲击力

以标准矩形断面图1(a)为例，风驱雨的作用形式如图1(b)所示。I区和II区分别为主梁上表面和迎风侧面。将不同大小的粒径用等效直径D0表示，并假设单位体积内直径D0的雨滴数为n0；ur0为风速也即雨滴水平速度，vr0为雨滴竖直向落速。

图1 主梁断面受风驱雨作用示意图Fig.1 Schematic diagram of the effect of raindrops impacting on the

N=(LHur0+LBvr0)τn0

(5)

式中：矩形的长、宽、高用L、B、H表示。

雨滴竖向动量Prv表示为

(6)

上式将水平速度ur0替代vr0即可得水平动量Pru。根据动量定理可得

(7)

式中：Frv为雨滴竖向平均冲击力，等式两边消除同类项后可得Frv的表达式，即

Frv=(LHur0+LBvr0)WLvr0

(8)

若计算水平平均冲击力Fru，只需将括号外的vr0对应以水平速度ur0替代便可。

1.3 结构受雨积水

实际结构在降雨条件下的表面积水状态十分复杂，若对不考虑附属设施阻水作用的平顺主梁断面而言，其沿桥宽方向可合理的简化成单向自由排水坡面，如图2(a)所示。因水的表面张力有限，积水厚度存在极限，如图2(b)所示。

季天剑等[20]通过实验和回归分析得到了单宽一维自由排水路面积水厚度经验公式(9)，其与实验和实测吻合较好。

Hr=0.125 8I0.778 6S-0.314 7L0.671 5TD0.726 1

(9)

式中：Hr为水膜深度,mm；I为雨强，mm/min;S为坡度；L坡长，m；TD为路面构造深度，mm，一般道路路面TD值取0.1。

当雨强为1 000 mm/h，坡度2%的50 m坡长主梁积水按照式(9)计算为10 mm，主梁高度一般为3～4 m， 积水仅为主梁高度的0.33%，因此，除非桥面雍水严重，一般可不考虑积水对外形的影响。

图2 路面水流示意Fig.2 Schematic diagram of pavement water

2 雨荷载相似关系的确定

两系统完全相似是指各自对应的任意一对无量纲量的值必须相同，其表达式为

(10)

式中：f1/F1和f2/F2为无量纲值，1,2则分别代表第1和第2系统，无纲量为两系统各自物理量与对应特征值之比。

对于复杂的物理现象，因相似准则可能彼此矛盾，难以实现完全相似，可以根据研究目的选取主要准则，实现部分相似。

2.1 雨滴冲击雨强相似关系

由式(8)可知，竖向和水平雨滴冲击力的表达式为[18，21]

(11)

式中：ur、vr分别为雨滴的水平和竖向撞速；D、n分别为雨滴直径及其数量密度。

考虑顺风向的风荷载和雨冲击力比值模型和原型一致，可建立相似关系

(12)

式中：()m、()p分别表示模型和原型参数；CD为主梁的断面风致阻力系数，对特定断面形式其为常数；ρw为空气密度。

式(12)经化简后便是风驱雨条件下的顺风向冲击作用各参数缩尺比关系式，即

(13)

式中：λ()为模型对原型的缩尺比表示。

同样，可推得仅考虑竖直向冲击作用的各参数相似关系为

(14)

联合式(13)和式(14)，根据几何缩尺比一致(λB=λH=λL)可得同时满足顺风向和竖直向相似关系的降雨参数缩尺比为

(15)

式(14)、式(15)分别保证了冲击方向和空气含水量的一致性。此缩尺比未涉及Froude数，可避免某些风速比下其不能满足的问题。

目前的试验设备还难以满足式(15)中的λU=λvr这一缩尺条件，但可较精确模拟自然降雨的下落速度和雨滴形态，即λD=1、λvr=1，据此条件，并结合大跨度桥梁主梁宽高比大以及其竖弯振动为主的特点，就此假定侧向迎风面高度H=0，仅计算降雨对梁顶面的竖向冲击力。经过上述一系列的合理假设后，可计算得到桥梁主梁在风驱雨作用时的降雨参数简化相似关系为

(16)

根据雨强I与WL的关系式(2)，可得

(17)

式中：i为雨滴直径，其在1～j内范围变化，常数a=0.089、b=0.846。

最后，可得到适用于主梁断面的简化的模型和原型雨强相似关系为

(18)

2.2 表面积水雨强相似关系

因降雨而产生的表面积水层会给结构物附加一定的升力和扭矩，特别对于以竖向和扭转振动为主的主梁，当积水很深时，其对应的雨强相似关系也需加以考虑。

2.2.1 考虑结构风致和雨致三分力之比不变的雨强相似关系 根据相似原则，可建立考虑表面积水的风轴坐标下影响主梁竖弯振动的气动升力和扭矩相似关系表达式[18，21]

(19)

式中：FL、M为风致静气动升力和扭矩；FrL、M为降雨引起的相应值，因扭矩是由升力计算，故式(19)可只计算第1分式，其表示为

(20)

式(20)经过变换后得到

(21)

将经验公式(9)代入式(21)，可得对应的雨强相似关系表示为

(22)

式中：λI、λL、λTD、λU分别为雨强、坡长、路面构造深度与风速的缩尺比。

2.2.2 考虑结构质量(尺寸)与积水质量(尺寸)之比不变的雨强相似关系 由结构和积水质量比值一致的相似原则，可得对应缩尺关系为

(23)

式中：ρs为质量密度，对于风洞实验，λρs=1。

由积水厚度计算公式(9)，式(23)的相似关系可以变换为

(24)

基于尺寸比值一致时，相似比同为式(24)。

2.3 试验雨强相似关系选取

若同时考虑雨滴冲击和表面积水雨强缩尺比，其会相互矛盾。计算和试验观察均表明，积水厚度和质量相比主梁可忽略，因此，对于本文的颤振响应试验，可以只考虑由降雨冲击推导的雨强相似关系式(18)。

3 风雨耦合作用下颤振节段模型试验

3.1 试验背景和工况

分别选取无原型对应的标准矩形断面(用于对比分析)、湖南洞庭湖大桥的π型断面(主跨径880 m、梁高3 m、宽高比10.3)和海南洋浦跨海大桥的流线型边主梁断面(主跨径820 m、梁高3 m、宽高比12.0)进行风驱雨试验，在湖南大学HD-2开口风洞中进行，试验环境见图3。降雨由QYJY-501型人工模拟降雨器实现，此装置喷出雨滴的物理形态和竖向下落速度和自然界十分接近，且覆盖范围的均匀度良好。

图3 风驱雨试验平台Fig.3 Test platform for wind driving

模型的安装布置如图4(a)所示，为避免侧向振动，模型两侧拉有限位钢丝。缩尺后的模型尺寸如图5所示(单位：mm)，模型相对原型的各参数缩尺关系如表1所示。通过试验发现：不同攻角下的风驱雨试验规律基本相同，考虑篇幅限制，仅对0°风攻角的试验结果予以分析，并据此得到结构颤振响应随雨强大小的变化规律。

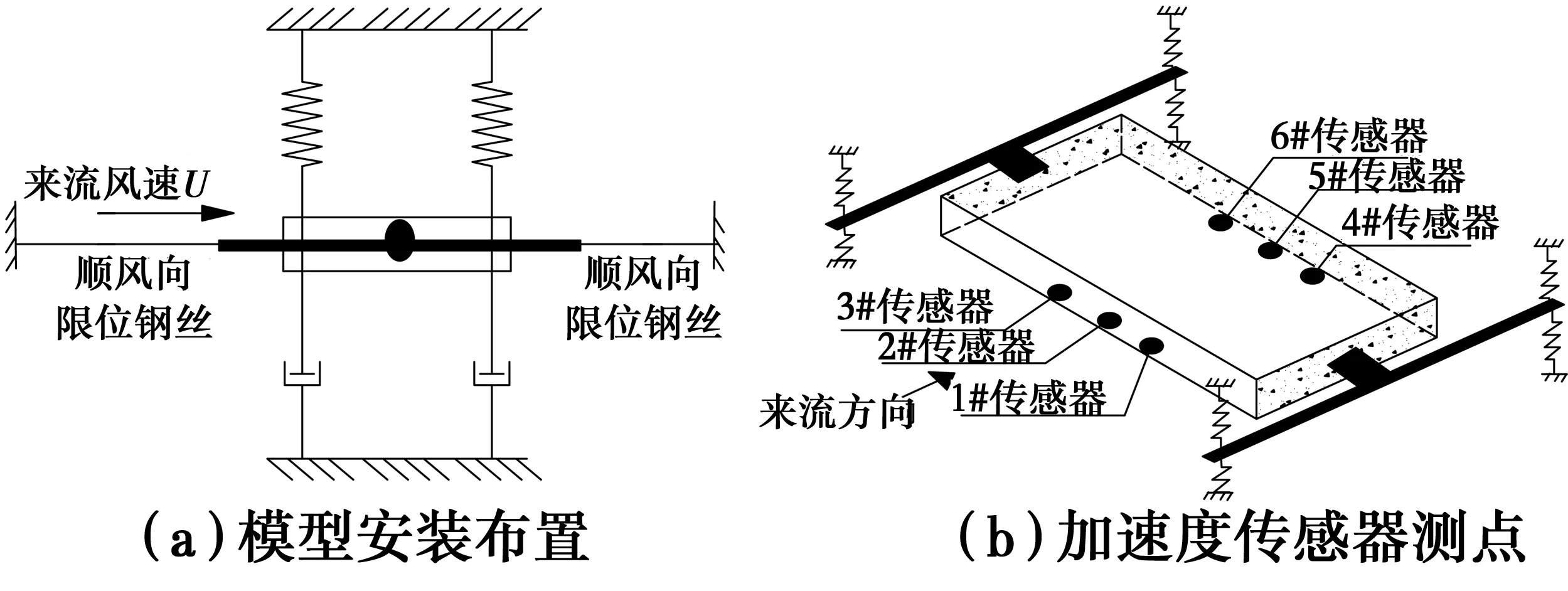
图4 颤振试验装置示意图Fig.4 Schematic diagram of flutter vibration test device

图5 三类模型主梁断面Fig.5 Three kinds of main grider

模型名称几何缩尺比风速缩尺比雨强缩尺比矩形主梁模型1∶11∶11∶1π型主梁模型1∶501∶24.511∶1 923流线型边主梁模型1∶601∶131∶430

3.2 降雨对结构的颤振导数的影响

风作用下的结构自激气动升力Lae以及扭矩Mae用式(25)表述为

(25)

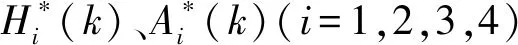
运用文献[22]中提出的分段扩阶最小二乘迭代法,通过弯扭自由振动获取了断面气动导数，0度试验攻角下的断面颤振导数测试结果如图6～图13所示。值得注意的是，表1所给出的雨强缩尺比是依据风、雨竖向冲击力比值一致所确定(公式(18))，而颤振导数对主梁气动外形、阻尼比等因素高度敏感，简单的使用表1相似关系做近似处理会造成很大误差，其不可用于气动导数试验，故量化的变化规律不能由此获得。

由图6～图13曲线的对比可知：风驱雨条件下的颤振导数相比无雨时会有些许变动，但基本没有改变其随折减风速的变化规律。不论是竖向、扭转还是交叉导数，其变化的量值基本相当，没有明显差异。另外，各导数随雨强的增大，其变化规律并不明显，这可能是由于各影响因素(雨滴冲击效应、表面积水带来的外形改变以及结构阻尼的变化等)之间的复杂耦合所致。随着约化风速的增大，不同雨强下的结果差异有所增大，表明高风速下风驱雨下的雨滴冲击力对结构气动特性影响增加。

图6 试验条件下的随雨强和折减风速的变化Fig.6 Change of flow with the non-dimensional wind speed and rainfall intensity in the test

图7 试验条件下的随雨强和折减风速的变化Fig.7 Change of flow with the non-dimensional wind speed and rainfall intensity in the

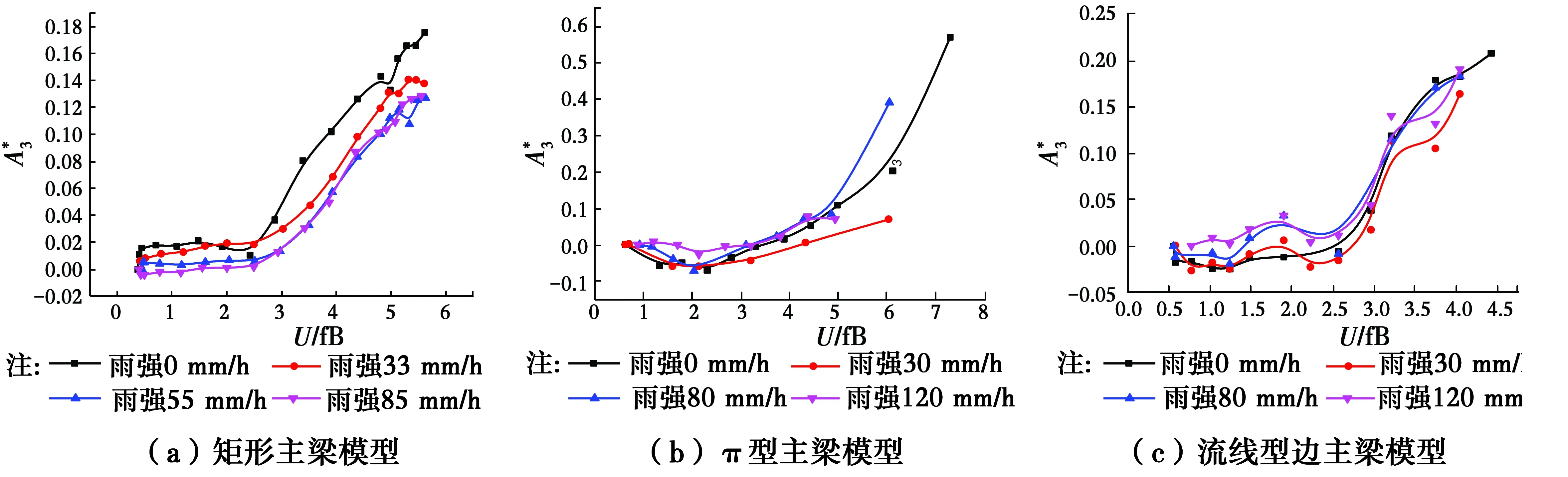
图8 试验条件下的随雨强和折减风速的变化Fig.8 Change of flow with the non-dimensional wind speed and rainfall intensity under in the test

图9 试验条件下的随雨强和折减风速的变化Fig.9 Change of flow with the non-dimensional wind speed and rainfall intensity in the test

图10 试验条件下的随雨强和折减风速的变化Fig.10 Change of flow with the non-dimensional wind speed and rainfall intensity in the test

图11 试验条件下的随雨强和折减风速的变化Fig.11 Change of flow with the non-dimensional wind speed and rainfall intensity in the test e

图12 试验条件下的随雨强和折减风速的变化Fig.12 Change of flow with the non-dimensional wind speed and rainfall intensity in the test

图13 试验条件下的随雨强和折减风速的变化Fig.13 Change of flow with the non-dimensional wind speed and rainfall intensity in the

3.3 风雨耦合作用时结构的颤振临界风速

通过节段模型风驱雨风洞试验模拟了各断面的颤振发生过程。图14和图15给出了0°攻角下的模型断面振动响应(竖弯和扭转)随雨强的变化规律。

图14 不同试验雨强下的模型竖向振动响应Fig.14 Vertical vibration response of the model flow with different rainfall intensities in the

图15 不同试验雨强下的模型扭转振动响应Fig.15 Torsional vibration response of the model flow with different rainfall intensities in the

由图14和图15中(矩形断面因其颤振形态为纯扭转，故图14(a)中的试验结果没有明显竖弯位移，表现为抖振，其结果不具备相应的规律性，不作为分析参考)不同雨强下断面竖弯和扭转位移随风速的变化可知：颤振的临界发散点随雨强增大有所延后，风速相同时，雨强越大，主梁振动幅度总体表现为减小趋势，说明降雨有利于减轻颤振响应和增大临界风速。以洞庭湖大桥的π型主梁和洋浦大桥的流线型边主梁断面扭转位移均方值试验结果为例(分别取0.5°和0.05°作为颤振发散点)，可知120 mm/h雨强下的发散点试验风速值要分别比无雨时高出28%和25%左右。为从理论上阐释降雨对结构的作用，以竖向振动为例，可知主梁在一个简谐周期内向下和向上运动时落入雨滴的相应动量方程为[18,21]

(26)

式中：Frv上和Frv下对应结构上下运动过程时的雨滴冲击力；mrs为时间内冲击主梁的雨滴总质量；vs、vr0则分别代表结构和雨滴移动的绝对速度。

主梁向上和向下振动时，雨滴冲击力分别作负功和正功，且正负作功时间均为半个周期，故一周期内冲击力所作的总功为

(27)

式中：T为一个周期内的结构振动位移总量。式(27)的计算结果表明，冲击力做的总功为负，其有利于减小振动，同样可推知，这一结论也适用于断面扭转运动和表面积水时的做功分析。上述试验结果若代入表1给出的本文雨强相似换算关系可知：两种主梁模型试验的雨强换算至实际后均超过104mm/h量级，这在自然界是不可企及的，因此，降雨对实际主梁颤振发生的影响可以忽略。

4 结论

依据自然界降雨特性，推导了适应主梁断面的试验雨强相似关系，通过风雨耦合试验平台实现了桥梁主梁断面不同雨强工况下颤振响应的对比测试，得到如下结论：

1)依据降雨冲击和表面积水特征，利用风雨作用三分力、质量以及外形等参数的无量纲特征值一致的原则，可以推导雨强缩尺比。由降雨积水厚度相比主梁高度可忽略、主梁颤振以竖向振动为主以及降雨装置的喷出雨滴接近自然界降雨特性的特点，可推知主梁颤振临界风速试验的简化雨强缩尺比等于风速缩尺比的2.364次方，对于颤振导数试验，因其影响因素复杂，无法给出准确的雨强相似关系。

2)主梁断面的颤振气动导数变化无明显规律，各导数的变化量值相当，随风速增加,降雨引起的导数变化有所加大，但基本没有改变其随风速变化的整体趋势。

3)主梁的颤振临界风速随雨强的增大会有所增大，表明降雨对颤振的发生具有一定的抑制作用，虽然试验给出的结果显示雨强达到120 mm/h时，模型主梁断面的颤振临界风速可提高20%～30%，但考虑雨强缩尺比后，实际雨强远超自然界雨强极值，故认为降雨对主梁断面颤振失稳特征的影响几乎可以忽略。