低周反复试验轴力加载装置的系统摩擦力

杨红，郭超，王志军,1b，罗航

(1.重庆大学 a.土木工程学院；b.山地城镇建设与新技术教育部重点实验室 重庆 400045； 2.中国人民解放军96518部队，河南 洛阳 471300)

采用截面纤维模型，基于力的非线性梁柱单元等细化数值模拟方法已经能较好地对钢筋混凝土柱在弹塑性阶段的加卸载刚度、滞回特征等进行有效预测。但陆新征等[1-3]、戎贤等[4]、Moharrami 等[5]在研究中发现，钢筋混凝土(RC)柱的模拟承载力不同程度地低于试验结果，且随着轴压力增大，两者的差异相应加大。分析结果表明[6-7]，这种系统性误差主要与摩擦阻力有关，在柱、剪力墙、梁柱组合体试件等的低周反复试验中，施加轴压力的竖向作动器主要通过钢铰或滚轴导轨与反力架相连，试验过程中，钢铰和滚轴随柱顶位移而滑动或滚动必然会引起相应的摩阻作用，因此，该摩阻力将导致由水平作动器的力传感器测量的水平力较柱承受的真实值偏大。

《建筑抗震试验方法规程》[8]并未充分考虑摩擦力影响，仅规定滑动导轨的摩擦系数不应大于0.01。李林安等[9]通过机械试验分析了钢铰、轴承的滑动、滚动摩擦的性能，分别得出了与建筑抗震试验方法规程不同的铰轴滑动摩擦系数解析式；《机械设计手册》[10]的摩擦系数取值也与《建筑抗震试验方法规程》不同；Tanaka 等[11]研究了往复滑动中初始接触面条件对钢轴承摩擦系数的影响；Hanrahan等[12]研究了滚动摩擦系统摩擦系数取值；吴家杰等[13]通过不同的竖向加载装置分析了摩擦力对 RC 桥墩抗震性能影响。为了消除(减小)摩擦力引起的误差，Lavorato等[14]、Chang等[15]采用了不设置滑动支座的竖向力加载装置进行抗震性能试验研究。

目前，学者们对低周反复试验中因轴力加载装置引起的摩擦阻力如何计算缺乏研究。以型钢柱为例，通过弹性阶段的低周反复试验和相应的有限元模拟，建立了一种确定轴力加载装置引起摩擦力的计算方法；通过对RC柱的水平力测量值进行摩擦修正，提高了试验结果的准确性。

1 摩擦力量化分析方法与试验设计

1.1 摩擦力定量计算方法

以图1(a)所示悬臂柱为例，施加轴压力的竖向作动器上端、下端均通过钢铰轴(圆柱形的钢轴承穿过钢铰上摆、下摆的铰孔，形成铰接连接，以下简称铰轴)与试验柱构件、反力系统相连，随着柱顶水平位移增大，铰轴转动将引起相应的摩擦阻力。

整个加载装置主要在图1(a)所示的4处位置产生摩擦阻力，分别是：竖向千斤顶与反力架连接的铰轴(编号1)；竖向千斤顶与构件连接的铰轴(编号2)；柱顶与钢铰连接面之间可能存在滑动，形成相应的滑动摩擦力(编号3)；水平千斤顶与构件连接的铰轴(编号4)。笔者将上述由于整个加载装置引起的摩擦阻力统称为系统摩擦力(简称摩擦力)。

在试验过程中，上述4处位置的摩擦力并不相同。即使对于编号1、编号2的单个铰轴而言，其摩擦状态也较为复杂。试验过程中，当竖向作动器随柱顶位移左右摆动时，钢轴承与钢铰上、下摆产生相对转动，同时钢轴承也在上摆、下摆的铰孔空隙处相对滑动(当钢轴承加工质量偏低、铰孔直径偏大时，这种滑动更明显)，从而形成滚动摩擦和滑动摩擦混合作用的状态。此外，钢轴承和上下摆铰孔的初始形状并非理想圆形，随着压应力加大，在轴承滚动时，轴承和铰孔的接触面形状将发生微小变化，接触面愈软、形状变化愈大，滚动摩擦力就愈大。综上所述，整个加载装置的系统摩擦力与钢轴承、钢铰孔接触面的光滑程度、制作工艺等有关；此外，试验时启动加载、采数停顿、峰值卸载等可能产生静摩擦作用，其与水平位移行进中的动摩擦交替作用，进一步增加了加载装置摩擦状态的复杂性。

在图1(a)所示的钢筋混凝土悬臂柱的低周反复试验中，直接测量的水平力-位移曲线的水平力比真实值偏大，有两方面的原因：一是竖向作动器随柱顶水平移动逐渐倾斜，在水平方向形成的分力(见图1(b))；二是轴力加载装置引起的摩擦力(见图1(c))。

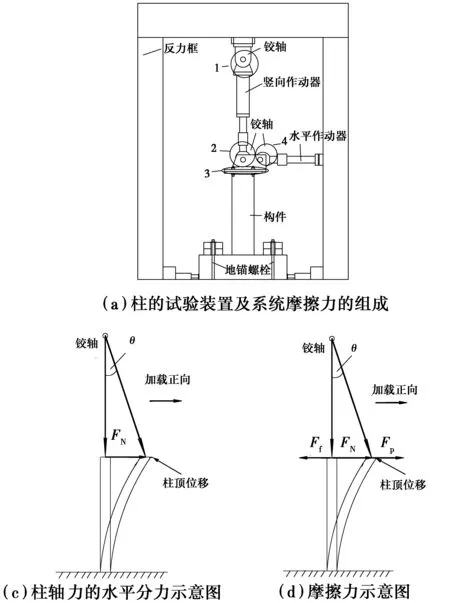
图1 轴力加载装置引起的摩擦力示意图Fig.1 Sketch of friction caused by axial

采用铰轴连接方式的试验中，随柱顶水平位移增加，竖向作用器与竖直方向形成的夹角(θ)会逐渐加大，故竖向作用器的轴向力除存在竖向分量(即柱承受的轴压力)外，还存在一个水平分量FN(见图1(b))，FN将使实际测量的水平力FP比柱实际承受的水平力更小。这种试验误差可以在试验完成后直接根据实测数据进行修正，其修正方法是：首先计算各柱顶位移下的θ(根据柱顶水平位移、竖向作用器上下铰轴的中心距实测结果进行计算)，然后计算轴压力N的分力FN，将其与水平作动器的实测结果FP叠加，结果即为考虑摩擦力修正之前的RC柱顶承受的水平力。

对于图1(a)所示的轴力加载装置(竖向作动器通过铰轴与试件、反力系统连接)，通过3个步骤定量计算该装置引起的摩擦力。

第1步，对型钢柱进行弹性阶段的低周反复试验，获得水平力-位移滞回曲线的测量结果。该实测水平力-位移曲线包含了摩擦力Ff、轴力水平分量FN的影响。理论上看，型钢柱弹性阶段的水平力-位移关系本是一条斜直线(若二阶效应的影响可近似忽略)，但由于摩擦力等影响，实测滞回曲线会形成滞回圈。

第2步，对于材料处于弹性状态的型钢柱，可通过有限元软件精确地计算各水平位移下的柱顶水平力(FM)。FM的计算结果不受摩擦力Ff、轴力水平分量干扰FN，为无摩擦的理想状态的结果。

第3步，将试验结果、有限元计算结果相结合，可按式(1)计算各位移状态下的摩擦力Ff。

Ff=FP+FN-FM

(1)

FN=N·θ

(2)

式中:Ff为施加轴力的竖向作动器等引起的系统摩擦力，FP为试验加载水平力(由与水平作动器相连的力传感器直接测得)，FN为竖向作动器轴向力的水平分量，FM为采用有限元模型计算的水平力，N为竖向作动器施加的轴向力(由与竖向作动器相连的力传感器测得)，θ为竖向作动器与竖直方向的夹角(见图1(b))。分析时，式(1)中各水平力均以图1(c)所示“加载正向”为正。

在第1步中，采用型钢柱试件进行低周反复试验的目的是消除材料非线性的影响，但不利之处是钢柱的二阶效应一般更为显著。因此，在第2步计算时重点考虑了二阶效应，建立能完善考虑二阶效应的有限元分析模型，并完成相应计算。

1.2 试验概况

2个钢柱试件编号为GZ-1、GZ-2，分别对应文献[16]中的RC柱SC-5和SC-6。应强调的是，4个试件采用了同一套加载系统(包括反力架、竖向作动器两端的连接铰轴、水平和竖向作动器等)，如图2所示。

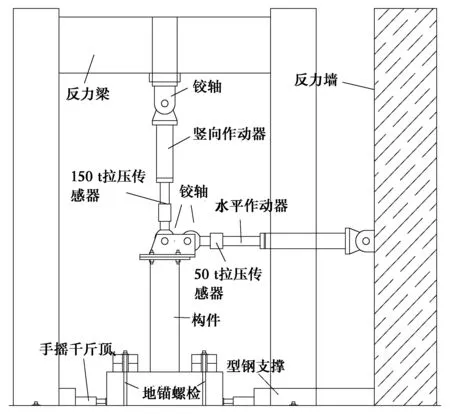
图2 试验加载装置图Fig.2 The loading system of

合理设计型钢试件，使其受力性能满足如下要求：型钢试件在整个实验过程中，始终在材料弹性阶段且其弹性阶段的最大顶点位移与相应RC柱破坏时的最大水平位移相近，此外，型钢试件目标位移下的水平承载力也接近相应RC柱的水平承载力。

试件所用钢材强度均为Q345B，试件尺寸见表1。

表1 钢柱试件尺寸与材料属性Table 1 Specimen size and behavior parameter of steel columns

按照《钢结构设计规范》[17]、《钢结构原理与设计》[18]，完成了试件腹板与翼缘连接焊缝、柱脚和柱顶连接铰以及其连接焊缝的设计、计算，结果如图3所示。测得的钢材基本力学性能见表2。

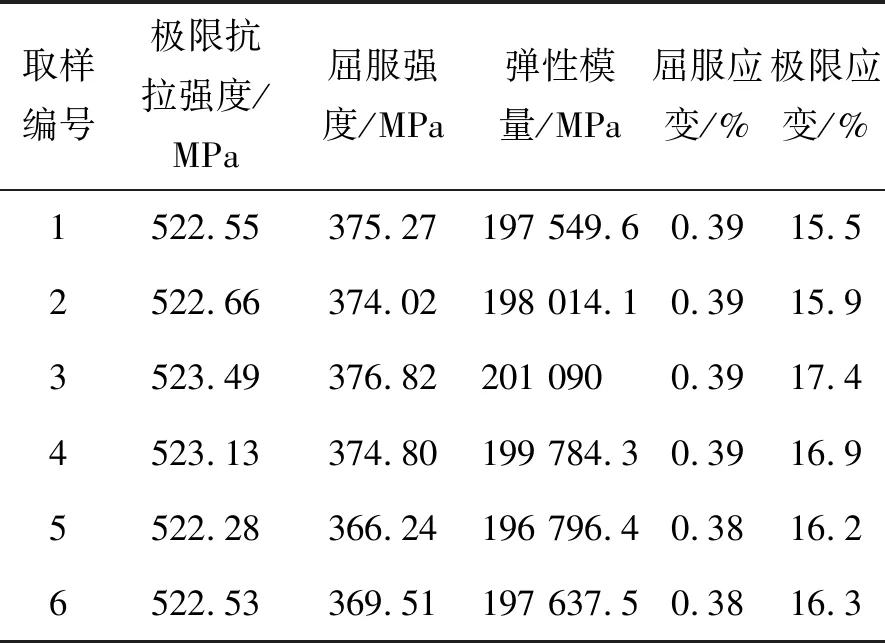
表2 钢材力学性能参数实测值Table 2 The measured performance parameters of steel

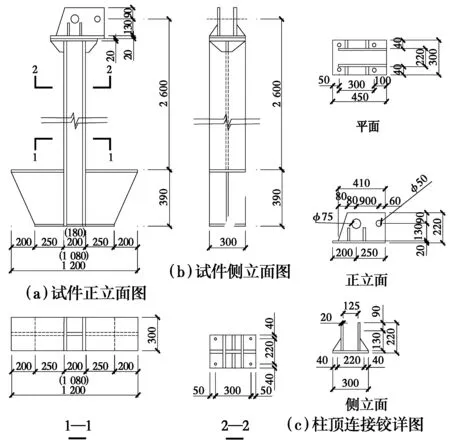
图3 试件尺寸和连接铰详图Fig.3 Detail drawing of specimen size and

采用拟静力方法对试件进行加载，加载装置如图2示。试验中，竖向轴力由150 t拉压作动器施加，水平作用力由50 t拉压作动器施加。水平荷载由水平作动器端部的50 t拉压传感器测量，试件柱顶位移由位移计测量。试验过程中通过采集的应变数据随时判断试件是否处于弹性状态。应变片共设4排，各排应变片距离柱底座上表面分别为50、150、250、350 mm。

试件GZ-1分别在轴力等于288、576、928 kN下各进行了3次弹性低周反复加载(共9次试验)，试件GZ-2分别在轴力等于122 、244、 365 、576 、928、1 293 kN下各进行了4次弹性低周反复加载(共24次试验)，每次试验结束后、开始下次试验前，均将铰轴与试件拆开并重新连接，使摩擦力归零。各试验均采用位移控制，其加载制度见图4，图中Δ为型钢柱柱顶位移，其各循环的位移幅值分别等于文献[16]中RC柱屈服位移Δcy(RC柱SC-5和SC-6屈服位移Δcy均近似取为7 mm)的1、2、3倍(即7、14、21 mm)。

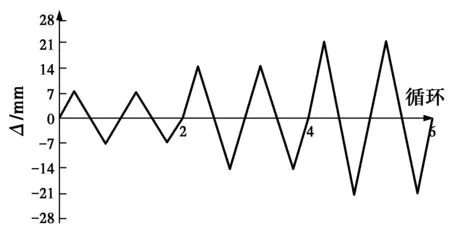
图4 水平荷载加载制度示意图

1.3 试验荷载-水平位移滞回曲线及修正

正式试验开始之前，对各试件进行了无轴力的验证试验。图5为试件GZ-1脱开柱顶竖向作动器、未施加轴力时的水平力(FP)-位移(Δ)曲线测量结果，可以发现，在无轴力状态下其试验结果仍然存滞回圈。

图5 试件GZ-1无轴力作用的原始试验结果与修正Fig.5 The revised test results and original test results of specimen GZ-1 without axial

由前文分析可知，柱顶施加轴力的铰轴脱开后，不会出现摩擦力Ff、轴力水平分量FN的干扰。经仔细分析发现，实测FP-Δ曲线形成滞回圈的原因是，试验过程中型钢柱试件顶部钢板相对于钢铰底板略有滑动(摩擦型高强螺栓直径较螺栓孔更小)。为了消除该因素影响，布置百分表测量该相对位移，并据其修正柱顶位移。如图6所示，百分表通过磁性基座固定在钢柱顶部，Δs为钢柱顶部相对于钢铰的相对位移(受拉为正)，Δt为位移计测得的柱顶位移值(受拉为正)，则真实的柱顶水平位移Δ=Δt-Δs。

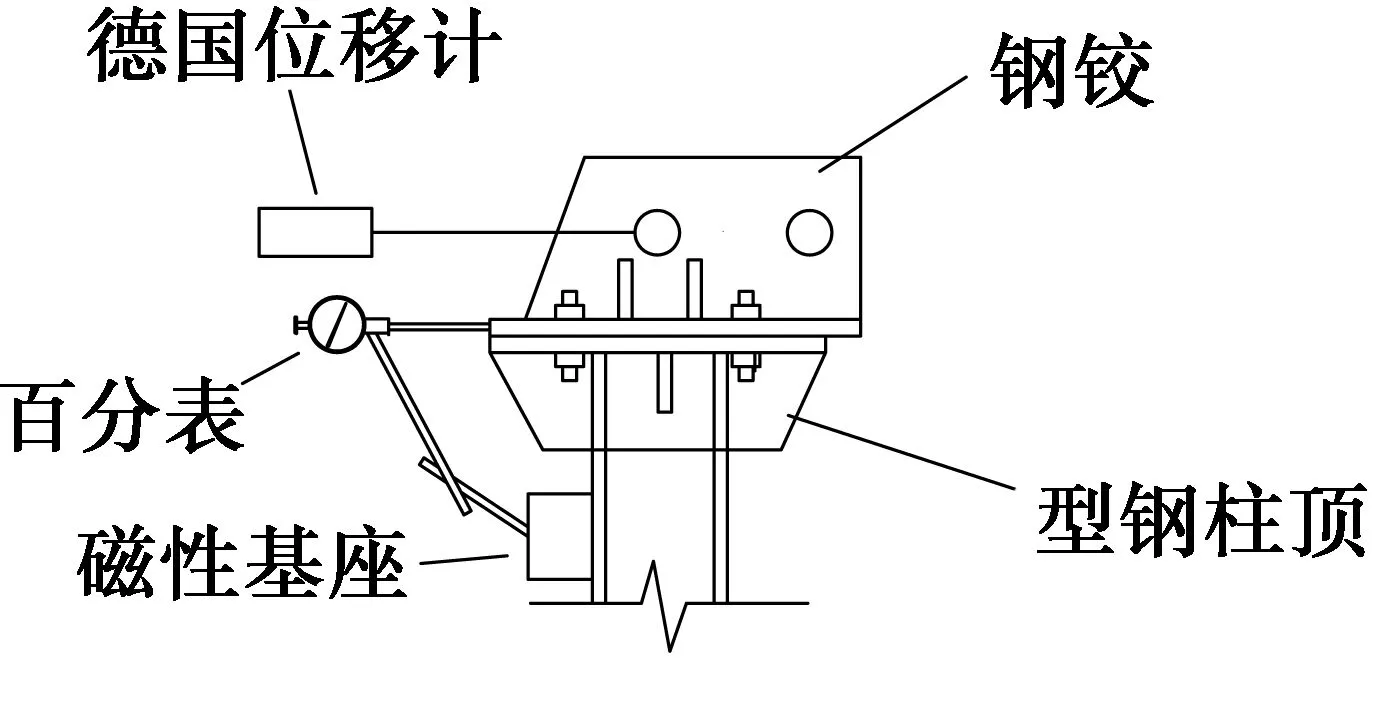
图6 柱顶相对滑移修正示意图Fig.6 The correction of column top’s relative

图5(b)表明，经修正后，无轴力下FP-Δ曲线不再出现滞回圈，表明其结果是合理的。

2 摩擦力计算结果与变化规律

2.1 有限元模拟与二阶效应

为了得到考虑二阶效应后试件的荷载-位移曲线计算结果，在OpenSees平台上，选取nonlinearBeamColumn单元建立型钢柱的有限元模型。由于nonlinearBeamColumn单元不能直接考虑P-δ效应，OpenSees也难以精确计算P-Δ效应，故采用舒启军[19]的研究成果进行计算。该方法根据Souza[20]的柔度法理论，通过在最终的刚度方程中直接按线弹性方式加入相应项，不考虑扭转变形与其余变形间的耦合作用，建立能够完全考虑二阶效应的柔度矩阵。

考虑P-Δ效应和P-δ效应的截面力表达式为[19]

S(x)=b(x)P

(3)

(4)

张勇[21]和舒启军[19]通过算例和试验验证了采用上述方法建立的有限元模型对计算二阶效应的准确性。计算时，钢柱截面采用纤维模型，将试件的左右翼缘各划分为5个纤维，腹板划分为4个纤维；钢材本构采用Steel02模型，影响过渡曲线形状的参数分别取20，0.925和0.15，应变硬化率0.01。

为了进一步验证上述有限元模型的正确性，以2个试件的无轴力试验结果为依据对其进行了校核。

无轴力作用下FP-Δ曲线试验结果(已对柱顶连接螺栓滑动进行了修正)和计算结果如图7所示，表明无轴力时两试件试验结果与模拟结果一致。

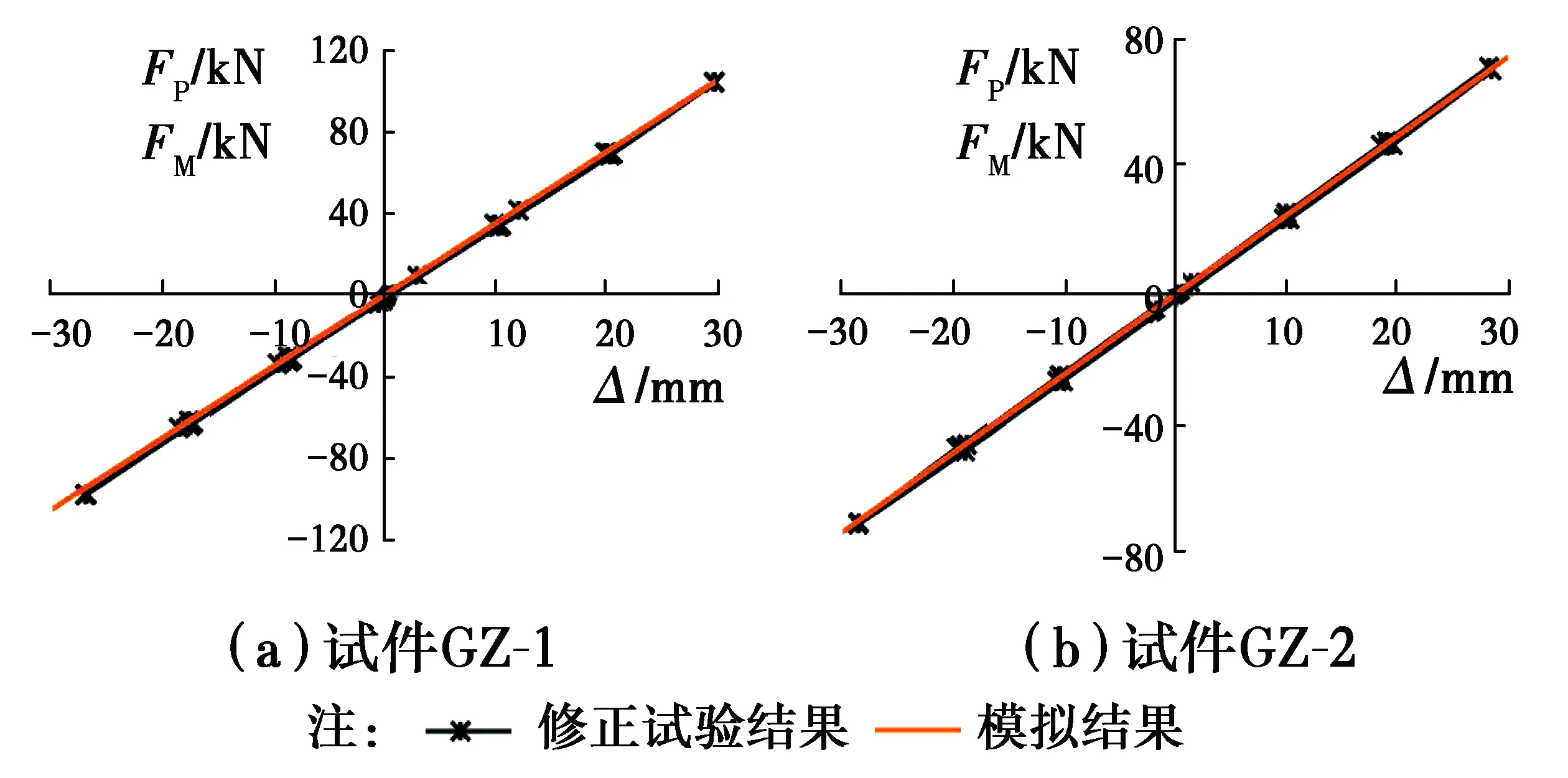
图7 无轴力作用时试件修正试验结果与计算结果对比Fig.7 Comparison of revised test and simulation result for specimens without axial

2.2 摩擦力变化规律与计算结果

2.2.1 荷载-水平位移关系试验和有限元计算结果

如前所述，试件GZ-1、GZ-2分别在不同轴压力取值作用下进行了数次独立的低周反复加载试验。图8和图9给出了多次试验中的一组典型试验结果(均已对柱顶连接螺栓滑动、FN进行了修正)，以及与相应有限元计算结果的对比。

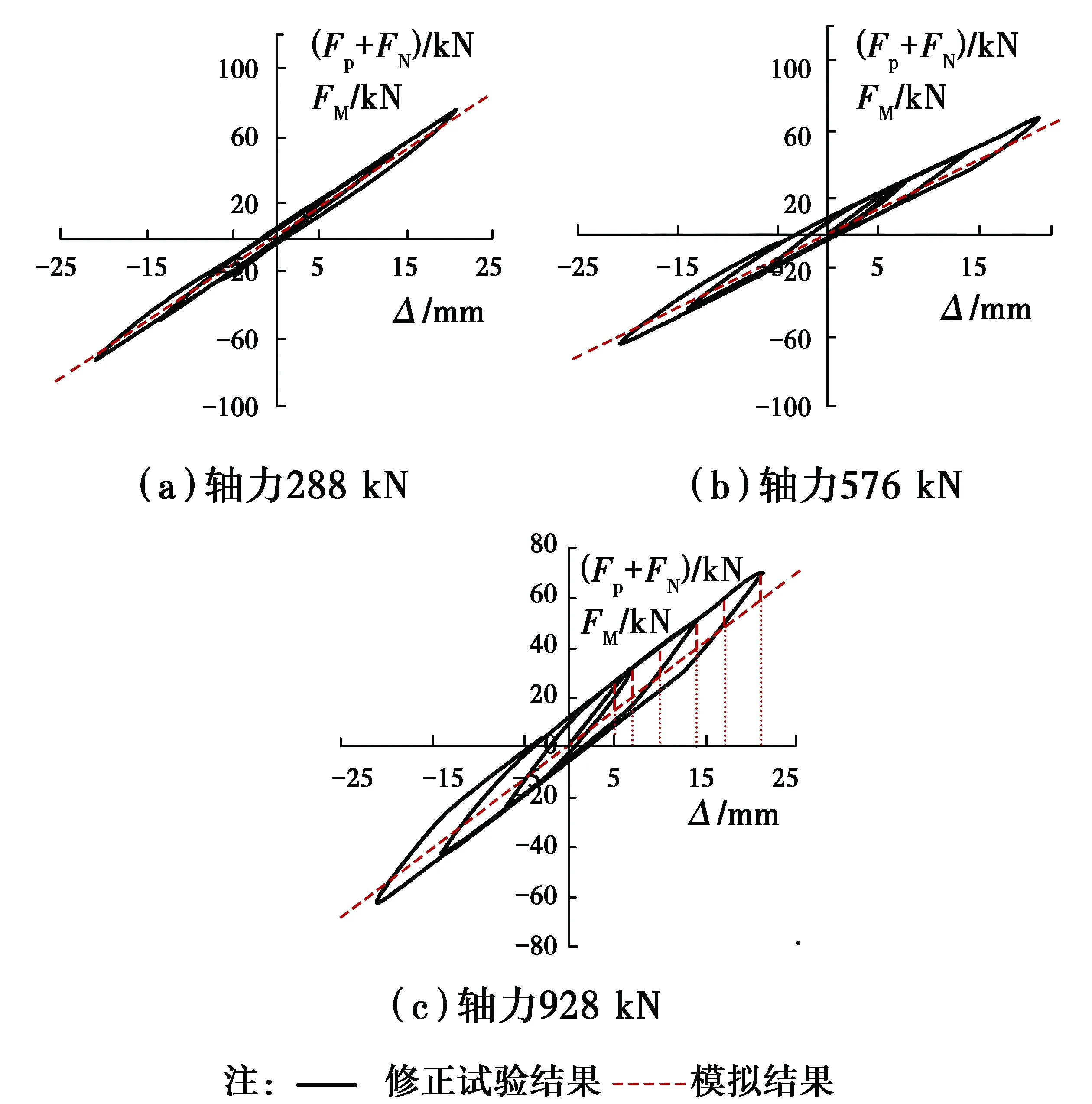
图8 试件GZ-1试验结果与模拟结果对比Fig.8 Comparison of test and simulation result for specimens GZ-1

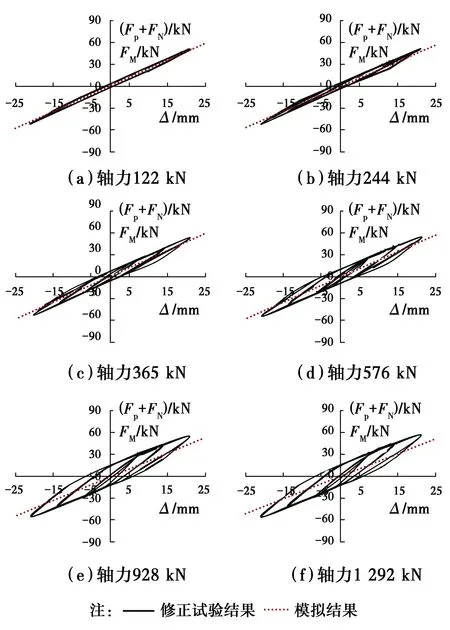
图9 试件GZ-2试验结果与模拟结果对比Fig.9 Comparison of test and simulation

在图8、图9中，有限元计算时试件处于无摩擦力的理想状态，且二阶效应影响很小，故型钢柱弹性阶段的FM-Δ曲线计算结果近似为一条斜直线。对于试验结果，虽然试件材料处于弹性状态，但受Ff的影响，且摩擦力在加载、卸载过程中大小和方向均有所改变(具体分析详后文)，故试件的水平力测量结果相应变化，并使柱顶水平力-水平位移形成了弹性滞回圈。

2.2.2 加载阶段的摩擦力 图8、图9表明，在加载过程中(除加载初始阶段外)，试验滞回曲线基本与无摩擦力的模拟曲线的斜率相同(平行)，即Ff在加载的大部分过程中基本保持不变，故近似选取±5、±7、±10、±14、±17、±21 mm等共6个位移点(其中，±7、±14、±21 mm为各循环的位移幅值)计算，并将其作为分析加载阶段的代表值。因此，根据不同轴力下多次试验的结果、有限元模拟结果，按照式(1)即可计算摩擦力。

以图8 (c)中GZ-1试件件在928 kN下第1次低周反复试验结果为例，说明正向加载阶段的摩擦力Ff计算方法。

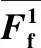
表3 轴力为928 kN时试件GZ-1的摩擦力计算结果Table 3 The calculated friction force at loading point of GZ-1 under 928 kN axial force kN

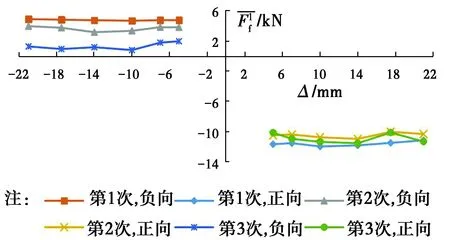
图10 轴力928 kN作用下试件GZ-1加载段 摩擦力平均值Fig.10 Average friction force of specimen GZ-1 under 928 kN axial force at loading

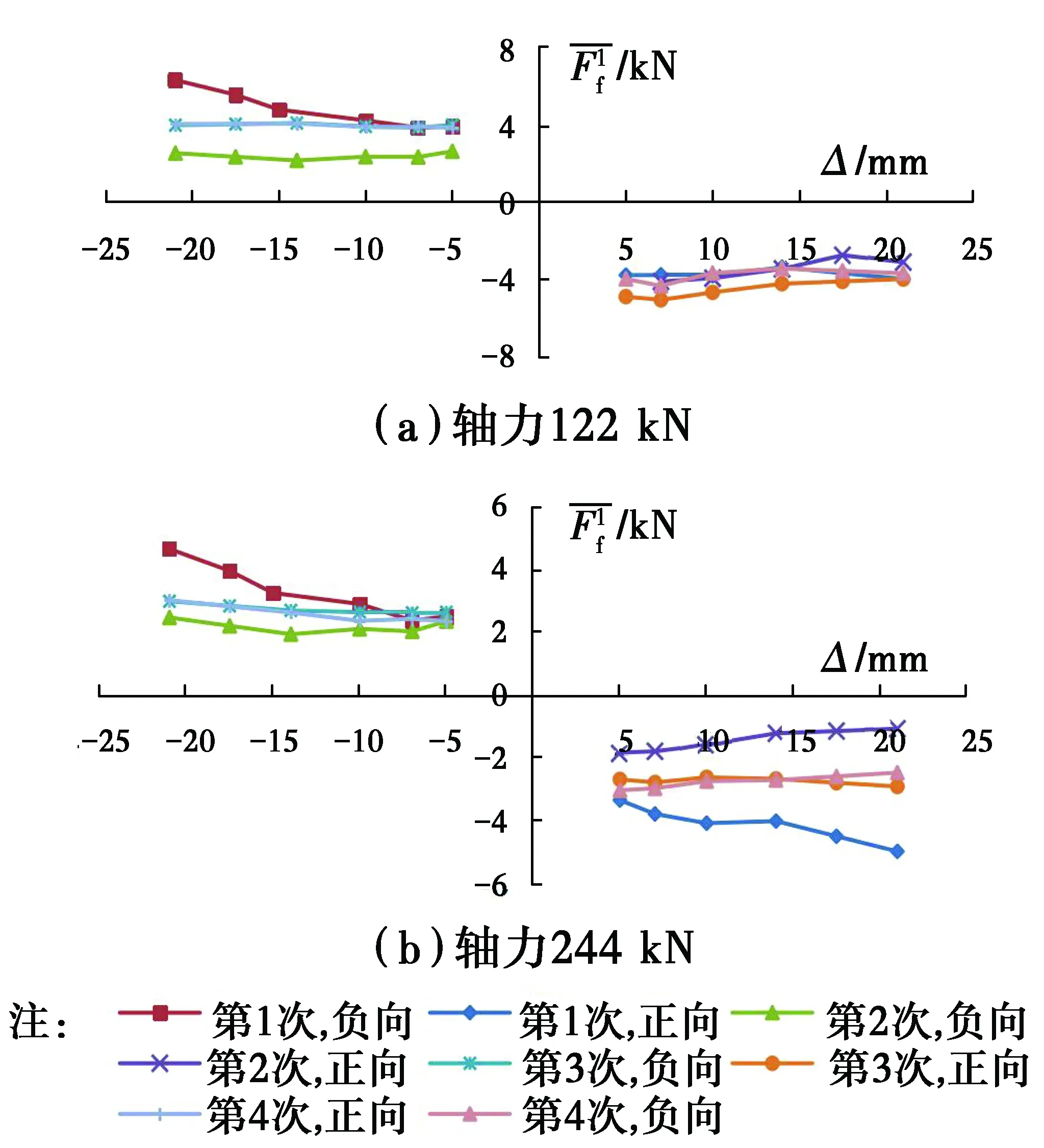
图11 试件GZ-2加载段摩擦力平均值 Fig.11 Average friction force of specimen GZ-2

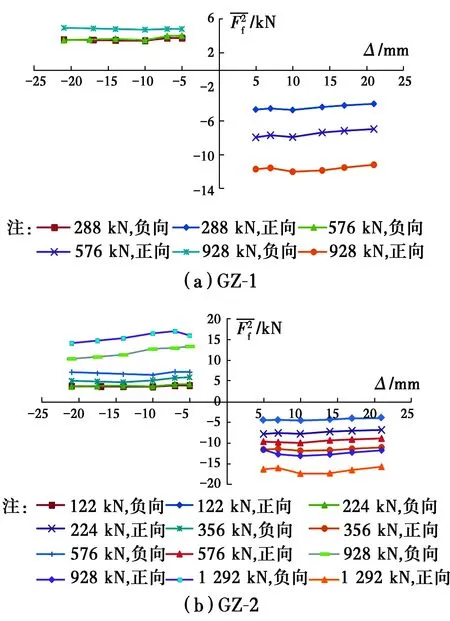
图12 各试件加载段摩擦力平均值Fig.12 Average friction force for specimens at loading

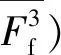
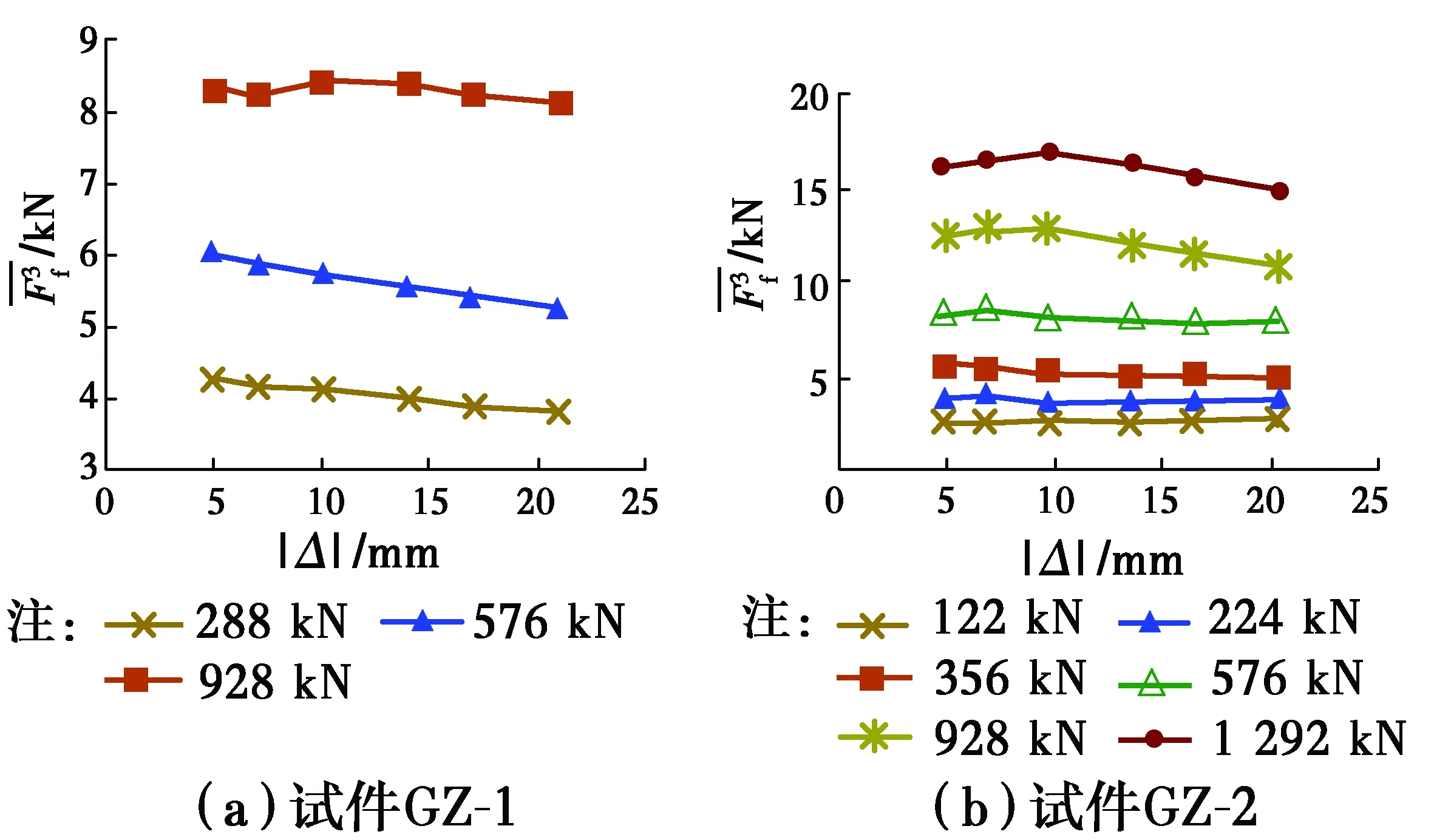
图13 各轴力作用下加载段摩擦力平均值Fig.13 Average friction force under different axial force at loading

2.2.3 卸载阶段的摩擦力 为分析卸载阶段摩擦力的变化规律，分别计算试件GZ-1、GZ-2 在轴力为928 kN下的卸载阶段摩擦力 (仅以柱顶位移幅值为±7、±14、±21 mm的3个循环的卸载段为例)，结果如图14所示。

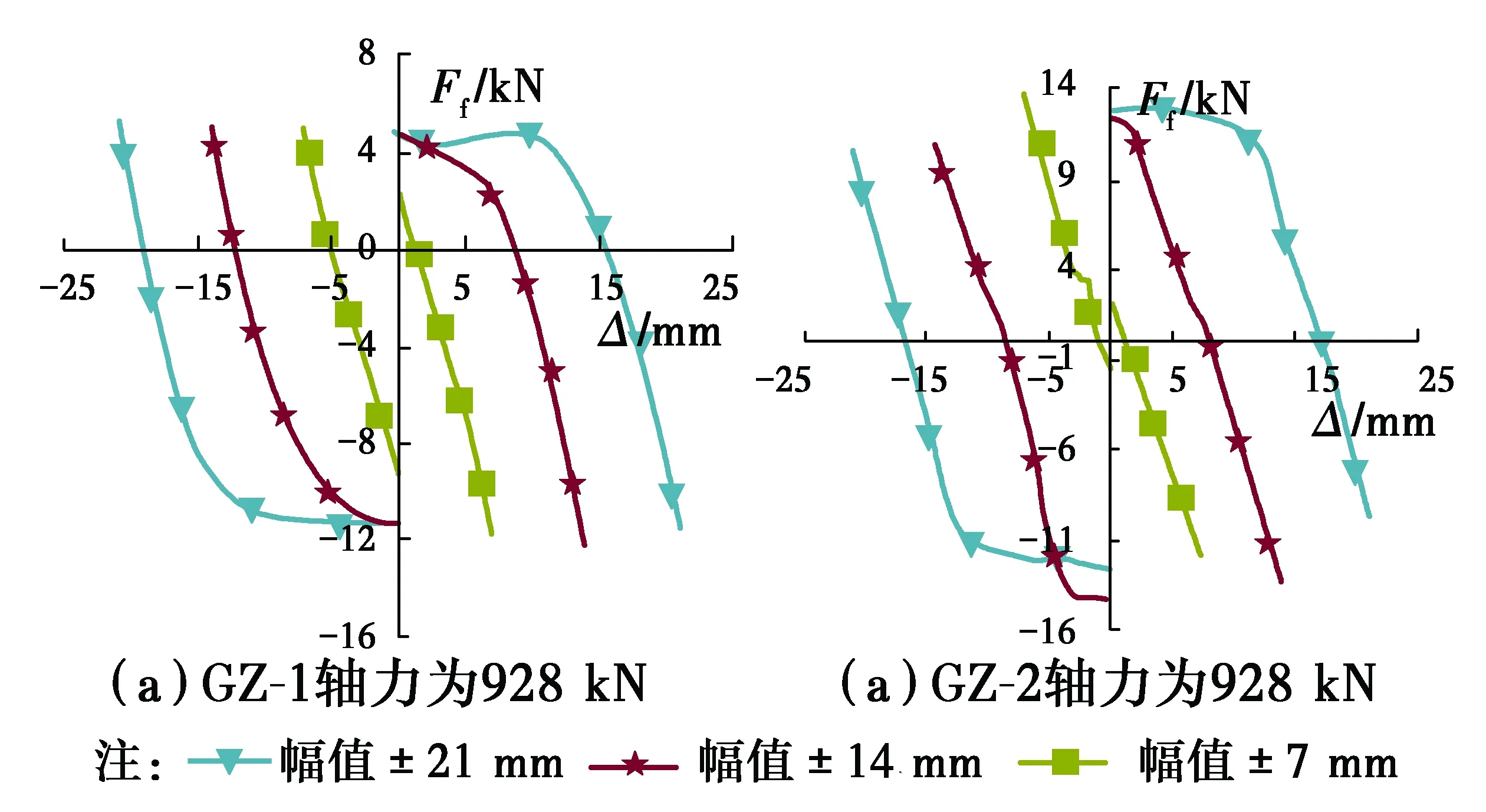
图14 试件卸载段摩擦力FfFig.14 Friction fore Ff of specimens at unloading

首先，以位移幅值为±21 mm的正向卸载阶段为例说明Ff的变化过程：在21 mm位移幅值时Ff为负值，在21～15 mm左右Ff会迅速变化为0，在15～10 mm继续迅速增加，然后，随着柱顶位移减小，趋于稳定(等于加载阶段的Ff)。

上述分析表明，在21 mm位移幅值处，试件处于加载、卸载的临界(转换)状态，加载阶段末Ff为负值，但开始卸载后，随着柱顶位移减小，Ff会经历一个“负向→绝对值下降→零→绝对值增加→正向”的变化过程，即摩擦力会改变方向，从而导致图14中蓝色曲线在21～10 mm经历了由负值变为正值的过程。

卸载阶段Ff改变方向的根本原因是，Ff的方向总是与运动方向相反。在加载过程中，Ff始终与运动方向相反，也就总是与作动器水平力FP方向相反，故卸载前的大小、指向基本不变。开始卸载的初期，FP方向不变(与加载时相同)，但很快柱顶位移运动方向变化，故Ff改变方向(数学符号变化)，并随后逐渐增大。

图14中只有幅值±21 mm的卸载段有较为明显的稳定段，幅值±7 mm、±14 mm的卸载段基本上只存在方向改变的过程。出现这种现象的原因是，在图8、图9的试验滞回曲线与模拟的FM-Δ线相交(Ff改变方向)的过程中，±7 mm、±14 mm循环测得的FP在卸载段的变化幅度一直有较大的增大或者减少(表现为卸载刚度变化)，模拟计算的FM基本线性变化，即其刚度基本不变，因此，按式(1)进行计算会导致Ff的正→负(或负→正)的变化过程较长，故幅值±7 mm、±14 mm的卸载段Ff的稳定段需柱顶水平位移进一步加大才能出现。

基于以上分析，结合图8、图9可知，卸载过程是形成弹性滞回圈的过程，因卸载过程中试验滞回曲线与有限元计算的FM-Δ线相交，故按式(1)计算的卸载摩擦力正、负号会变化，即摩擦力方向变化。

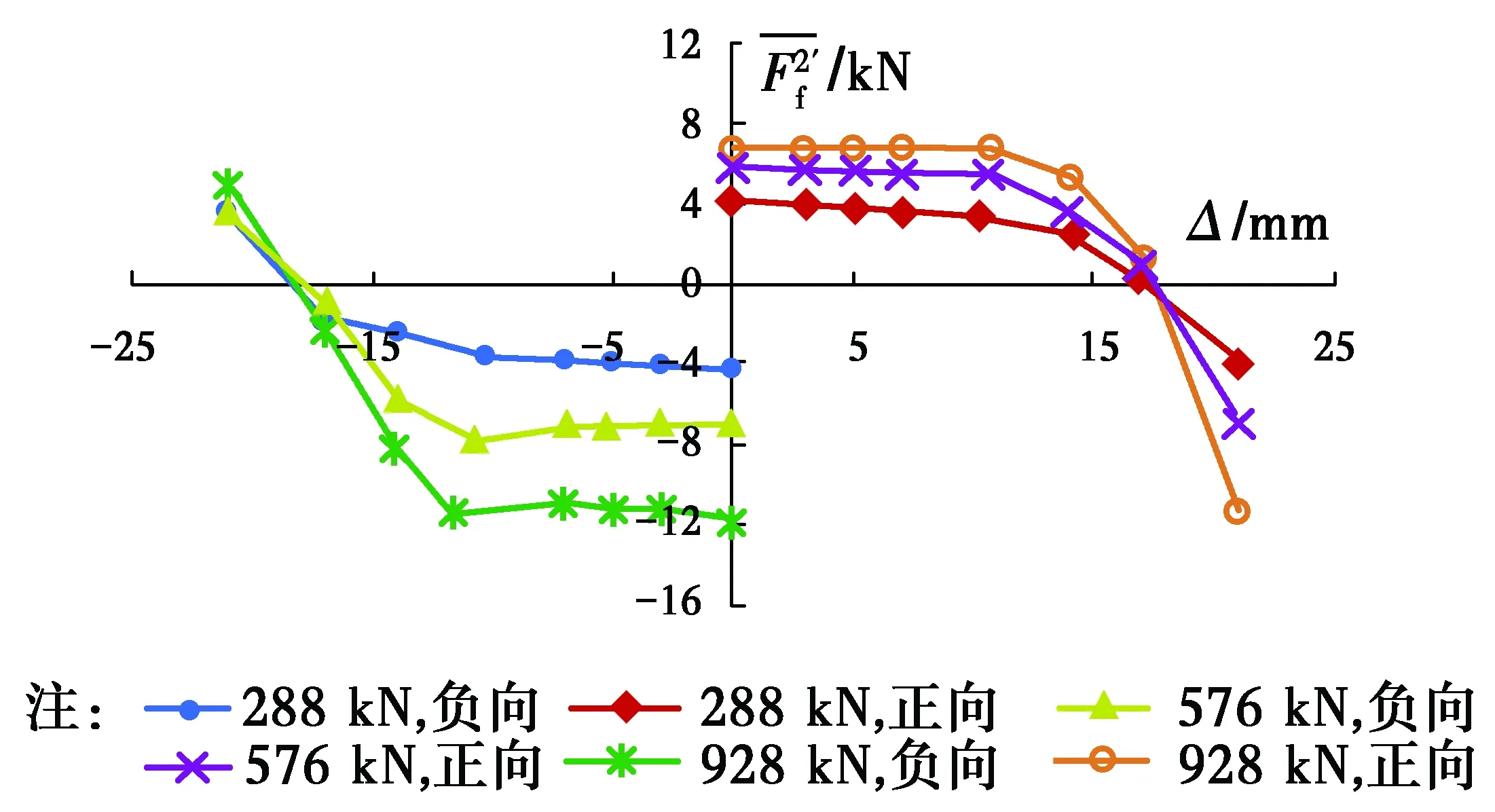
图15 试件GZ-1卸载段摩擦力平均值Fig.15 Average friction force of specimen GZ-1

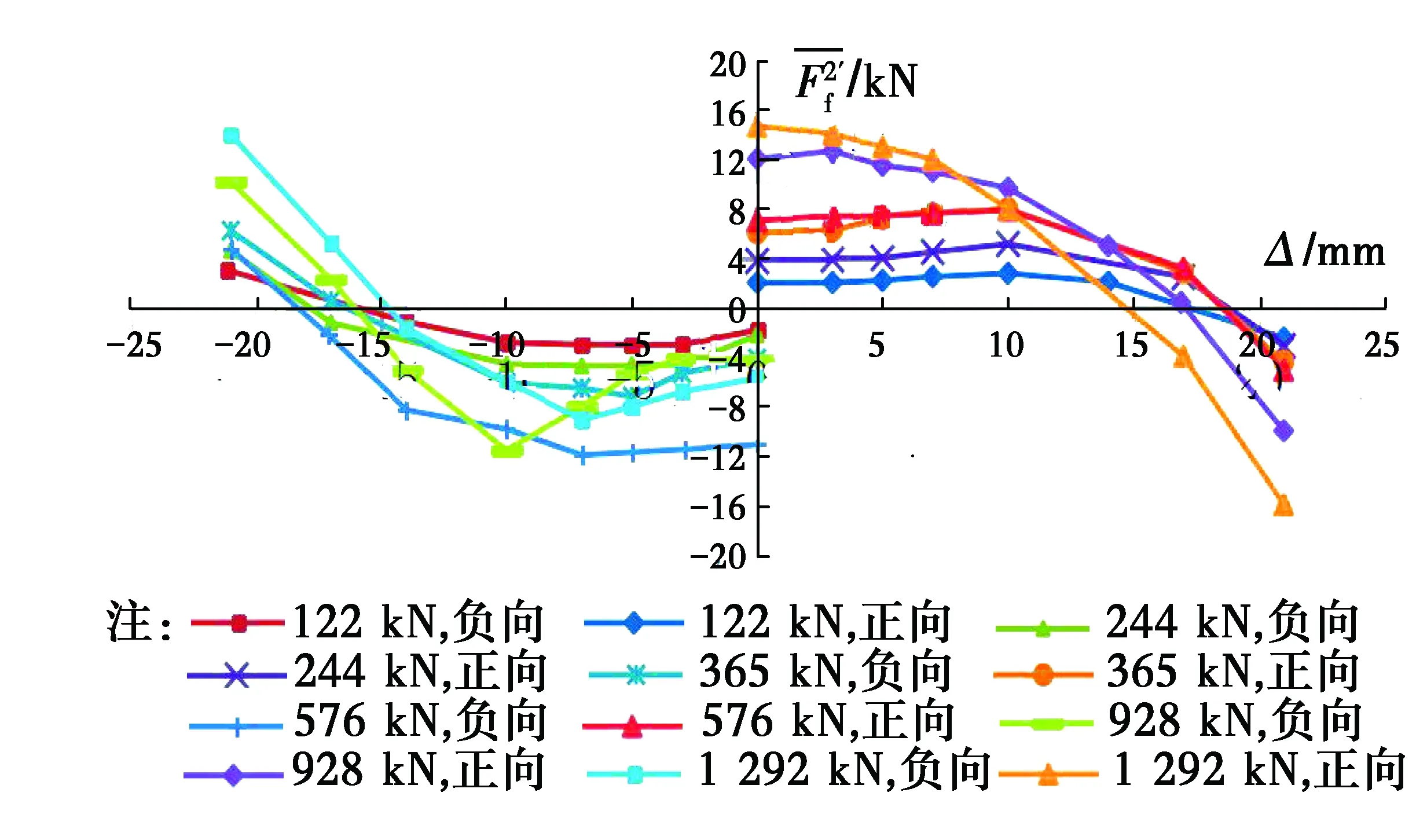
图16 试件GZ-2卸载段摩擦力平均值Fig.16 Average friction force of specimen GZ-2

图15、图16表明，各轴力作用下不同加载幅值点的卸载段摩擦力平均值与图14规律类似，即卸载段摩擦力仍随轴力的增大而增大。

以上分析结果表明，即使卸载段的柱顶位移相同，在不同位移幅值循环下其摩擦力会明显不同(见图14)，难以对各循环的卸载摩擦力平均值进行准确定量。

由于卸载摩擦力的稳定段即等于加载摩擦力，且卸载阶段摩擦力对修正试验结果较为次要，对其计算方法暂不深入分析。

图17表明，不同柱顶位移点的μf接近，柱顶位移对轴力加载装置引起的摩擦力影响较小。

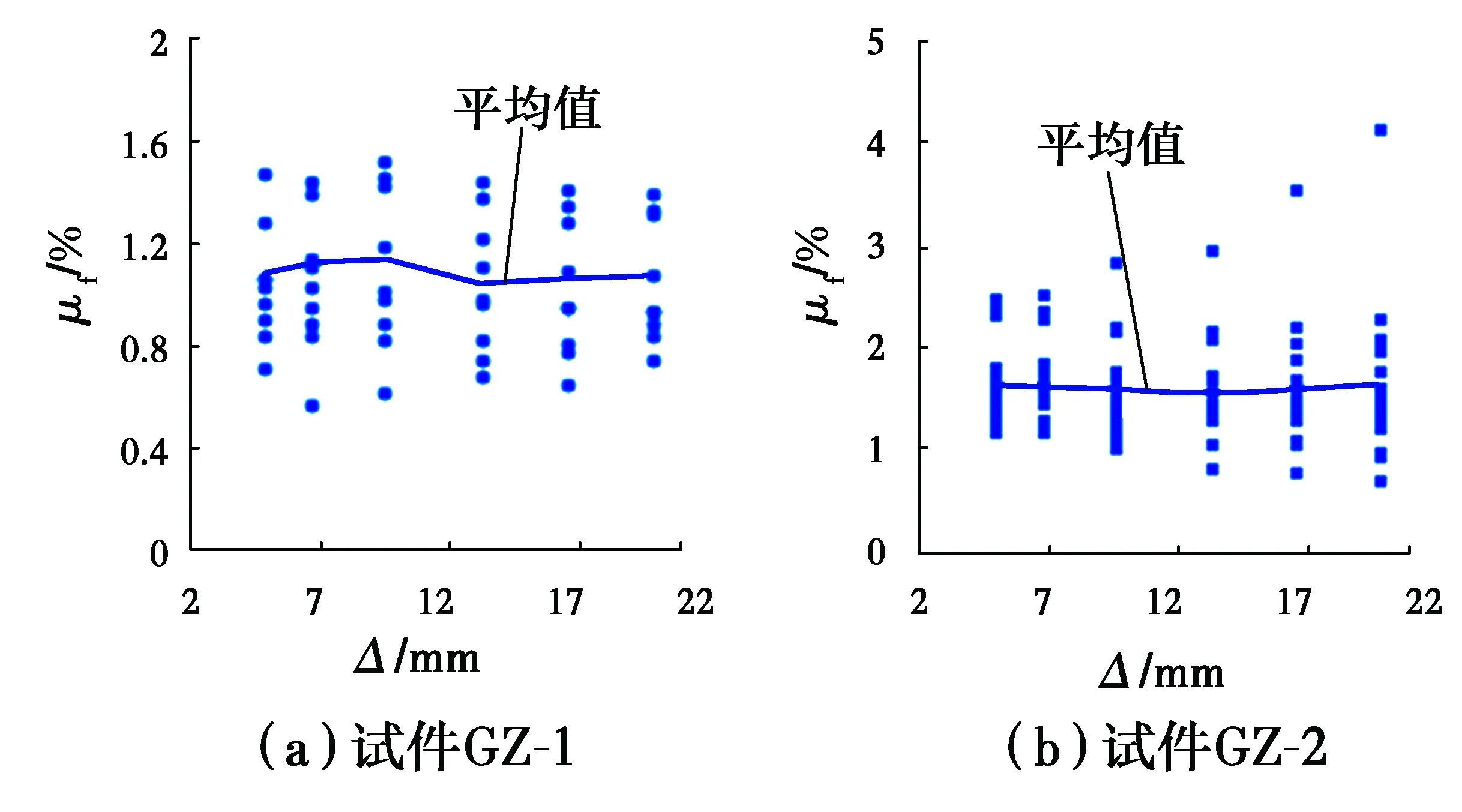
图17 各试件摩擦系数平均值与柱顶位移关系Fig.17 The relationship between friction coefficient average and displacement of

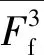
图18表明，轴力加载装置引起的摩擦力主要与轴压力N有关。随着N增大，Ff增大、μf减小，且最大Ff、最小μf均趋于较稳定取值；相同N作用下Ff在一定范围内变化，离散性不大；对于试件GZ-2、GZ-1采用的试验装置，μf可取约0.75%～2.45%。

图18 各试件轴压力与摩擦系数关系Fig.18 Relationship of axial force and friction

3 摩擦力对RC柱试验结果的影响

根据试件GZ-2、GZ-1的分析结果确定μf之后，由于采用的试验加载装置相同，可对文献[16]中2个RC柱试件SC-5(轴压比0.1)和SC-6(轴压比0.3)的P-Δ曲线试验结果(FN的修正已完成)进行摩擦力修正。

取与试件SC-5、SC-6轴压力对应的μf平均值对上述两RC柱的水平力测量结果FP进行修正。RC柱SC-5的目标轴力为365 kN，按图18可取μf为1.45%，对应的Ff为5.3 kN；柱SC-6目标轴力为928 kN，其μf可取为1.325%(见图18)，对应的Ff为12.3 kN。

考虑摩擦力修正后的试验结果对比如图19所示。

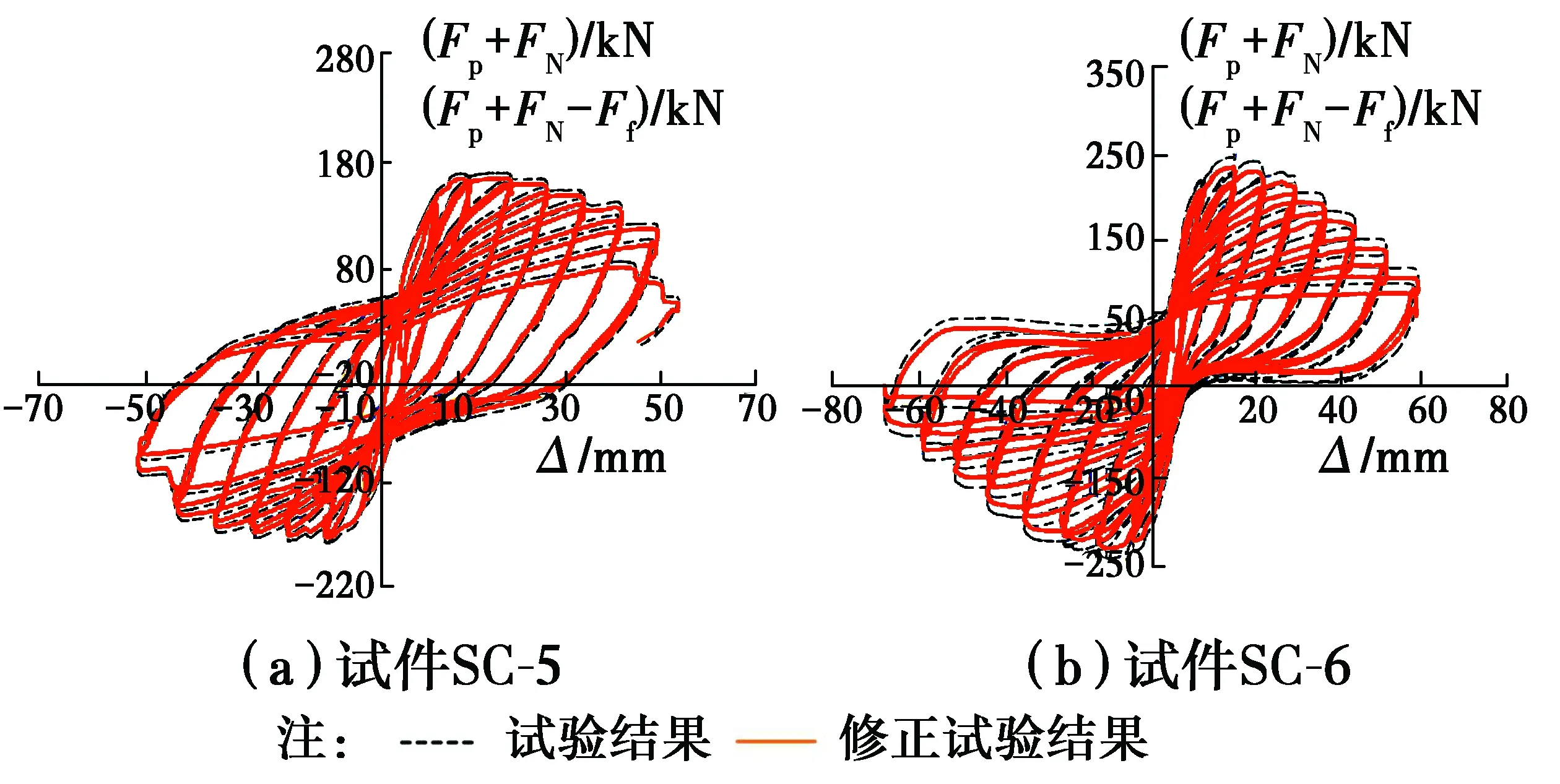
图19 摩擦力对RC柱P-Δ曲线的影响Fig.19 The effect of friction on P-Δ

图19表明，试件SC-5、SC-6的轴压力不同，轴力加载装置引起的Ff分别约为最大水平力实测结果的3.06%、5.27%。

轴力加载装置引起的摩擦力的大小、方向在卸载阶段均发生改变，规律较为复杂。因采用简化方法，图19中摩擦力修正后的水平力在卸载段(峰值点附近为摩擦力过渡段)存在误差。

4 结论

基于型钢柱试件弹性阶段的低周反复试验，结合精细有限元分析模型，建立了一种量化轴力加载装置所引起摩擦阻力的计算方法，得到以下主要结论：

1)在低周反复试验中，轴力加载装置将引起摩擦阻力，该摩擦力主要与轴压力大小有关，试件顶部水平加载位移的影响较小。

2)随着轴压力增大，轴力加载装置引起的摩擦力增大、相应的摩擦系数减小，最大摩擦力、最小摩擦系数趋于较稳定的取值。该试验的轴力加载装置的摩擦系数可取0.75%～2.45%。

3)轴力加载装置的摩擦系数还与钢轴承、钢铰上下摆铰孔接触面的光滑程度、制作工艺等有关，也与接触位置的随机性有关。

4)对于轴压力为350～900 kN的RC柱，该装置的摩擦力引起的水平力测量误差约为5～13 kN。