钢骨-组合L形钢管混凝土柱的轴压承载力
王博, 赵均海, 张冬芳, 马康凯
(长安大学 建筑工程学院,西安 710061)
钢管混凝土柱凭借其较高的承载力以及良好的抗震性能,越来越多地应用于建筑结构中。随着研究的不断深入,为了使不同位置柱的布置更加合理,提出了异形钢管混凝土柱(T形、L形、十字形)[1-3]。异形钢管混凝土柱采用边柱T形、角柱L形、中间柱十字形的方式广泛应用于中高层建筑结构,此类布置方式能有效避免柱阴阳角的出现,提高建筑的使用面积。随着现代结构向大跨度、大开间、重载方向发展,为提高异形钢管混凝土柱的承载力,提出将异形钢管混凝土柱中内置型钢钢骨组成内置钢骨的异形钢管混凝土柱,两者的结合将更加有效地发挥各自的特点。
学者们已经对异形截面钢管混凝土柱轴压性能进行了大量研究。Xiong等[4]对通过垂直双钢板连接的L形钢管混凝土柱进行了轴压试验,研究了柱的破坏模式、荷载-变形关系、应变分布、延性和强度指标;陈雨等[5]对T形钢管混凝土短柱进行了轴压试验研究,考察了无加劲措施T形钢管混凝土柱的变形特征、破坏模式和承载能力;Chen等[6]对6组L形钢管混凝土短柱和一组L形钢管空心短柱进行了轴压试验,描述了试件的非线性损伤过程和破坏模式,进行了结构参数对承载力的影响研究;雷敏等[7]基于单双向偏心受压试验结果,建立了纤维模型程序,分析其承载力的本构模型,在验证本构模型合理性的基础上,对T形钢管混凝土柱轴压稳定性能进行了参数研究。以上对异形钢管混凝土柱轴压承载力的研究表明异形钢管混凝土柱的合理性与适用性,但阴角易发生屈曲,重载下延性不足,混凝土斜裂缝的产生使得外包钢管对核心混凝土约束下降等问题依旧未得到解决,从而提出了内置钢骨的组合异形钢管混凝土柱。目前,对于内置钢骨的组合异形钢管混凝土柱轴压承载力研究,能够查阅到的研究文献还比较有限,宋鑫[8]通过对内置钢骨的组合L形截面钢管混凝土短柱轴心受压试验,研究了其破坏形态、荷载-位移曲线特征、各参数对其轴压力学性能的影响。杜国锋等[9-10]在试验基础上考虑钢管对核心混凝土的约束效应,依据数据拟合,提出了内置钢骨L形、T形钢管混凝土短柱的承载力公式。对于内置钢骨的组合异形钢管混凝土柱轴压承载力,部分研究主要以试验为主,所提出的承载力公式大多是从试验数据回归分析或简化计算得到,理论依据不够明确,不具备推广性;而部分研究所提出的承载力计算公式[10],在考虑钢管对混凝土的约束时,未合理考虑组合异形截面钢管的约束效应,同时,未考虑核心混凝土侧向约束对中心钢骨抗压强度提高的影响。
鉴于以上研究中存在的问题,本文以内置钢骨的组合L形钢管混凝土柱为研究对象,将组合L形短柱分为一个矩形钢管和一个方形钢管。考虑宽厚比对钢管纵向应力及环向应力的影响,将钢管长短边非均匀约束等效为环向均匀约束,引入混凝土强度折减系数,考虑侧向约束折减。基于统一强度理论,分别推导核心混凝土和钢骨的承载力公式,并建立钢骨-L形钢管混凝土短柱轴压承载力计算式。在此基础上,参考钢结构设计规范,提出轴压中长柱的承载力计算公式,为钢骨-组合L形钢管混凝土柱轴压承载力提供了理论依据。
1 统一强度理论
统一强度理论是俞茂宏[11]在1991年提出的,考虑了中间主应力对材料破坏的影响,适用于各种不同材料。具有简单而统一的数学表达式,清晰合理的物理概念和统一的力学模型,能够吻合学者们所得出的不同材料的大量试验结果,其数学表达式为
(1a)
(1b)
(2)
式中:F、F′为主应力强度理论函数;σ1、σ2、σ3分别为3个主应力;σt、σc、τs分别为材料的拉伸、压缩、剪切屈服应力;α为材料拉压强度比;b为反映中间主切应力以及相应面上的正应力对材料破坏影响程度的系数。
2 钢骨-组合L形钢管混凝土短柱轴压承载力计算
2.1 钢骨-组合L形钢管混凝土短柱轴心受压破坏机理
钢骨-L形钢管混凝土柱在轴压状态下,钢管、混凝土与钢骨共同承担轴向荷载作用。杜国锋等[10]试验研究表明,在加载初期,钢管对核心混凝土的约束较小,钢管、混凝土与钢骨均处于各自单独工作的弹性阶段。随着轴向压力的不断增大,钢管和钢骨纵向应变、钢管横向应变呈非线性增长,此时,钢管处于轴向受压、环向受拉状态。混凝土的横向变形加大,钢管对混凝土起到约束作用,核心混凝土受到钢管与钢骨的双重套箍作用,处于三向复杂应力状态下。随着加载的进行,达到极限荷载时,钢管和钢骨的应变开始迅速增长,钢管对混凝土的约束明显增强,试件各面微鼓变大,在矩形钢管的长边,钢管局部向外鼓出较其他各边更为明显。因此,本文依据轴压破坏机理,合理考虑钢管所处应力状态及对核心混凝土的约束作用,对轴压短柱极限承载力进行分析。
2.2 钢管宽厚比对环向及轴向应力的影响
Ge等[12]研究表明,钢管宽厚比是影响钢管混凝土试件承载力的主要因素,在轴向压力作用下,钢管处于轴向受压、径向受压、环向受拉的三向应力状态下,而径向受力相比环向与轴向较小,可忽略其影响。故基于VonMises屈服准则,当R>0.85时(R为钢管长短边宽厚比参数),认为钢管长边发生局部屈曲破坏;当R≤0.85时,可不考虑试件局部屈曲。利用文献[12]的研究成果,考虑在L形钢管混凝土柱中钢管宽厚比对环向及轴向应力的影响,计算公式为
(3)
当R>0.85时
(4)
(5)
当R≤0.85时
fa=0.89fy
(6)
fsr=-0.19fy
(7)
式中:B为钢管边长;Es、ν为钢管的弹性模量、泊松比;fa、fsr分别为钢管轴向抗压强度、环向抗拉强度。
2.3 钢管等效侧向约束力作用
核心混凝土分为有效约束区和非有效约束区,有效约束区混凝土抗压强度高于非有效约束区,非有效约束区所受的侧向压力是不均匀的[13]。根据组合L形特点,假定核心混凝土有效约束区的边界线为二次抛物线,如图1所示,对有效约束区和非有效约束区进行划分。

图1 横截面核心混凝土有效约束区Fig.1 Effectively confined concrete of


图2 钢管受力示意图Fig.2 Schematic diagram of the force of a steel
由平衡条件,得矩形钢管约束应力为
(8)
(9)
方钢管约束应力为
(10)
(11)

考虑到有效约束区较非有效约束区约束力强,依据面积占比,核心混凝土有效约束系数为
(12)
(13)
式中:θ1、θ2、θ3为约束界限边切角,考虑到长边和短边对核心混凝土的约束作用不同,采用龙跃凌等[15]基于试验数据所提出的公式。
(14)
(15)
(16)
(17)
(18)
(19)
式中:fy为钢管的屈服强度;ζ1、ζ2、ζ3分别为θ1、θ2、θ3的约束界限边切角系数,其中θ1、θ2、θ3的计算公式适用于长宽比a/b为1.0~2.0,宽厚比b/t为20~50的矩形钢管混凝土。
赵均海等[16]将方形钢管混凝土柱按面积相等等效为圆钢管混凝土柱,依据厚壁圆筒理论,在厚壁圆筒环向应力屈服条件下,得到侧向约束应力,且承载力公式与试验数据吻合较好。借鉴文献[16]中的方法,依据面积等效原则,将矩形混凝土等效成圆形混凝土。同时,按照侧向约束力相等原则,考虑钢管环向应力未达到屈服,将钢管各边侧向均匀约束等效为圆形钢管均匀约束,使得核心混凝土处于常三轴受压应力状态下,从而使得0>σ1=σ2=σr>σ3。
依据面积等效原则,将矩形混凝土等效成圆形混凝土,故
(20)
依据面积等效原则,将方形混凝土等效成圆形混凝土,得
(21)
式中:t为钢管壁厚;R1、R2分别为矩形和方形混凝土等效为圆形混凝土的半径。
可得到
(22)
(23)
依据侧向约束力等效原则,可得
(24)
(25)

将式(8)、式(9)、式(22)代入式(24),得
(26)
将式(10)、式(11)、式(23)代入式(25),得
(27)
考虑环向应力未达到屈服,依据钢管环向应力式(5)、式(7),可得
(28)
(29)
将式(28)、式(29)分别代入式(26)、式(27),得
(30)
(31)
2.4 核心混凝土的轴压强度

σ3=fc+kσr
(32)
考虑到矩形钢管约束力不如等效圆钢管约束力强,引入折减系数γu,得
(33)
(34)

将式(30)、式(31)分别代入式(33)、式(34),可得
(35)
(36)
2.5 钢骨承载力

(37)
式中:fst为钢骨拉伸屈服强度;α为钢骨材料拉伸强度fst和压缩强度极限fsc的比值。
公式中取压为正,拉为负,根据式(37)可得
fs1=σ3=σr+fsc
(38)
(39)
式中:fs1、fs2分别为矩形钢管钢骨和方形钢管钢骨的抗压承载力;fsc为钢骨抗压强度。
将式(30)、式(31)分别代入式(38)、式(39),得
(40)
(41)
2.6 L形短柱轴压承载力计算
组合短柱的轴压承载力由3部分组成,分别是钢管纵向承载力、受约束混凝土所提供的承载力以及中心钢骨所提供的承载力。轴压短柱承载力公式为
Nu=Nu1+Nu2
(42)
Nu1=fyt1At1+fc1Ac1+fs1As1
(43)
Nu2=fyt2At2+fc2Ac2+fs2As2
(44)
式中:Nu为L形短柱承载力;Nu1、Nu2分别为矩形和方形钢骨钢管混凝土短柱承载力;fyt为钢管压应力,当短柱达到极限承载力时;At、Ac、As分别为钢管的承压面积、混凝土的承压面积以及钢骨的承压面积。fyt按照式(7)、式(9)算得。
将式(5)、式(35)、式(40)代入式(43),可得
(45)
将式(6)、式(36)、式(41)代入式(44),可得
(46)
将式(45)、式(46)代入式(42),可得
Nu=fyt1At1+fyt2At2+Acfc+Asfsc+
(47)
3 钢骨-组合L形钢管混凝土中长柱轴压承载力计算
3.1 中长柱稳定系数计算公式
根据中国相关规程,包括GB 50936—2014、CECS28:2012、DL/T—5085—1999中对于中长柱承载力的计算,普遍采用短柱轴压承载力乘以稳定系数。本文采用式(47)所得到的短柱承载力计算结果再乘以稳定系数,确定长柱承载力,计算式为
NL=φNu
(48)
(49)
相对长细比公式为
(50)
式中:Nu为短柱承载力,按照式(47)计算;L0为柱的计算长度;Et、Es、Ec分别为钢管、钢骨、混凝土的弹性模量;It、Is、Ic分别为钢管、钢骨、混凝土的截面最小形心惯性矩,计算公式由3.2节给出;γ为混凝土刚度折减系数,EcIc所占比重较小,故取γ=1。
3.2 L形钢骨-钢管混凝土柱最小形心主惯性矩的确定
组合异形柱形心的确定对于轴压承载力的研究有重要的意义,L形钢骨-钢管混凝土柱由钢管、混凝土以及钢骨组成,三部分的材料不同,从而刚度以及弹性模量不同,故其形心不能按照外形确定。本文按照刚度换算截面法来确定形心,将混凝土的面积按照等刚度原则换算成钢材的面积,然后分别和矩形和方形两部分的钢管面积、钢骨面积相加,组成形心不变、刚度相等的两部分面积A1和A2,建立坐标如图3,利用形心公式计算L形钢骨-钢管混凝土柱的形心。
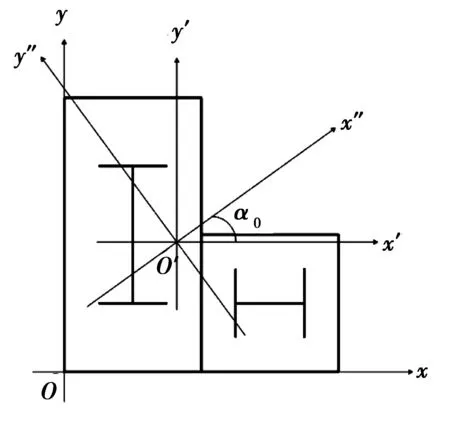
图3 L形组合柱形心Fig.3 L-shaped Composite column

(51)
(52)
从而确定形心位置O′点,以O′为中心点建立X′-Y′坐标系,分别计算钢管、混凝土、钢骨的形心惯性矩,即Ixt、Ixc、Ixs、Iyt、Iyc、Iys、Ixyc、Ixyt、Ixys,可得形心惯性矩及惯性积为
Ix′=Ixc+Ixt+Ixs
(53)
Iy′=Iyc+Iyt+Iys
(54)
Ix′y′=Ixyc+Ixyt+Ixys
(55)
故可求得形心主惯性轴转动角度的正切值
(56)

(57)
(58)
式中:Ix1、Iy1为主惯性矩。
4 理论公式验证及参数分析
4.1 理论公式验证

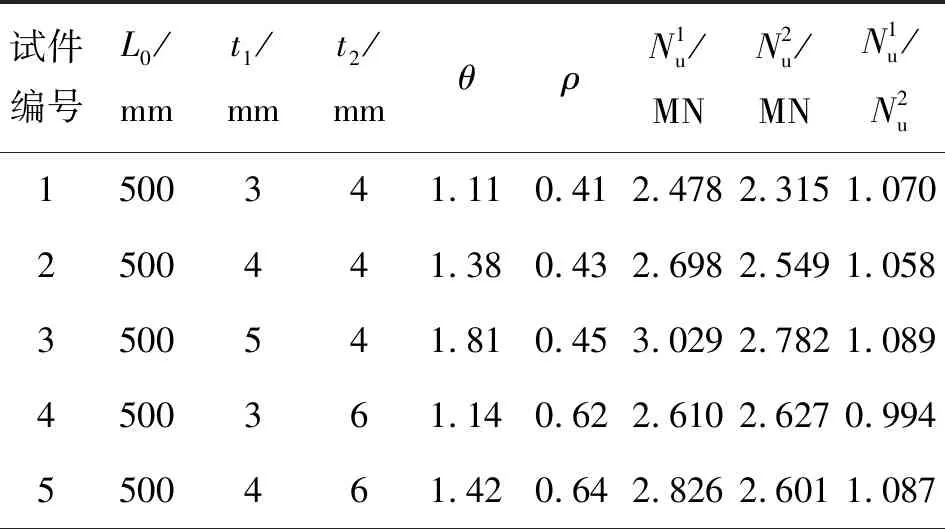
表1 L形短柱承载力计算与试验值比较Table 1 Comparisons of L-shaped short column between calculation results and experiment results of bearing capacities

续表1
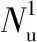
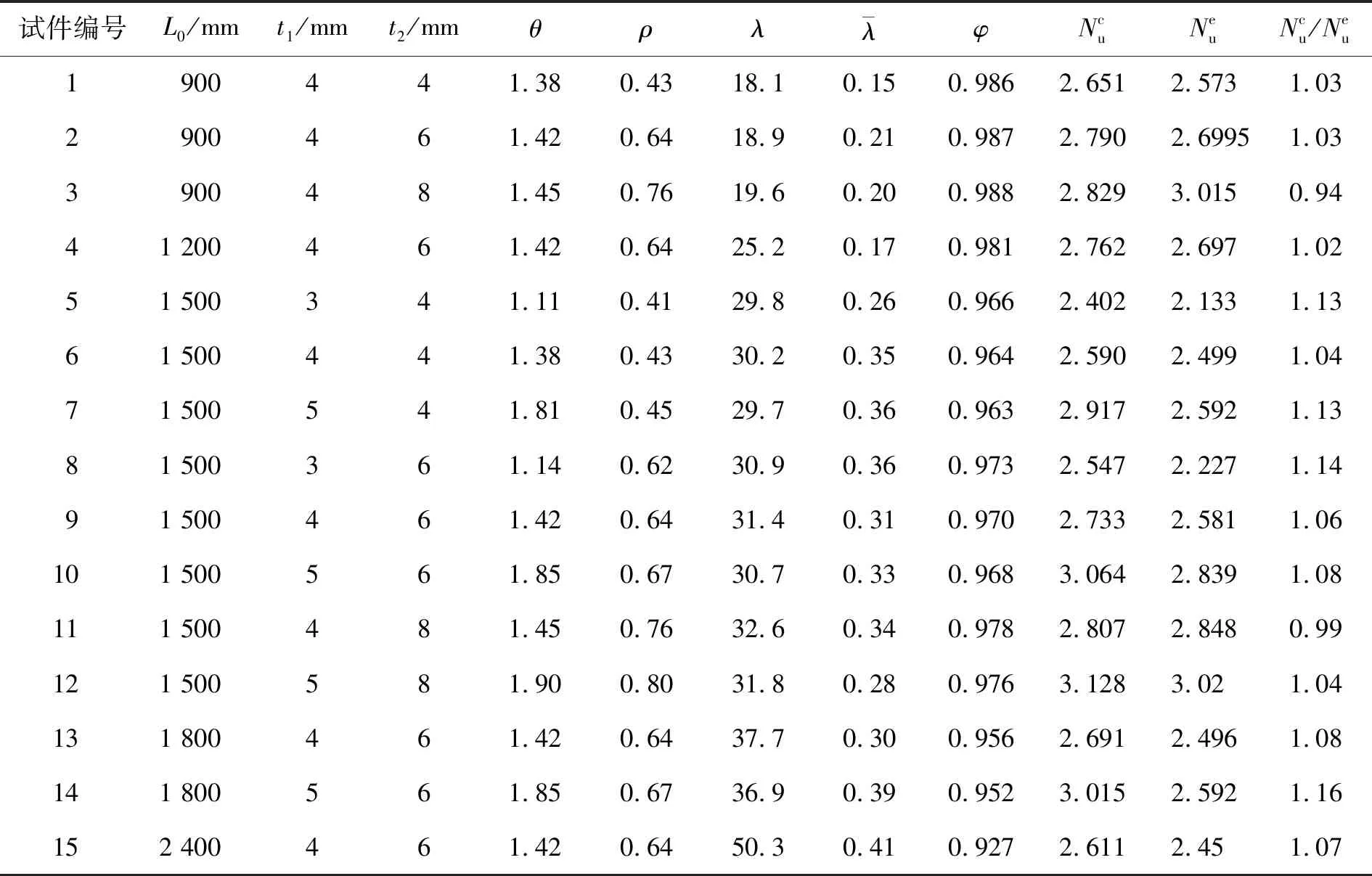
表2 L形中长柱承载力计算与试验值比较Table 2 Comparisons of L-shaped long column between calculation results and experiment results of bearing capacities
4.2 影响因素分析
4.2.1 混凝土k的影响 对于钢管混凝土,k=1.5~3.0,考虑钢骨对于混凝土套箍作用的提高,取k=3.0。取短柱3号试件(见表1),其他参数不变,系数k在1.5~3.0变化时,由图4可知,随着k的增长,短柱轴压承载力随之呈线性增长,但k值也不可能无限增大,它与材料的轴压性能有关。k的增大表明混凝土内摩擦角增大,抗拉强度增强。
对于内置钢骨的钢管混凝土而言,由于钢骨的存在,一方面有效延缓了混凝土斜裂缝的产生,使核心混凝土的抗剪切能力提高;另一方面,外包钢管对核心混凝土的套箍作用得以提高,相应地增大了混凝土内摩擦角,使得该类异形组合柱承载力提高。在k=3.0时,所得承载力与试验数据吻合较好。
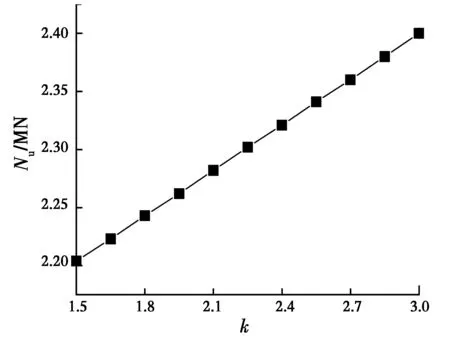
图4 k对承载力的影响Fig.4 Effect of k on the bearing
4.2.2 钢骨材料拉压比α的影响 组合短柱轴压承载力受钢骨影响较大,而钢骨的承载力主要与拉压比α、含骨率ρ有关。但对于高强钢材,考虑钢材的SD效应,材料拉压比不再等于1,对于韧性金属材料,α一般为0.77~1.00[21-22](如AISI 4330,α≈0.87; AISI 4320,α≈0.92; AISI 4310,α≈0.95[23])。图5为基于式(47)得到的钢骨-组合L形钢管混凝土短柱轴压承载力随材料拉压比α和含骨率ρ的变化曲线。由图5可知,随着拉压比α的增加,轴压承载力不断降低;当保持α不变,随着含骨率ρ的不断增加,L形组合结构承载力不断增大。
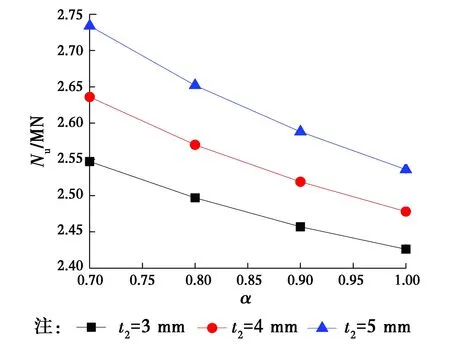
图5 拉压比α、含骨率与承载力Nu的关系Fig.5 Ralationship of bearing capacity and pull pressure ratio α、osseous rate
由图5可以看出,拉压比α对短柱承载力的影响相对较小。当拉压比取值相差超过0.3时,对于承载力的影响接近3%,故在计算钢骨承载力时,可忽略拉压比的影响,但对于材料拉压比α较小时,考虑其影响能够取得更加精确的承载力计算值。钢骨含骨率对短柱承载力影响较大,当其他参数不变,钢骨厚度增加1 mm,对承载力的影响超过5%。
5 结论
1)基于统一强度理论,对钢骨-组合L形钢管混凝土短柱以及中长柱轴压受力性能进行了理论研究,分别建立了其轴压承载力计算公式,并与试验数据进行对比验证,吻合较好,从而验证了本文研究方法的正确性,为内置钢骨的组合异形钢管混凝土柱轴压承载力计算提供了参考。
2)随着k值的增大,即混凝土内摩擦角不断增大,短柱轴压承载力增大,而钢骨的存在能够有效提高对混凝土的套箍作用,提高混凝土的内摩擦角,从而取得较高的承载力。
3)材料拉压比α对短柱承载力具有一定影响,随着材料拉压比α的增大,承载力不断降低,对于拉压比较小的钢材,考虑拉压比能够取得更加精确的承载力计算值;含骨率ρ对短柱承载力有较大的影响,随着含骨率ρ的增加,短柱承载力逐渐增大。
4)所得计算式能充分考虑钢骨拉压比的不同,具有广泛应用性;合理考虑钢骨组合L形钢管混凝土柱的划分方法、承载力影响因素以及应用统一强度理论,为工程应用提供了相应的理论依据。

