基于Wilcoxon的仿射投影算法

李琳琳，郭 莹

（沈阳工业大学信息科学与工程学院,沈阳110870）

1 引言

最小均方算法（Least Mean Square,LMS）因其形式简单、鲁棒性强而被广泛应用于未知线性系统的辨识。然而在许多实际环境中，由于自然因素和人为因素的影响，噪声通常表现出强冲击性，即存在异常值，这并不符合高斯分布。Majhi等人提出了通过Wilcoxon范数代替欧式范数作为代价函数，以改善LMS对异常值的失调性能。在这种方法中，不是将误差项的平方最小化，而是将与每个误差值相关的等级最小化。等级是通过对一个数据块获得的误差值进行排序来计算的。这种强大的技术已被应用于系统识别[1-3]。然而，当输入信号相关性较高或者输入信号是有色信号时，LMS算法的收敛速度会明显降低。为了克服这一问题，Ozeki和Umeda提出仿射投影算法（Affine Projection Algorithm,APA）。但是当噪声呈现非高斯脉冲分布时，经APA得到的解将不是最优解[4]。针对非高斯噪声干扰问题，S.J.Ban等人提出了基于Wilcoxon范数的仿射投影算法（Wilcoxon Affine Projection Algorithm,WAPA），通过最小化加权Wilcoxon范数来克服APA算法的不足[5]。

根据Sign-Sign Wilcoxon比Sign Wilcoxon算法具有更好的收敛速度这一思想，可认为Sign-Sign Wilcoxon仿射投影算法（Sign-Sign WAPA）相比于Sign Wilcoxon仿射投影算法（Sign WAPA）在存在异常值时具有更快的收敛速度[6]。但是Sign-Sign WAPA的步长是固定的，在参数选择和收敛速度方面有一定的局限性。故此，提出变步长符号-符号仿射投影算法（Variable Sign-Sign WAPA），通过引入步长函数，可很好地解决这一问题[7]。

对 APA、WAPA，Sign WAPA，Sign-Sign WAPA，Variable Sign-Sign WAPA进行综合比较分析。仿真研究表明，在具有高相关输入数据和输出数据存在非高斯噪声的条件下，与其他算法相比，Variable Sign-Sign Wilcoxon APA具有更好的性能。

2 Alpha稳定分布

Alpha稳定分布是高斯分布的一种推广，非常适合描述带有脉冲性质的实际环境噪声[7]。Alpha稳定分布不存在闭合形式的概率密度函数，因此可用一般特征函数描述。对随机变量X，其特征函数可以描述为：

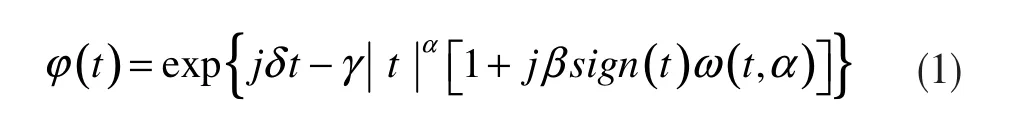
其中，

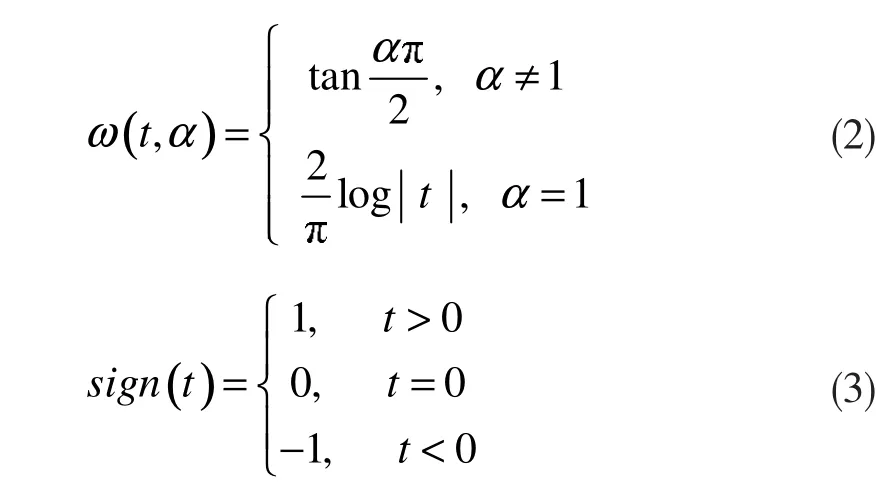
Alpha稳定分布的表现由四个参数α、β、δ、γ决定；其中α是特征指数，取值范围为0＜α≤2，决定着Alpha稳定分布脉冲性的强弱，当α=2时表示分布为高斯分布；β是对称参数，取值范围为-1＜β≤1，当β=0时为对称Alpha稳定分布或称SαS分布；δ为位置参数，取值范围为-∞＜δ＜∞；γ为分散系数，取值范围为γ＞0。α在不同取值条件下所对应的概率密度函数曲线如图1所示。

由图1可以看出当特征指数α=2时，SαS概率密度函数曲线与实质上均值为零且方差为2的高斯分布曲线保持一致。SαS分布概率密度函数的拖尾厚薄程度变化受α值的影响，随着特征指数α的减小，拖尾变厚，表现出更强的脉冲性。因此，SαS分布非常适合用来描述那些类似于高斯分布，却具有很强冲击性的非高斯分布。

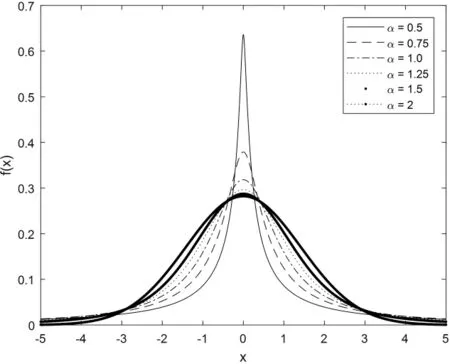
图1 特征指数α在不同取值下的概率密度函数曲线

3 Wilcoxon估计

在统计中，使用基于秩的Wilcoxon生成的线性回归器对异常值不敏感。对于线性最小二乘回归和线性Wilcoxon回归对异常值的鲁棒性的差异，可用以下示例进行比较。

示例由图2给出，其中包含20个数据样本点并存在30%的异常值。真实函数为y=10x+2。以最小二乘方法得到的回归线性方程为y=8.3395x+6.9395，而由Wilcoxon方法得到的结果为真实函数y=10x+2。回归结果亦如图2所示。

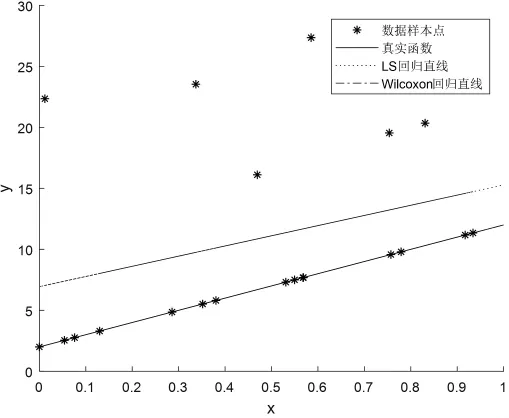
图2 最小二乘估计与Wilcoxon估计比较

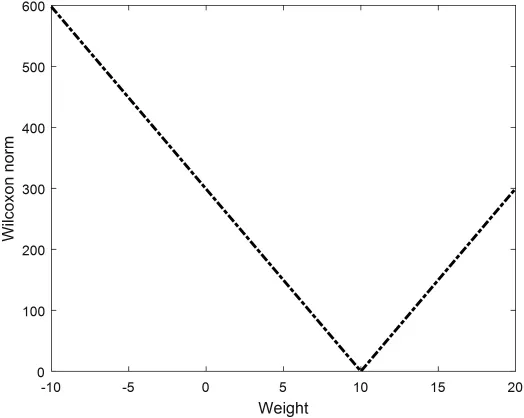
图3 函数关系 w ↦的曲线

4 Wilcoxon范数

Wilcoxon范数的定义需要一个单调递增的记号函数φ φ(( uu )):：[[00,,11]]→→Rℜ ，且满足：

其中，记号函数φφ被定义为：

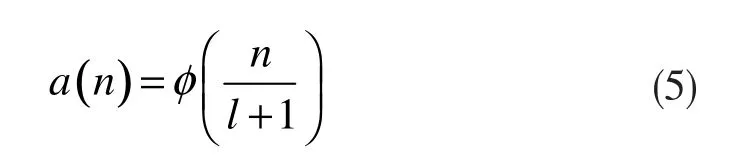
其中n=1,2,...,l。l为固定的正整数。

令向量v∈∈ℜRll， 则其Wilcoxon范数被定义为：

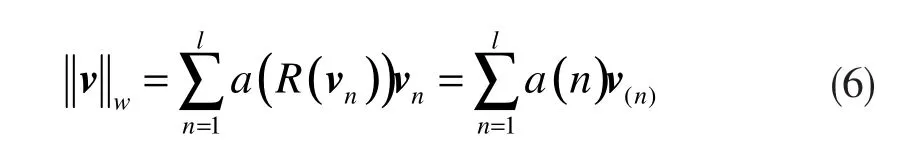
Sign Wilcoxon范数则为仅将记号函数前加入“符号”，定义为：

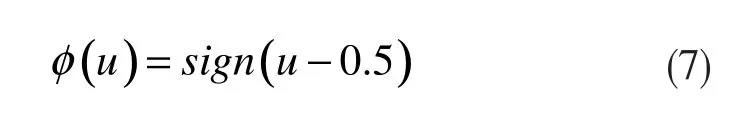
5 Wilcoxon APA算法

在数据重组中，将最后的L个输入信号向量写为如下的矩阵形式：

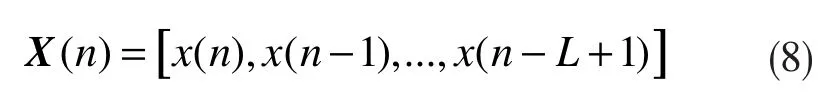
输出向量y(n)可以表示为：

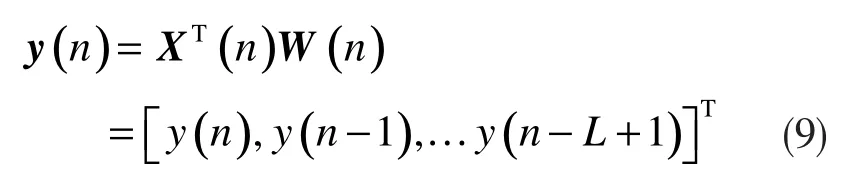
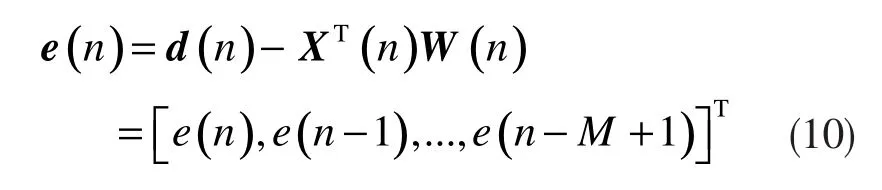
APA算法的权系数向量更新公式为：

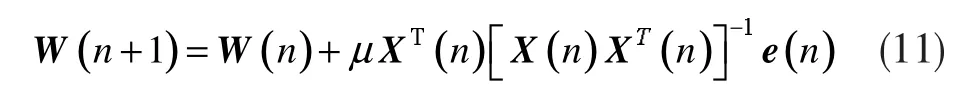
同时为了防止自相关X(n)XT(n)太小，算法中还可引入一个非常小的正整数，APA算法的权系数向量更新公式变为：

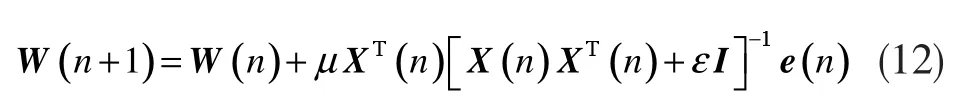
其中，ε是正则化因子，I为M×M的单位矩阵，εI是为避免对不满秩方阵求逆而添加的一个对角矩阵。

基于公式(12)，Wilcoxon范数APA的权系数更新公式可以写成：

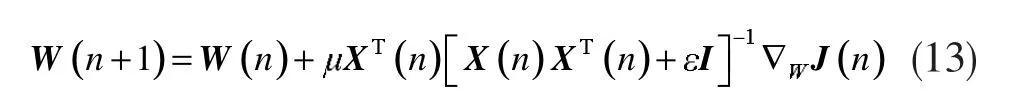
Wilcoxon APA算法的代价函数为：

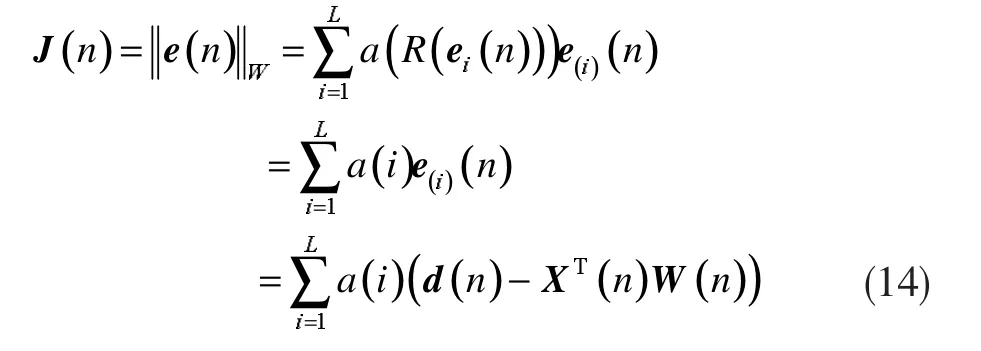
对代价函数J(n)关于W(n+1)求偏导，则：

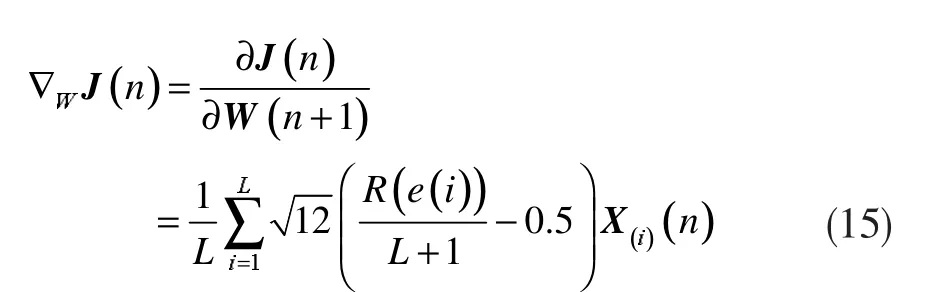
Wilcoxon范数APA算法的权系数更新公式为：

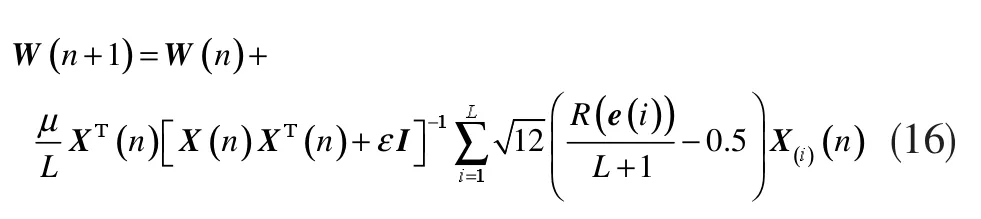
根据式 (7)、(16)，Sign Wilcoxon范数 APA 算法的权系数更新公式为：

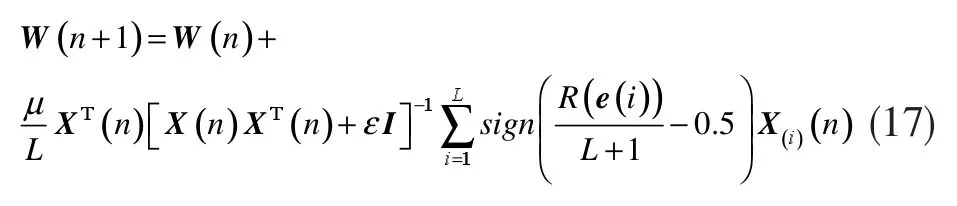
6 变步长Sign-Sign WAPA

在有异常值存在的情况下，设计一个能有效地估计其参数的模型。Wilcoxon范数和Sign Wilcoxon范数存在异常值时都能显现出良好的鲁棒性。与传统方法相比，Sign-Sign技术有更快的收敛速度。在Sign-Sign Wilcoxon方法中，误差向量和记号函数都用符号函数来表示。Sign-Sign WAPA算法的权系数更新公式为：

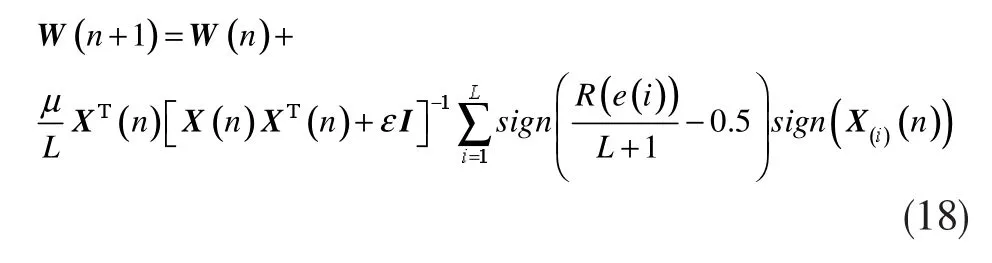
利用固定的步长参数μ描述权值更新方程，固定步长自适应算法仅能有效地跟踪缓慢运动的参数化，因此固定步长Sign-Sign Wilcoxon方法不能产生比变步长更好的结果。由于步长参数起着至关重要的作用，为了构造更加鲁棒的系统，应对自适应算法进行变步长改进。瞬时步长定义为：

其中，μi是在所提出的自适应算法中使用的瞬时步长值。Δμ定义为固定步长的初始值，S=X(n)e(n)，sp为s上一次迭代的值。最后的步长大小定义为：

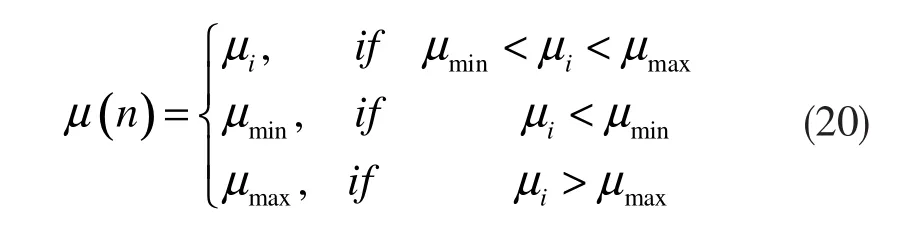
其中μmin和μmax定义为该算法的最小步长和最大步长，步长的大小可以在μmin和μmax之间选择。

至此Variable Sign-Sign WAPA算法的最终更新方程为：

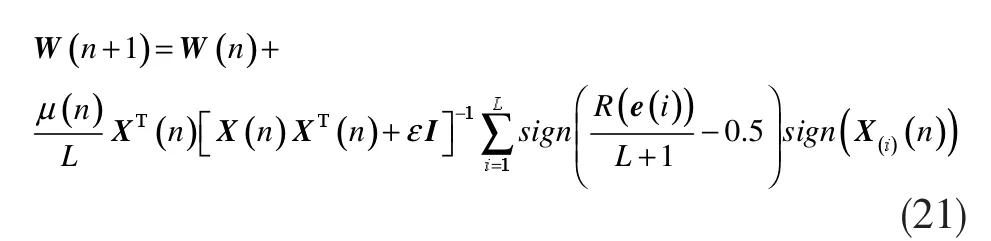
随后可将Variable Sign-Sign WAPA算法和其他算法在高斯噪声和非高斯噪声下进行对比验证。

7 实验仿真

为验证所提算法的收敛速度、稳态失调及其跟踪的性能，对几种相关算法用MATLAB进行仿真。算法的收敛性能是以归一化均方偏差（Normalized Mean Square Deviation,NMSD）的收敛曲线来评价的，定义为：

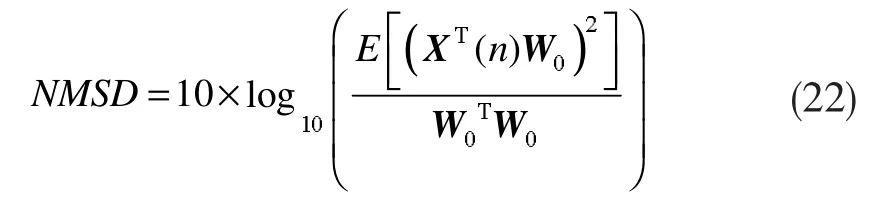
可见NMSD是对自适应滤波器与目标系统的逼近程度的度量。

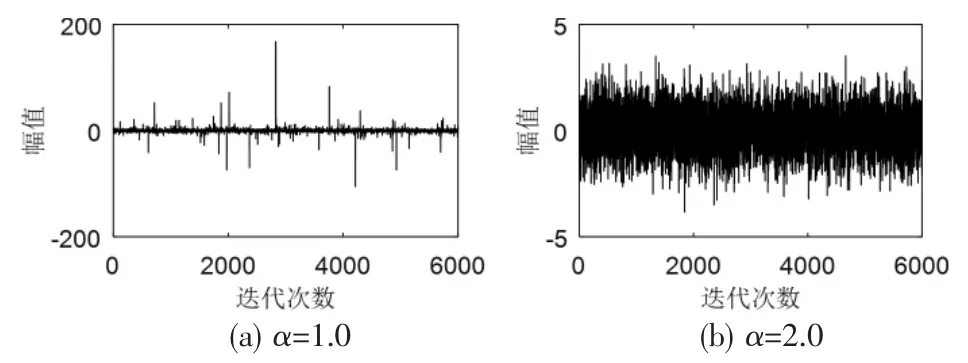
图4 不同高斯干扰条件下α稳定噪声

图5为APA、WAPA、SignWAPA、Sign-SignWAPA和Variable Sign-Sign WAPA在高斯噪声条件下的NMSD收敛曲线。

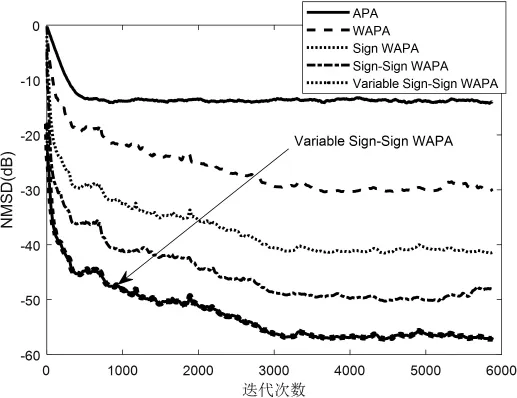
图5 高斯噪声下各算法的性能比较

由图中可见，当干扰噪声为高斯噪声时，所提的 Variable Sign-Sign WAPA比 Sign-Sign WAPA、Sign WAPA、WAPA、APA都要具有更快的收敛速度和较小的稳态失调。

图 6为 APA、WAPA、Sign WAPA、Sign-Sign WAPA和Variable Sign-Sign WAPA在非高斯噪声条件下的NMSD收敛曲线。

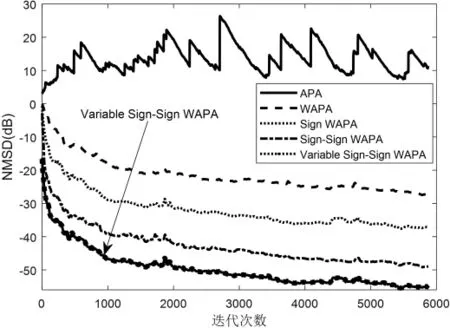
图6 非高斯噪声下各算法的性能比较

由图6可以看出，APA算法已经发散。所提Variable Sign-Sign WAPA和Sign-Sign WAPA算法的收敛速度较Sign WAPA和WAPA算法有极大改善，较Sign WAPA的稳态失调也改善了20dB左右。

图5和图6也同时验证了所提出的Variable Sign-Sign WAPA在干扰噪声为高斯噪声和非高斯噪声时相比于其他算法的优势，包括稳态失调，收敛速度和抗脉冲干扰性能。因此，所提的新算法技术对异常值具有较强的鲁棒性。

如图7所示，为在干扰噪声为非高斯噪声下提出新算法Variable Sign-Sign WAPA与WAPA、Sign WAPA、Sign-Sign WAPA各算法的跟踪性能仿真曲线。当迭代次数达到3000的时候，回声信道W变为-W。如图所示，提出的新算法Variable Sign-Sign WAPA和Sign-Sign WAPA算法在信道发生突变时，具有良好的跟踪性能。

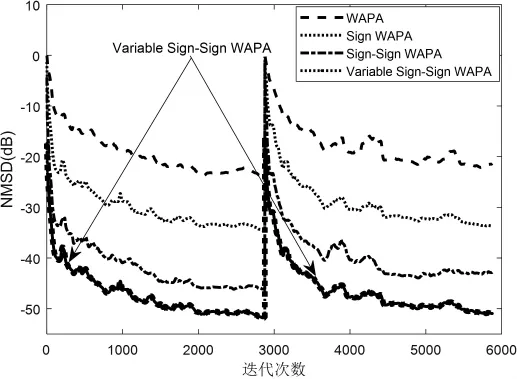
图7 非高斯噪声下各算法跟踪性能

8 算法在回声消除中的应用

在回声消除的真实场景中，远端输入信号一般是语音信号，有必要保证这种情况下算法的鲁棒性。将所提的Variable Sign-Sign WAPA算法应用到如图8所示的自适应回声消除系统中，与现有的APA、WAPA、Sign WAPA 及 Sign-Sign WAPA 算法进行比较。输入信号采用真实语音信号，波形如图9所示。其采样频率为8kHz，样本长度为480000。以此比较在非高斯噪声条件下各个算法的收敛性能。

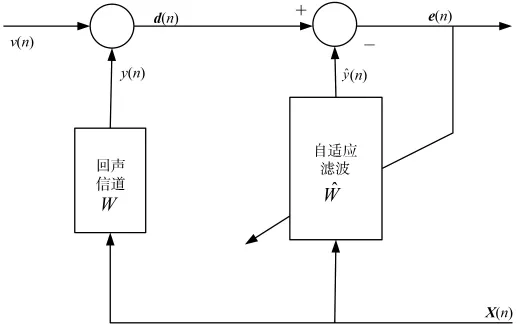
图8 自适应回声消除系统

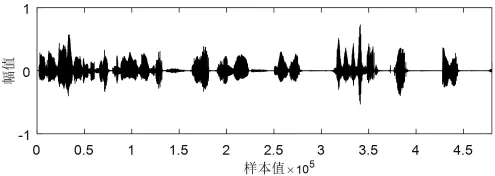
图9 某真实语音信号波形

如图8所示，X(n)是远端信号，即输入信号。v(n)是近端信号。表示回声信道W的估计值。当远端语音信号X(n)通过W产生回声信号y(n)，d(n)为麦克风获取的信号，也是自适应滤波器的期望信号。当自适应滤波算法处于稳态时，自适应滤波器的输出ˆ(n)即为回声信号估计值，将其从期望信号中减去即可实现回声消除。

各算法的收敛性能在非高斯噪声条件下的对比情况如图10所示。一方面所提的Variable Sign-Sign WAPA和Sign-Sign WAPA算法均表现出了对强脉冲干扰的鲁棒性；另一方面，在加入语音信号时，Variable Sign-Sign WAPA算法仍保持较快的收敛速度，而WAPA和Sign WAPA收敛变慢，稳态失调高，总体性能差。以此便可证明，所提新算法在语音信号状态下具有优越的性能，适用于回声消除的应用中。

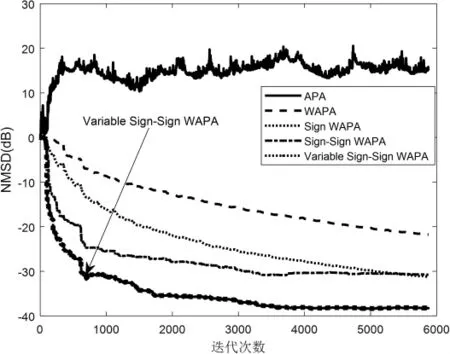
图10 非高斯噪声条件下的收敛性能

9 结束语

通过基于Wilcoxon范数作为代价函数，提出了一种新的变步长Sign-Sign Wilcoxon仿射投影算法。在高斯噪声干扰和非高斯噪声干扰下将APA、WAPA、Sign WAPA、Sign-Sign WAPA 和 Variable Sign-Sign WAPA进行比较。仿真结果表明，无论输入信号是有色信号还是语音信号，所提出的新算法比其他算法都具有较快的收敛性能和更低的稳态失调，并且在信道突变时，有着良好的跟踪性能，在系统中包含强脉冲干扰时，也能表现出很强的鲁棒性。