一种变权重k最近邻的室内外无缝定位算法*

李玉峰，张 佩，王宇鹏

（沈阳航空航天大学电子信息工程学院，沈阳110136）

1 引言

定位技术大体上可分为室内定位和室外定位两个大的方向。室外环境的定位技术主要以全球导航卫星系统（Global Navigation Satellite System,GNSS）为主，因其易用性和广泛覆盖性被广泛应用在户外定位中[1]，但由于卫星导航的固有特性，在室内或拥挤的市区环境下，无法提供定位服务。在室内定位方面，出现了众多的定位方案：WiFi、蓝牙、红外信标、超宽带（Ultra-Wide Bandwidth,UWB）等，在这些技术中UWB属于比较新颖的技术。由于UWB信号有很高的时间分辨率，很快在定位领域广受关注和研究。在文献[2]中，由克拉美罗下界可知，UWB的定位精度在厘米级。但由于其带宽很宽和功率小的特点，只适用于范围较小的室内环境，这在很大程度上限制了UWB在室外定位的发展[3]。

为了提供室内外全范围的定位服务，依靠单一的定位手段是无法实现的；而且在大面积和复杂的室内环境中，定位区域不止一个，因此如何在不同定位区域内实现流畅地软切换也是一个有待解决的问题[4]。为解决上面提到的这两个定位问题，提出一种基于GPS和UWB的无缝定位方案。该无缝定位方案是基于k最近邻算法实现了不同定位数据的融合，进而实现不同定位区域的软切换，同时也可实现定位数据的滤波，并在一定程度上抑制了非视距误差[5]。

k最近邻算法（kNN）是一种主要用于分类以及回归的非参数统计方法。当前在机器学习领域该算法已受到较为广泛的使用[6]，但在信息的融合以及定位方面，该法并未得到广泛关注和使用。

2 无缝定位系统的设计

在此定位方法中，把室外GPS定位区域及室内UWB不同的定位区域都看成是相同类型的定位区域，进行无差别地定位估计。因此室内外无缝定位切换和室内不同区域的软切换这两个问题就抽象为一个问题：如何处理所有接收的定位数据（UWB测距数据、GPS数据）并进行估计，从而得出一个最优解作为定位的估计点。这样在进行定位估计的同时就完成了不同定位区域的软切换。

采用权重可变的k最近邻算法[7]来解决上面提到的问题。把所有解算产生的UWB定位估计点以及GPS定位数据点看成是近邻点，并把前一状态的一步预测值作为参考点来与那些近邻点进行邻近判断。根据二维平面的欧式距离作为权重计算依据来得出k近邻范围内所有近邻点的加权平均值，把该值作为本次定位的估计值，并用于计算出下次定位估计中的一步预测值。不同定位模块（UWB或GPS）及相同定位模块的不同测量形式，如基于TOA（Time of Arrival）、TDOA（Time Difference of Arrival）等，经过初步的解算都可以产生二维平面上的坐标点，即所提到的近邻点为：

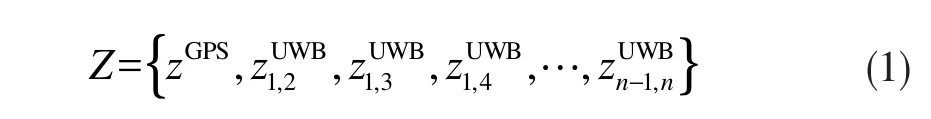
式中，上标代表近邻的定位数据来源，下标代表当前定位区域中双定位基站序号的组合，n代表最多基站数。

在决策阶段，采用的是权重决策机制，即根据不同近邻点的权重进行加权平均进而得出最后的定位估计点。因此问题进一步转换为如何动态地调整所有可能的定位近邻点的权重，在动态调整定位近邻点权重的过程中便实现了错误数据的剔除（包括定位多解的消除）和正确数据的融合，从而实现了不同区域的软切换，这样在室内外衔接区域以及室内不同定位区域便完成了无缝定位与切换。本算法的结构框图如图1。

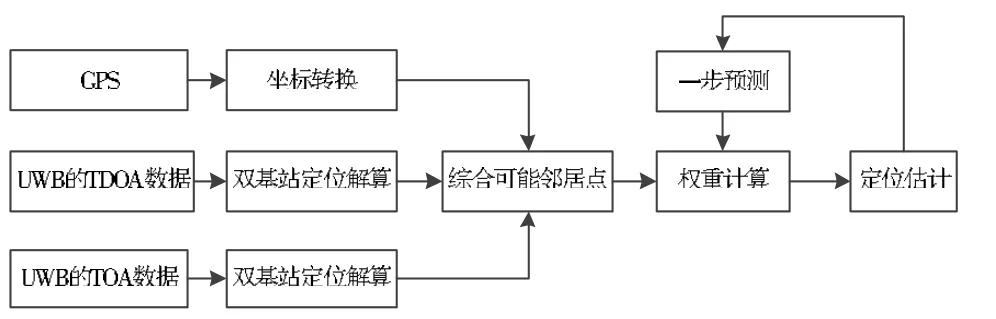
图1 无缝定位算法整体框图

3 室外定位坐标转换

为实现室内UWB和室外GPS定位的数据融合和切换，需把GPS的经纬度数据转换为室内坐标系下的定位数据。为此，可以先选定室外两点，精确测试其GPS位置信息，计算出对应的室内UWB基站点的位置坐标。

此处室外参考点的坐标系是大地坐标系。地面参考点P的位置用大地经度L、大地纬度B和大地高度H表示。采用高斯投影法[4]实现了大地坐标转换为平面坐标(x,y)，变换过程如下：

式中，ΔL为经度差，L为所求点的经度，L0为3度带中央子午线的经度，为椭圆的第二偏心率，B为所求点的纬度；

式中，X为纬度，B为对应的子午线弧长，N为所求点对应的卯酉圈子午线半径。经过上面的计算，便可以把GPS的经纬度信息转换为平面坐标(x,y)的数据[8]。

通过上述的坐标转换便可以把GPS数据转换为当前定位坐标系下的定位近邻点zGPS。

4 室内定位解算

文献[9]中提出了TOA、TDOA的融合算法。本研究提出的融合算法可以融合多种不同测距方式所得的数据，包括TOA、TDOA等。在此仅对基于TOA的定位数据与GPS定位数据进行无缝定位研究，未对TDOA测距数据进行研究与验证。室内定位解算分为两步：双定位基站号序列的确定；双基站定位解算。

4.1 双定位基站号序列的确定

在二维平面中进行定位解算，若使用两个定位基站进行定位，则会出现多解的问题。但在本算法中，使用k最近邻的方法可以通过结合其他双基站的定位信息而使多解问题得到解决，消除定位多解模糊。

进行解算时，首先需要确定两个定位基站。在本算法中，为了更好地利用测距数据，采用定位区域中所有的两个基站组合进行定位解算。另外考虑到现实中UWB测距距离的限制，只考虑基站间距离小于UWB测距距离的基站组合可能情况。以所研究的定位情景图为例，如有效测距最大为D，以区域A中的一个定位实例点M为例，给出在该点M处可进行定位解算的双基站序列如下：

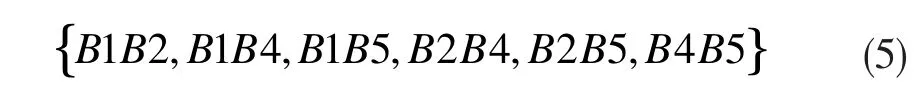
定位实例点M、定位基站位置以及模拟的定位情景如图2所示。

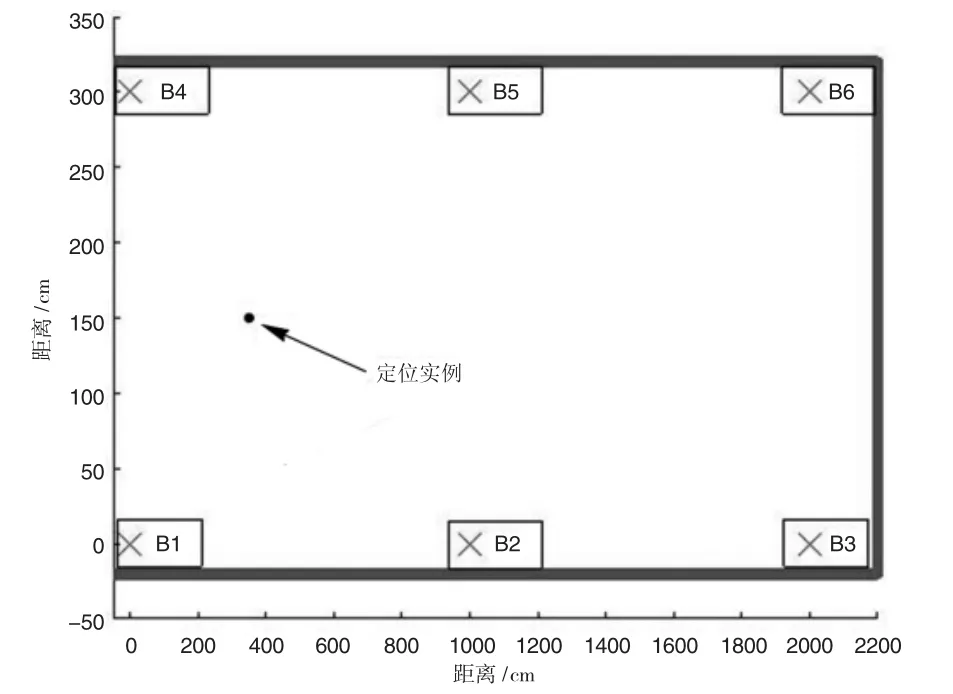
图2 基站位置与定位实例图

4.2 双基站定位解算

在双定位基站确定后，下一步要进行定位的解算。定位解算是基于双基站TOA测距的定位方案，因此定位模型可抽象为两个已知圆求交点的数学模型，如图3所示：

图3 双基站定位示意图

由图3可知，只要知道两个基站的位置坐标(Xa,Ya)、(Xb,Yb),以及基站到标签的距离D1、D2便可进行计算，算出两个圆的两个交点(x1,y1)、(x2,y2)。

每对双基站定位数据可解算出两个定位点，即产生两个定位近邻点，结合上面已给出的双基站序列，通过分别计算不同的双基站序列的定位数据便可计算出该标签在当前环境下所有可能的定位近邻点。这些定位近邻点中包括反映真实位置的点以及多解点，通过下一节将会介绍的k最近邻算法的计算便可从这些定位近邻点中估计出真实的定位点。以下是针对上面给出的定位实例点而产生的定位近邻点的集合：

5 k最近邻计算

通过上面的GPS定位数据的坐标转换和UWB双基站解算，便可得出在该时刻下该标签位置的所有定位近邻点的集合Z。下一步可通过基于变权重的k最近邻算法进行定位点的估计。最近邻的参考位置是由上次估算的目标移动速度和定位估计点进行一步预测而得出的，其计算方法如下：

式中，Si为本次一步预测点，Si-1为上次定位估计点，Vi-1为上次估计的移动速度，T为计算周期。

由k最近邻算法的特点可知，k值的选择非常重要，选得太大会使定位误差增加，而选得太小则可能出现跟踪失败而导致计算发散。在本算法中采用的是动态k的方法，每次计算的k值并不固定。以参考点Si为中心，半径为R的圆内的近邻点的数目即为本次的k值，即ki。因此R的大小决定了ki值可取的大小。在本次研究中暂不对R的选择进行深入探讨，只是取一个比较合理的值。在仿真中，近邻半径R取150 cm。

在近邻数目ki确定后，下一步进行各个近邻点权重大小的计算。在二维平面中，可以由欧氏距离来对距离远近做出评估，因此首先计算出ki个近邻点各自与参考点的欧氏距离，然后利用该距离值来计算在i时刻的第j个近邻的权重wi,j[10]：

式中，f为权重计算函数，(xj,yj)为第j个近邻的坐标值，(x,y)为i时刻的计算参考点。

权重函数有多种，理论上只要与误差成反比即可，如线性函数y=kx+b(k＜0,b＞0)、高斯函数等。在本算法中初步选择均值为0，方差为σ2的高斯函数作为权重函数，且只取自变量在一定范围内的函数值，具体表达式如下：

式中，d为近邻点到参考点的欧氏距离，R为上面提到的近邻半径。L为常数系数，仿真中取值150。权重函数的图形如图4所示。由高斯函数的特点可知，使用高斯函数可以使近邻点的权重分布更集中于参考点附近，而普通的一次函数就没有这个特点。因此选择高斯函数作为权重函数更有利于减小估计的误差，提高估计精度。

在决策阶段，采用的是权重决策机制，即根据不同近邻点的权重进行加权平均进而得出最后的定位估计点如下：

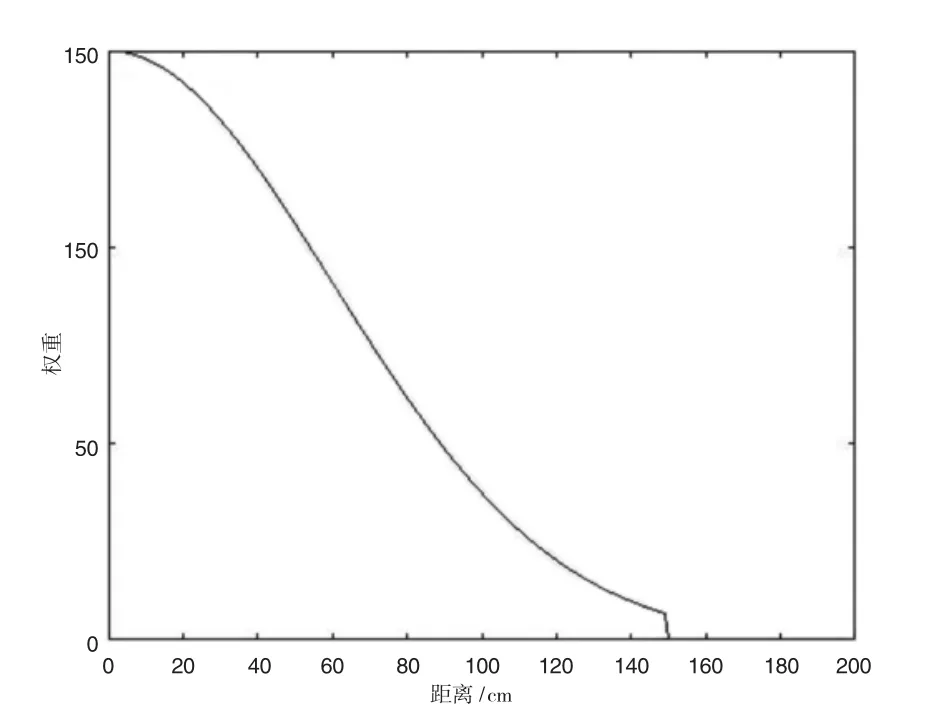
图4 权重函数

式中，wi,j为近邻点的权重，Zi为近邻点的坐标Zi=(xi,yi)T，为近邻个数。

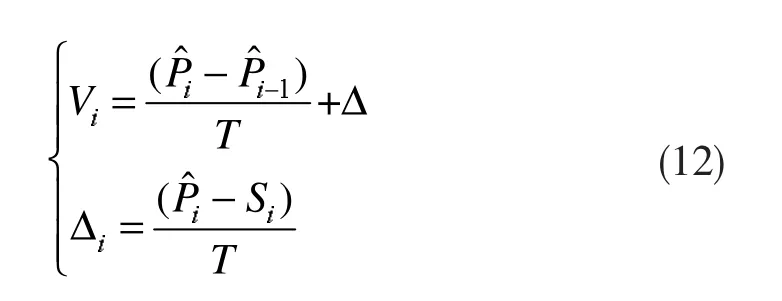
式中，Δ为本次速度估计误差，由本次定位估计点和本次一步预测点的差值决定，Vi为本次的速度估计值。

经过上面的动态权重的k最近邻算法便可估计出本次目标点的坐标Pˆi以及速度 Vi。坐标Pˆi即为最终的定位估计点。

6 模拟仿真与分析

本算法通过模拟现实中的定位场景和定位数据来进行算法验证，采用MATLAB作为仿真平台。定位场景模拟的是室内长廊和室外两个环境，室内长廊分为两个定位区域，其中分布有6个定位基站；长廊右边是室外区域。

为了更好地逼近真实的UWB定位数据，在距离真值的基础上叠加了高斯噪声、随机错误值并通过有效距离函数进行距离的限制。高斯噪声取均值为0，方差为110[11]；随机错误用随机强制置0的方法来模拟UWB出现的定位错误及信号丢失的情况；有效距离函数采用门函数，即：式中，Dmax表示UWB测距的最大距离，di为未进行距离限制的值。

如图5即是仿真实验中目标点到定位基站5的模拟距离数据。

图5 模拟的定位距离数据

通过MATLAB的仿真，得出了定位估计点的轨迹，如图6。由图中可知，定位的估计点和真实的点的偏差非常小，而且在室内不同区域的切换中并没有出现明显的切换间断；在室内与室外的切换区域中，也是平滑过渡的。由于GPS数据的误差更大些，因此在仿真时选取的GPS数据的噪声方差比较大；而UWB测距数据的误差在厘米级[12]。因此在定位轨迹图中会看到在离开室内一段距离（即无UWB测距数据）后，定位的性能明显下降。但和原始的GPS定位点形成的轨迹比较可见，该算法进行定位估计比原始的GPS定位有效果上的提升。

图6 定位估计轨迹

由于初始参考位置点的未知，会出现刚开始时定位估计误差大的情况，因此在刚开始进行估计的几步中（比如图6中为3步），估计位置与实际位置偏差较大，但在收敛到正确值后，估计误差可稳定到很小的正常水平。

由于在本算法中会用到速度来对定位估计进行一步预测作为k最近邻的参考点，因此速度的估计也直接关系到定位的精度；而且在实际的定位应用中，也希望得到目标移动速度的估计。在仿真中给定的是匀速运动，对目标速度估计的曲线如图7。

图7 目标速度估计

由速度估计的数据可知，在刚开始估计时由于定位估计初始点的未知而未收敛到正确值，因此其估计误差比较大；在经过几步计算后，估计值已收敛到正确值附近，而且收敛的速度也比较快。在图7中可观察到，估计计算在4步之后已经收敛。

为了定量地分析定位误差，计算了在定位过程中各定位估计点与真值的偏差，如图8。

图8 定位偏差图

通过定位误差图可明显看出本算法定位估计的性能。在刚开始，会由于初始参考点的未知而造成定位估计的误差较大，但经过很短的几步计算后便趋于稳定，稳定在误差小于10 cm的范围内。在图8中已标出区域切换的位置（室内区域切换和室内到室外的切换），可以看出，在这两个位置附近的定位误差并没有出现明显的突变，因此证明了该算法完成了不同区域软切换的目标；由于在室外环境中GPS数据的误差要大于UWB的测距误差，因此在定位的后半段，估计的误差会逐渐变大，直到UWB数据完全失效后，定位误差稳定到一个比较固定的数值。

为了显示在不同位置处产生定位近邻点的情况，选取了四个比较典型的位置进行定位近邻点的显示，如图9。

图9 定位近邻的分布图

从图中可以看到，在不同的定位位置计算出的定位近邻数是不同的：在图9(a)中，由于只能接受到4个基站的定位数据，因此计算出的定位近邻数最多为6；在图9(b)中，接收到两个定位区域的6个基站的测距数据，因此计算出的定位近邻数最多为11；在图9(c)中，该位置是处在室外区域，为定位过渡带，只能接收到2个定位基站的数据和1个GPS的数据，因此最多会产生2个定位近邻；在图9(d)中，由于UWB定位已失效，只有GPS的数据，因此定位近邻只有一个GPS的数据。

从图9(c)中还可看出，即使只有两个定位基站的测距数据也可以进行正常的定位，而在其他的算法中，这一点是做不到的。该算法可以在只有两个基站数据的情况下进行正确定位，其原理在于每次进行一步预测的k最近邻的参考点是由历史数据估计出来的，该数据提供了消除多解的方向信息，因此在只有两个基站的两个定位解中，会选择离该参考点最近的点作为估计，从而消除定位模糊。本算法的该项特点也使得在定位环境恶劣的情况下不会出现定位错误甚至无法定位的问题，增加了定位系统的鲁棒性。

7 结束语

此种基于变权重k最近邻算法的室内外无缝定位算法，融合了多种定位信息的方法，不但解决了室内外定位无缝切换的需求，而且也克服了室内的不同定位区域切换不流畅的问题；在定位精度方面，由于采用多个定位基站以不同排列组合进行定位，充分利用了不同方位基站的定位信息，使定位精度进一步提高，抑制了非视距传播的影响。而且由于该算法的权值调整作用，使定位数据实现了滤波的效果，使定位数据更平滑。该算法采用迭代计算的方式，大大提高了运算速度，可以应用于实际中高刷新率的定位服务中。

由于本研究中并没有对基于TDOA的UWB数据加入到融合算法进行研究，只是提出了这样一个融合框架，因此接下来要加入基于TDOA的UWB数据进行研究。而且在由历史数据进行一步预测的方法也存在可改进的空间。后续工作重点将围绕这两个方面展开，进一步提高该无缝定位算法的性能。