基于GIS技术的高校内建筑火灾人员疏散模型研究*

杜微微，张玉红

（哈尔滨师范大学地理科学学院，哈尔滨150025）

1 引言

近年来，校园火灾频发，校园的消防安全也逐渐引起高校管理者的重视，促使了人力、物力投入的加大，也取得了一定的成果。但是，在高校大幅度扩招和后勤市场化改革之后，新时期的高校校园消防安全管理也面临着新的挑战。尤其是，国内很多高校的校园建筑是上世纪的老旧建筑，电气设备老化，耐火性能差，消防设施陈旧，建筑复杂度高；与此同时，在教育改革及科技进步的背景下，电脑、手机的应用越来越广泛，校园建筑物内的电路负载不断加大，校园安全隐患也日益突出。近期，国内多所高校接连有火灾发生，导致了重大的生命和财产损失。高校建筑内部人员密度大，而且存在大量易燃装饰物、木质课桌等，很容易导致火灾并随之产生烟雾的蔓延。为此，在高校建筑火灾发生后，必须考虑逃生线路上所存在的火灾和烟雾危险，以及线路上的人员拥塞情况，设法实现疏散方案的动态调整，以保障火灾发生时高校建筑内人员的顺利逃生和获救。

故此，本研究基于GIS技术，在空间、时间两个维度上对高校建筑物内的火灾发生过程进行模拟，制定有针对性的高校建筑内火灾灾情快速评估及人员疏散方案，以辅助高校建筑内部火灾灾害的预防与减灾。

2 火灾场景空间模型构建

2.1 火灾场景几何分解

高校建筑火灾救援中的几何模型是指建立起与高校建筑真实布局与计算机模型之间的对应关系，使用计算机语言进行高校建筑布局特征的描述。在使用GIS技术进行高校建筑内几何场景进行分解时，首先需要通过高校内建筑几何模型的分解，实现高校建筑连续几何空间的离散化描述，使用图论等理论进行数据结构的设计，是火灾疏散模型研究的基础。当前常见的建筑内部场景解析方案如图1所示。

图1 高校内建筑几何模型解析

计算几何模型分为粗细两种类型的网络模型。在粗网络模型中，将高校建筑物内的房间作为图中的节点，这些节点的连接通道作为图中的弧段。这种方式在于计算简单，可在宏观上把控疏散特征，其缺点在于过于抽象，难以对高校建筑内人员轨迹进行精确跟踪。细网络模型采用圆形、六边形或矩形等形式对建筑空间进行更加细致的划分，划分的粒度保证每个节点无法被两个以上的人同时占据。由于高校建筑物内的人员数量较多，若几何节点过于抽象，难以实现人员轨迹的精确跟踪，为此在本模型中，使用细网模型进行火灾场景解析。

2.2 空间模型节点描述

合理的数学结构设计，有利于计算机存储空间的优化，和有利于提高程序的运行效率。由于所采用的建筑内空间的网状几何模型的数据量大，节点间的联系非常灵活。因此，针对建筑空间的网状几何模型的数据结构设计尤为重要。通过对图形结构特征的分析可以看出，节点应具备一定的可扩展性，以适应不同情形的属性。为此，选用如下的结构体，对图形节点进行描述：

其中，no中保存集结点编号，DATA为用户自定义数据类型，例如表示建筑物内某个具体房间内空间节点的空间坐标、节点类型、节点半径、此时是否有人占据该节点的标志等。

对于网络中的弧而言，考虑到弧的弧长和权值等因素，也需要将图形结构中的数据结构设计为可扩展形式，与网络模型中的节点类似，利用EDEG结构体存储网络中的弧信息：

其中ori_no变量存储网络中的弧起始节点编号；dest_no存储网络中的弧终端节点编号；data变量存储边的描述信息。

在网状几何模型的存储过程中，除了需要对网络的点和弧信息进行存储以外，还需要对节点间的组织连接方式进行设计。当前常见的网络节点存储方式包括邻接矩阵、邻接表和邻接多重表等方式。如果图中的弧数量远少于节点数量时，使用邻接矩阵的方式存储网络节点，将会导致大量零元素的存在，导致存储空间的浪费。邻接表可节省存储空间，而且与邻接多重表相比，其结构更加简单，查询和便利功能也更加易于实现，也更加符合常规思维方式。为此，本模型选用邻接表数据结构对网络节点及其连接方式进行存储。

邻接表的核心就是针对网路中的每个节点建立链表，链表中存储了节点间的弧信息。网络的邻接表数据结构的具体描述如图2所示。

图2 网络的邻接表数据结构形式

图2的左边为网络的具体形式，右边为相应图形的链表结构表现形式。采用如图2所示的数据结构即可对建筑物内的几何模型节点进行描述。?

2.3 基于GIS技术的火灾场景空间解析

如上所示，通过计算集合模型的设计和存储数据结构的存储，可以根据高校建筑物内的几何信息，生成由众多节点所构成的图结构，其中每个节点具有一定的面积，而且在火灾救援过程模拟时，可以被且仅被1个人所占据。人员可以通过节点间的连接弧，实现节点间的移动。对于高校内不同建筑物的布局，每个节点可以是出口、梯段等不同类型的节点，每条弧都有长度等扩展属性。图形结构不仅可以用于建筑内集合空间拓扑关系的描述，同时也存储了高校建筑物内空间布局的相关信息。

针对建筑物内空间平面的具体布局情况，可以使用GIS技术自动生成对应的计算机图结构。每个高校建筑内平面空间可被看作一系列计算机图结构的集合。用GIS文件实现对图形的访问。

使用GIS技术对建筑平面空间信息进行解析的算法设计如下：

①指定建筑内平面空间的任意节点P0，将P0节点加入到节点列表中；

②以P0节点为起点，按照顺时针方向进行搜索，如果未遇到障碍物，则建立新节点，并将节点加入到节点列表中，同时根据搜索情况，在计算机图形结构中加入相应的弧信息，如果在该搜索方向上已经存在节点，或无足够有效空间，则执行下一个搜索方向，若该节点的所有方向搜索完毕，则跳转到对下一个节点进行处理；

③遍历所有节点列表，直到数据结构中的节点均处理完毕为止，至此完成整个建筑几何空间的搜索建模。

上述过程整体描述如图3所示。

图3 建筑几何平面节点解析过程

在得到GIS技术解析后，最终的建筑几何平面结构如图4所示。

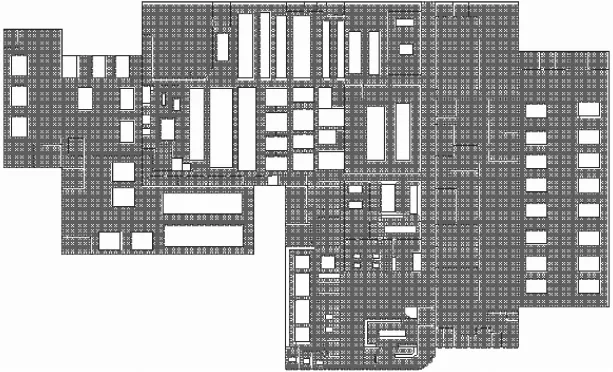
图4 基于GIS技术解析的建筑几何平面结构图

3 建筑火灾人员疏散模型构建

在完成建筑几何平面的网状结构划分后，结合图结构计算模型，可采用Bellman-Ford-Moore算法、Dijkstra算法和A*算法等方式对建筑内人员疏散路径进行分析，进而生成建筑火灾人员疏散模型。同时，由于建筑内人员疏散过程的复杂性，简单的疏散路径分析方法无法充分体现高校建筑内火灾发生后建筑内人员的真实疏散情形。为此，需要不断进行规则的修改、完善和增强，不断健全建筑内人员疏散过程的推理机制。

3.1 疏散线路选择

在上述疏散路径生成算法中，Bellman-Ford-Moore算法是公认最好的赋权路径算法，但是其计算量较大，收敛速度偏低；Dijkstra算法起点为中心，不断线网扩展，直到扩展到终点几点为止，该算法需要计算的节点较多，效率偏低，不适合高校大型建筑节点数量众多的场合；A*算法属于最好优先的启发式图搜索算法，利用启发信息以提高路径搜索效率。在运用A*算法进行疏散路线搜索时，将已经计算得到的线路长度进行存储，并根据长度对疏散路线进行排序，实现线路长短比较。由于建筑内疏散路线的可选择性较多，本模型中使用快速排序算法，以保证疏散路线选择的性能。

在确定可达的疏散路径后，在GIS空间中，按照可达的疏散路线生成平行带状多边形缓冲区。分析缓冲区内的烟气、火势分布情况，并判断该可达疏散路线的危险性，以及线路上的人员拥挤程度，以规避高风险和拥塞的疏散线路。

3.2 疏散策略调整

通过上述分析，基于对疏散路径的可达性、危险性和拥塞程度的了解，就可对已有的疏散策略进行调整，选择其他可达的、危险性低和拥塞程度低的疏散路径，确保能够及时从火灾建筑中撤离。

疏散策略调整的量化判断条件如下式所示：

其中，flow_rate为建筑内的人群整体移动速度，取值[0.1,0.3]区间。若该疏散路径具有较高的危险度或拥塞度，则下式成立：

其中，FireNodes、SmokeNodes、PeopleNodes分别表示疏散路径上的着火节点、烟气覆盖节点和人员占领节点。通过如上疏散路径判别公式的设计，使得高校建筑火灾救援中的行为更加真实，也可以科学合理地指导建筑内人员的逃生。

在本模型的研究中，在图结构计算模型基础上，主要利用A*算法，求解两点间的最短路径，其具体实现结果如图5所示。

图5 A*算法的最短路径搜索结果

通过对建筑内几何平面关键点的A*算法最短路径的结合，并且根据疏散策略调整结果，最终形成如图6所示的建筑火灾人员疏散模型，以指导高校建筑火灾发生时建筑内人员的逃生。

图6 建筑火灾人员疏散模型

4 结束语

火灾是危害社会公众安全的主要灾害之一，建筑火灾中的建筑空间布局、电能失效、浓烟、人员动态等因素影响着人们快速撤离火场的效率。所提出的建筑火灾人员快速疏散模型可真实体现高校建筑内火灾发生后建筑内人员的真实疏散情形，有助于不断健全建筑内人员疏散过程的推理机制，确保在火灾中及时安全撤离，将损失降至最低。