面向模型未知的自由漂浮空间机械臂自适应神经鲁棒控制

王 超,蒋理剑,叶晓平,蒋黎红,张文辉

(丽水学院 工学院,浙江 丽水 323000)

空间机械臂在空间技术发展中扮演着越来越重要的角色.由于太空燃料极其宝贵,为延长飞行器的使用寿命,研究基体位置与姿态均不受控的自由漂浮空间机械臂更具价值[1-2].自由漂浮空间机械臂自身运动必然引起基座耦合运动,系统非线性更强,且由于载荷变化、外界干扰、参数摄动等不确定性因素,空间机械臂精确数学模型也难以获得,这对高精度控制提出了挑战[3-4].

针对载体位置、姿态均不受控的自由漂浮空间机械臂稳定控制问题,文献[5]较早提出了基于神经网络的自适应控制方法,并将其应用于自由漂浮空间机械臂.文献[6]针对存在摩擦死区非线性的空间机械臂系统,提出了基于神经网络的补偿控制策略.文献[7]针对空间机械臂模型的未知不确定问题,提出了基于神经网络的自适应控制方法.文献[8]针对关节空间下的机器人轨迹跟踪问题,提出了基于确定学习理论的模式控制策略.文献[9]面向非合作目标空间机械臂载荷捕获问题,研究了一种末端质量突变的神经变结构冗余控制方法.

针对参数不确定性及外界干扰等不确定问题,提出一种面向模型未知的自适应神经网络鲁棒控制方法.建立漂浮基空间机器人动力学模型,设计基于精确模型的线性PID控制器;提出神经网络控制方法来逼近未知模型,设计网络权值的自适应学习律来实现在线实时调整,避免对数学模型的依赖;设计自适应鲁棒控制器来抑制外界扰动和补偿逼近误差,提高鲁棒性和控制精度;基于Lyapunov理论,证明了闭环系统的稳定性.仿真试验验证了所提控制方法的有效性.

1 自由漂浮空间机械臂动力学方程

在空间机械臂基座位置及姿态均不受控制的模式下,系统遵守动量守恒和动量矩守恒,由于太空失重环境,忽略微弱重力势能,此时拉格朗日算子等于系统动能,基于第二类拉格朗日法可推得n关节空间机械臂全驱动形式动力学方程[4-9]为

(1)

空间机械臂动力学方程(1)性质如下[4-8]:

性质1M(qb,qm)为对称正定矩阵.

2 线性PID控制器设计

漂浮空间机械臂动力学方程可转化为

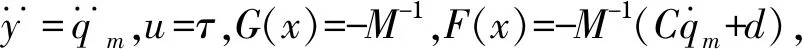
(4)

定义期望轨迹为

定义轨迹跟踪误差为

(5)

定义滤波跟踪误差函数为

(6)

由式(6)知,若si→0,则ei→0(i=1,2,…,p).

根据牛顿二项式定理,将式(6)代入式(5),得

(7)

则

其中,

⋮

(10)

有

令

则式(9)可写为

(11)

如果M,C和d能够精确获得,非线性函数F(x)和G(x)已知,则设计线性PID控制律如下:

(12)

式中:K0=diag[k01,k02, …,k0p],k0i>0,i=1,2，…,p.

3 自适应神经网络鲁棒控制器设计

实际系统中,由于参数不确定及外界干扰等因素,非线性函数fi(x)和gij(x)无法精确获得,考虑到神经网络优越的非线性逼近能力,设计神经网络控制器来逼近fi(x)和gij(x).

其各自的RBFNN最优输出为

根据RBF神经网络的逼近能力,假设[6-9]:

(17)

(18)

(19)

(20)

(21)

式中:ε0为任意小的正整数;Ip为单位阵.

为消除神经网络的逼近误差及外界干扰,提高控制精度,设计鲁棒控制器ur,则

(22)

(23)

式中:Ks为一个正常数;δ为变量.

则自适应神经网络鲁棒控制器设计为

(24)

自适应控制律为

式中:ηfi>0;ηgij>0;η0>0;δ(0)>0.

定理1自由漂浮空间机械臂动力学方程式(1)在满足假设条件时,采用控制律式(21)～式(24)以及自适应律式(25)～式(27),可保证系统闭环系统的所有信号有界,且轨迹跟踪误差及其各阶导数一致收敛于零.

证明将式(24)代入式(11)可得

(28)

由于

(29)

则由式(21)和式(29)得

(30)

将式(30)代入式(28)得

(31)

对式(31)两边分别乘以sT,有

(32)

定义Lyapunov函数

(33)

则

(34)

将式(32)代入式(34),得

(35)

其中,

(36)

(37)

将式(25)和式(26)代入式(36),得

(38)

由式(37)得

(39)

将式(38)代入式(39),得

(40)

将(27)代入式(40),得

从而

(41)

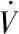
对式(41)积分

4 算法验证与分析

以双关节漂浮基空间机械臂为例进行控制系统分析,具体参数及其物理意义同文献[9].假设扰动误差为

期望的轨迹为

神经网络初始权值为0,各基函数宽度及中心在输入输出域中随机选取,隐层节点数40.

方法1为线性PID控制器,方法2为自适应神经网络鲁棒控制器.仿真试验结果如图1～图4所示.

由图1可以看出方法1能够保证控制系统稳定性;由图2可以看出方法1的控制力矩也不大,但是存在较大稳态误差,说明单纯的线性控制无法实现对耦合非线性系统的精确控制.

由图3可以看出采用方法2后,系统在大约1.5 s内达到较好完全跟踪期望轨迹,且控制精度较高.由图4可以看出方法2的输出力矩也相对较小,且力矩输出比较稳定.由于鲁棒控制器中增益作用,因此力矩存在微小方波波动,能够较好抑制外界干扰.

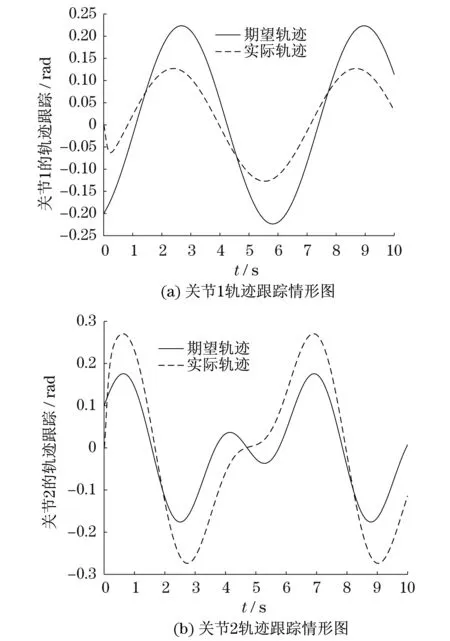
图1 方法1轨迹跟踪控制图Fig.1 Trajectory tracking graph of method 1

图2 方法1控制力矩图Fig.2 Control torque diagram of method 1

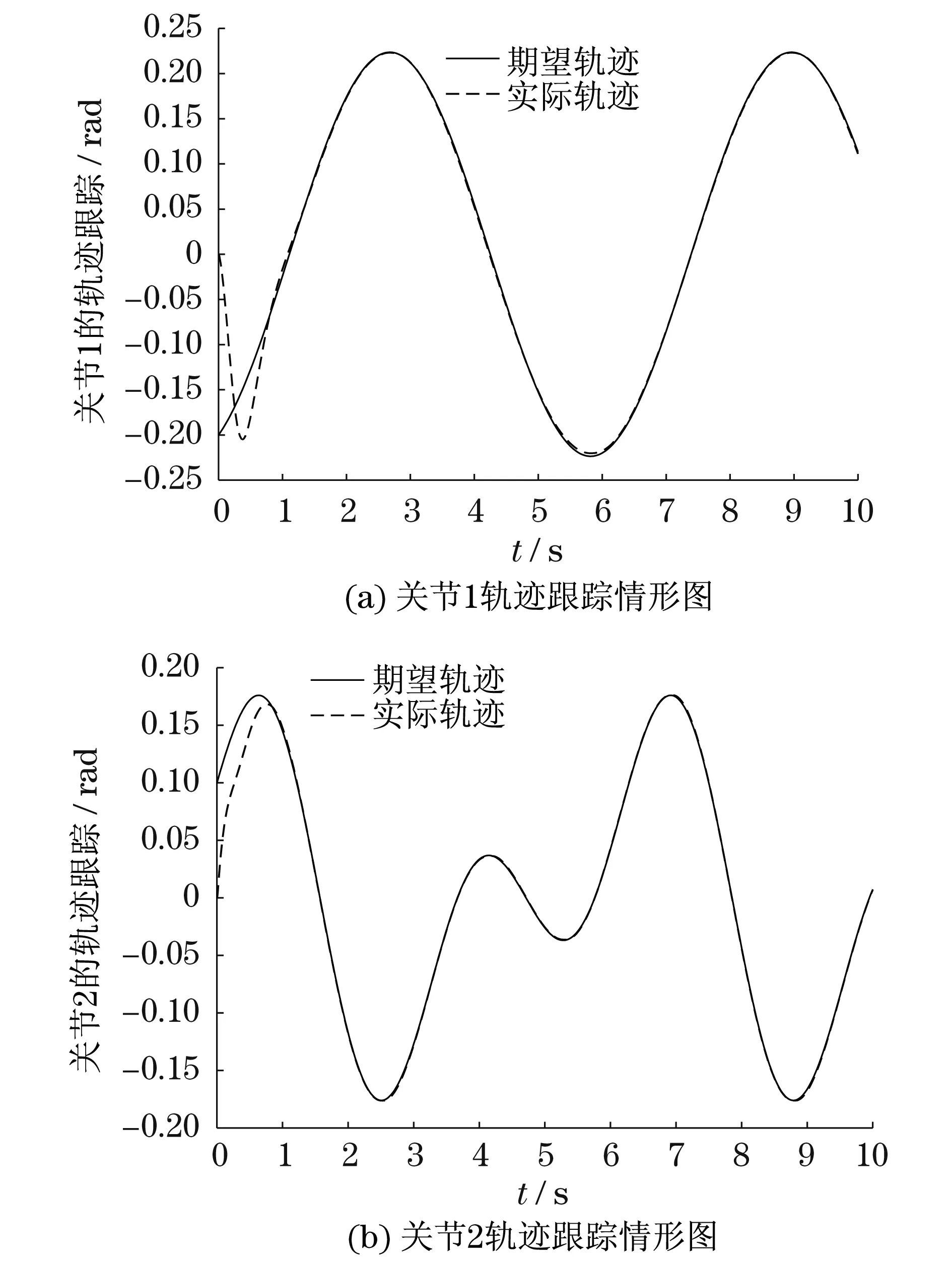
图3 自适应神经鲁棒控制器的轨迹跟踪图Fig.3 Trajectory tracking graph of adaptiveneural network robust controller

图4 自适应神经鲁棒控制器的力矩图Fig.4 Torque diagram of adaptive neuralnetwork robust controller

5 结论

针对精确模型未知及存在外界干扰的自由漂浮空间机械臂控制问题,提出了一种无须模型的自适应神经网络鲁棒控制方法.首先建立漂浮基空间机械臂动力学模型,设计了基于精确模型的线性PID控制器,并证明了系统稳定性;采用神经网络控制器来逼近未知模型,并设计了网络权值的自适应学习律,实现在线实时调整,避免了对空间机械臂精确数学模型的依赖;针对外界扰动和逼近误差,设计了自适应鲁棒控制器,提高了系统鲁棒性;基于Lyapunov理论,证明了闭环系统的稳定性.仿真试验验证了所提控制方法的有效性,对于类似非线性系统研究具有重要价值.