分段刚度双质量飞轮非线性振动特性研究*
史文库,陈 龙,陈志勇,丁 吉
(吉林大学,汽车仿真与控制国家重点实验室,长春 130022)
前言
双质量飞轮能够有效衰减汽车传动系扭转振动,自20世纪80年代LUK公司首次提出后,得到汽车公司广泛应用,大有取代离合器扭振减振器之势[1-4]。但是由于汽车行驶工况复杂,依靠单级线性刚度双质量飞轮已经无法满足车辆全部行驶工况的减振降噪需求,因此多级非线性刚度双质量飞轮成为了研究热点。由于国外在双质量飞轮的研发较早,多级非线性双质量飞轮已经形成了性能稳定的产品,其中以LUK公司为代表的双质量飞轮生产商在2015年其生产总量累计已经超过1亿个,而国内还处于研发初期。吕振华等[5-6]针对不同结构形式弹簧的双质量飞轮的多级非线性弹性特性进行研究;史文库等[7-8]针对多级刚度双质量飞轮的设计方法进行研究,并对其减振效果进行仿真分析与优化;江征风等[9-10]针对多级刚度双质量飞轮的设计方法进行研究;宋立权等[11-12]提出一种摩擦式双级分段变刚度轴向短轻直弹簧式双质量飞轮。
本文中以两级分段线刚度周向长弧形双质量飞轮为研究对象,利用平均法研究分段线刚度的双质量飞轮在扭转振动过程中的非线性振动特性。该方法可扩展到三级线刚度或者其它形式的非线性扭转刚度双质量飞轮非线性振动特性研究中去,为非线性双质量飞轮的设计开发提供参考。
1 双质量飞轮分段非线性动力学模型
周向长弧形双质量飞轮的结构如图1所示。它是由第一质量飞轮、第二质量飞轮、传力板和长弧形弹簧等部件构成。由于双质量飞轮第一质量与第二质量通过低刚度弧形弹簧相连接,从而将传动系统的共振转速降低到怠速转速以下。但是单级扭转刚度的双质量飞轮无法为汽车全部行驶工况提供良好的减振性能,不能同时满足汽车复杂的减振性能和缓冲性能要求[13]。为进一步提升双质量飞轮的扭转减振性能,满足汽车不同工况时不同的扭转刚度需求,多级非线性双质量飞轮便应用而生。
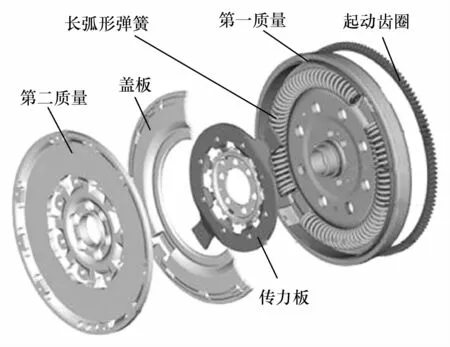
图1 周向长弧形双质量飞轮结构图
1.1 两级分段弹簧工作原理
两级分段弧形弹簧结构是由刚度较小的外弧形弹簧(角刚度为k1)和刚度较大的内弧形弹簧(角刚度为k2)内外嵌套组合而成。两级分段弧形弹簧的结构如图2所示[14]。内弧形弹簧嵌套在外弧形弹簧里。弹簧自由状态时,内、外弧形弹簧分布间隙为 θ0。
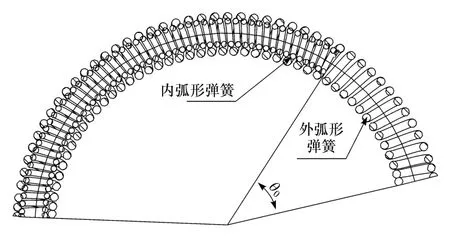
图2 两级扭转刚度弧形弹簧结构
(1)当发动机工作在怠速或者小负荷运行工况下,此时外弧形弹簧压缩变形量小于θ0时,此时双质量飞轮仅有外弧形弹簧参与工作,其第1级刚度为 K=k1;
(2)当发动机工作在大负荷运行工况下,此时外弧形弹簧压缩变形量大于θ0时,此时双质量飞轮内、外弧形弹簧并联参与工作,其第2级刚度为K=k1+k2。
综上所述,可得到双质量飞轮两级分段刚度的非线性弹性模型。
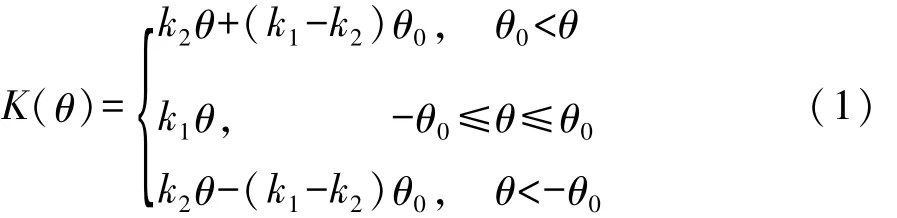
式中:θ为双质量飞轮相对扭转角度;K(θ)为非线性扭转弹性力函数。可见当|θ|>θ0时,内弧形弹簧开始接触并参加工作使刚度增加,得到较大的刚度特性。两级分段扭转刚度特性曲线如图3所示。
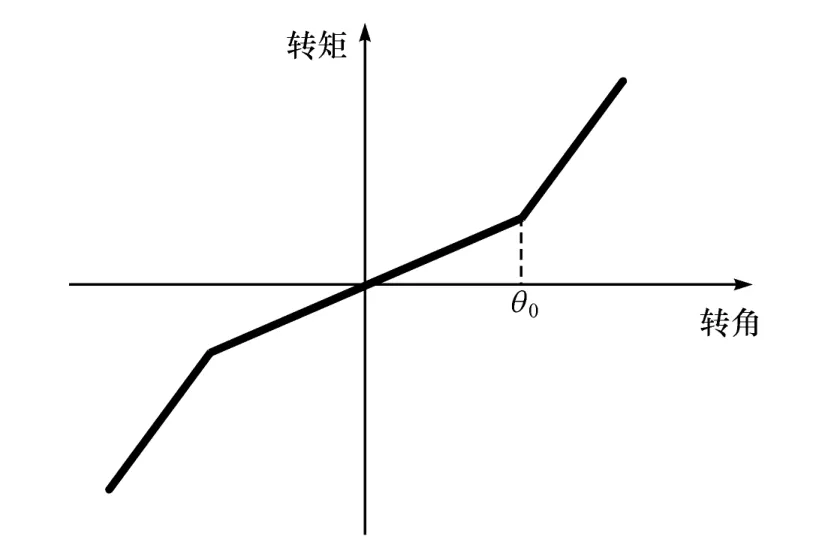
图3 两级分段扭转刚度特性曲线
1.2 非线性双质量飞轮动力学模型
双质量飞轮第一质量转动惯量设为J1,第二质量转动惯量设为J2,第一、第二质量转动惯量的角位移分别设为θ1和θ2,双质量飞轮的扭转刚度和扭转阻尼分别设为K和c,双质量飞轮简化模型如图4所示。
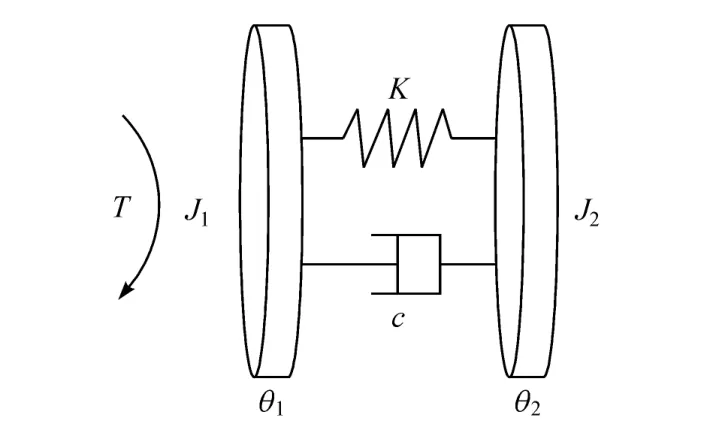
图4 双质量飞轮简化模型
根据双质量飞轮简化模型可得到双质量飞轮非线性振动方程:
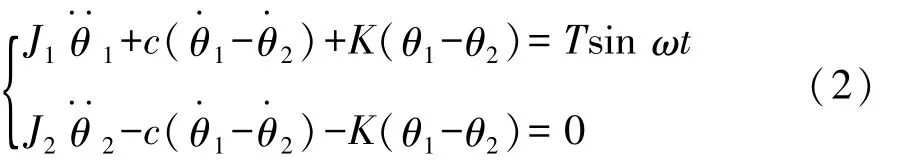
由于双质量飞轮第一质量是与曲轴刚性连接,且双质量飞轮主要目的是降低第二质量扭转振动,在第一质量输入激励固定时,相对转角也可以反映第二质量的波动程度。所以在对双质量飞轮进行动力学分析的过程中,为便于分析计算,将式(2)转换为

2 非线性动力学方程求解
将系统方程转化为拟线性方程[15-17],并将阻尼、弹性力非线性部分等比较小的项前标以小参数ε,可得

式中:a1=k1/J;a2=k2/J。式(6)为具有分段非线性特性的双质量飞轮动力学方程。
假设系统一次近似解形式为

式中a,φ都是关于t的函数。根据平均法,可将式(7)转化为振幅和相位为未知量的标准方程:
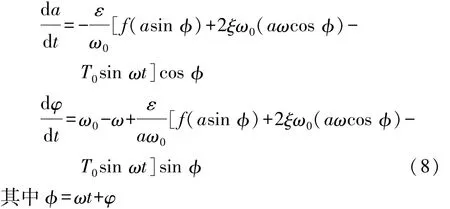
从式(8)可以看出a,φ的导数与ε成比例,故它们为缓慢变化的函数,采用第一次近似的KB(克雷洛夫 包戈留包夫)[18]变换:

式中:Y1,Z1不显含 t;U1,V1,Y*,Z*为 ϑ的以 2π为周期的周期函数,以及t的周期函数。
将式(8)代入式(7),并考虑式(9),可得

令上式两端ε的一次项系数相等,则可得到确定 Y1,Z1,U1和 V1的微分方程。

为求出上式积分,将θ代入式(7)中,并给出相应的积分界限:

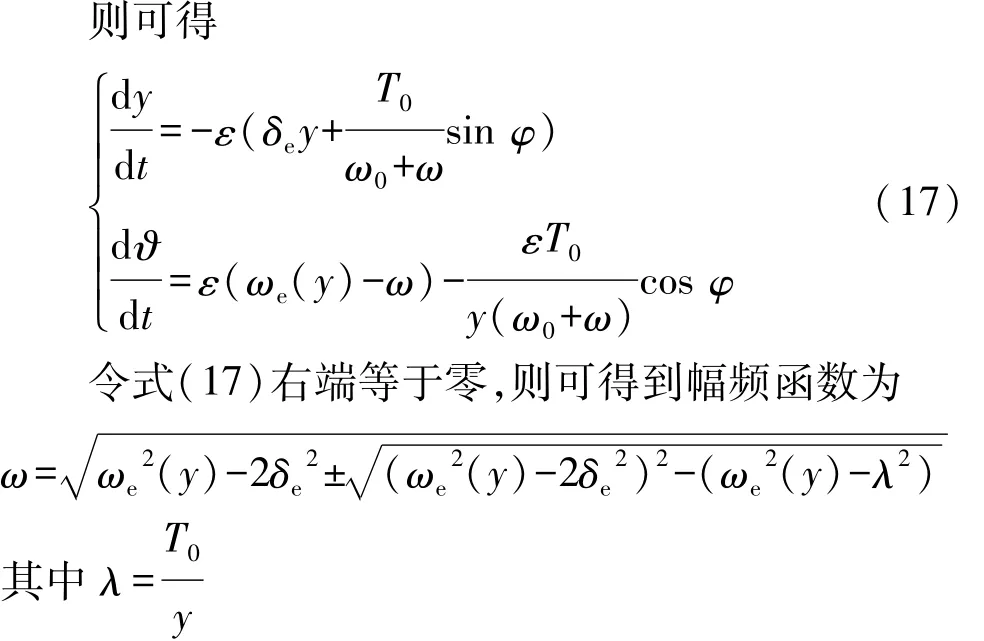
3 非线性振动特性分析
所分析的双质量飞轮基本参数如下:第一质量转动惯量J1=0.2709 kg·m2,第二质量转动惯量J2=0.1355 kg·m2,第一级扭转刚度 k1=8.03 N·m/(°),第二级扭转刚度 k2=18.4 N·m/(°),阻尼系数c=0.1 N·m·s/(°),分布间隙 θ0=32°,激励幅值为60 N·m。
根据幅频函数可得幅频特性曲线,如图5所示。可以看出,在两级弹簧非线性弹性力的作用下,骨干曲线会在θ0=32°处出现拐点,频率响应曲线整体向右拐弯。
在激励幅值一定的前提下,随着激励频率从低频到高频的缓慢增加,系统响应振幅会沿着曲线AB-C增加并一直到达峰值C点;若激励频率继续增加,振幅会突然从C点跳至频响曲线响应值较低的E点上,然后随着激励频率继续增加从E点沿频响曲线逐渐下降。
如果激励频率是从高频到低频逐渐减小,则响应振幅沿频响曲线逐渐增加至点D,此时激励频率继续减小的话,则会从D点突然跳跃到B点,在沿着B-A逐渐减小。
从上面的分析可得在整个过程中,会出现跳跃和滞后现象,而这些过程会导致系统的不稳定。
3.1 激励幅值对幅频特性的影响
当激励幅值分别为25,60和95 N·m,根据幅频响应函数可得到不同激励幅值下的幅频特性曲线,如图6所示。随着激励幅值的增加,骨干曲线没有变化,但是双质量飞轮会在更早的频率下出现非线性特性,同时系统的共振频带变宽,共振峰值变大。当激励幅值较小,系统响应峰值未达到两级刚度的拐点,系统表现为线性系统。激励幅值较大时,系统跳跃幅值也会加大,降低弧形弹簧使用寿命。
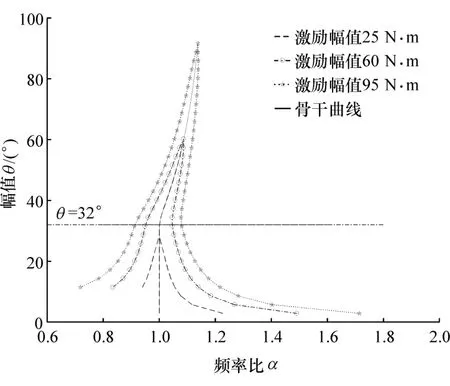
图6 不同激励幅值下的幅频特性曲线
3.2 分布间隙对幅频特性的影响
不同双质量飞轮两级刚度分布间隙θ0的幅频特性曲线如图7所示。通过图7可以发现,不同的分布间隙对系统的振动特性有着非常大的影响。分布间隙越小,双质量飞轮幅频特性曲线的拐点发生的频率也越低,容易激起非线性振动;分布间隙越小,共振曲线的非线性特性越发明显,同时共振峰值也有降低的趋势。
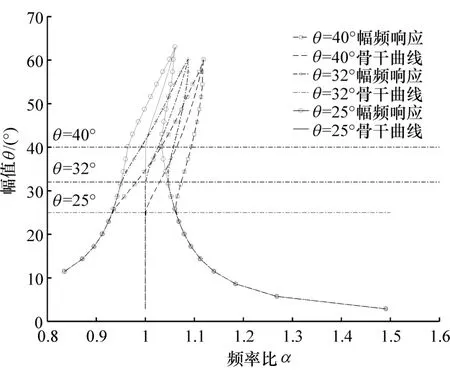
图7 不同分布间隙下的幅频特性曲线
3.3 扭转刚度对幅频特性的影响
分别对双质量飞轮两级刚度取其80%,100%和120%,并得到其幅频特性曲线,如图8所示。第1级角刚度k1和第2级角刚度k2的增加都会导致幅频特性曲线加剧向右拐;但是第1级刚度k1的增加会导致共振频带变宽,同时共振幅值增大,而第2级刚度k2的增加则对共振频带影响不大,同时可以降低共振峰值。
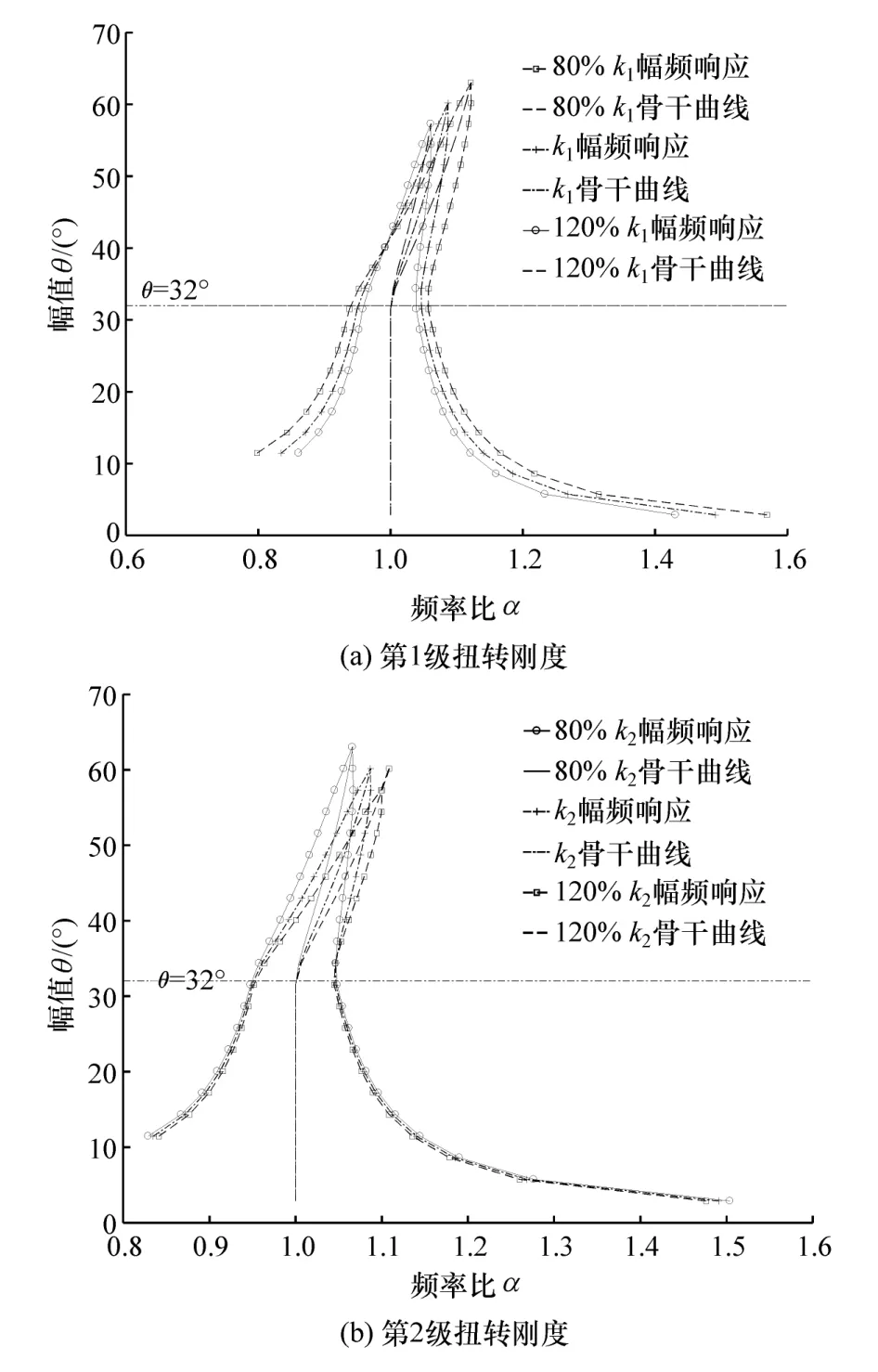
图8 不同扭转刚度下的幅频特性曲线
3.4 阻尼对幅频特性的影响
改变双质量飞轮的阻尼系数,分别取c=0.05,c=0.1和 c=0.2 N·m·s/(°),得到不同阻尼系数下的幅频特性曲线,如图9所示。可以发现,随着阻尼系数的增加,共振峰值大幅度减小,同时高频区域阻尼大小对系统响应幅值影响不大。因此,适当的增加阻尼可有效抑制系统共振峰值。
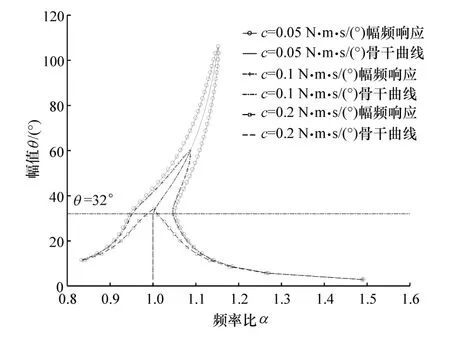
图9 不同阻尼下的幅频特性曲线
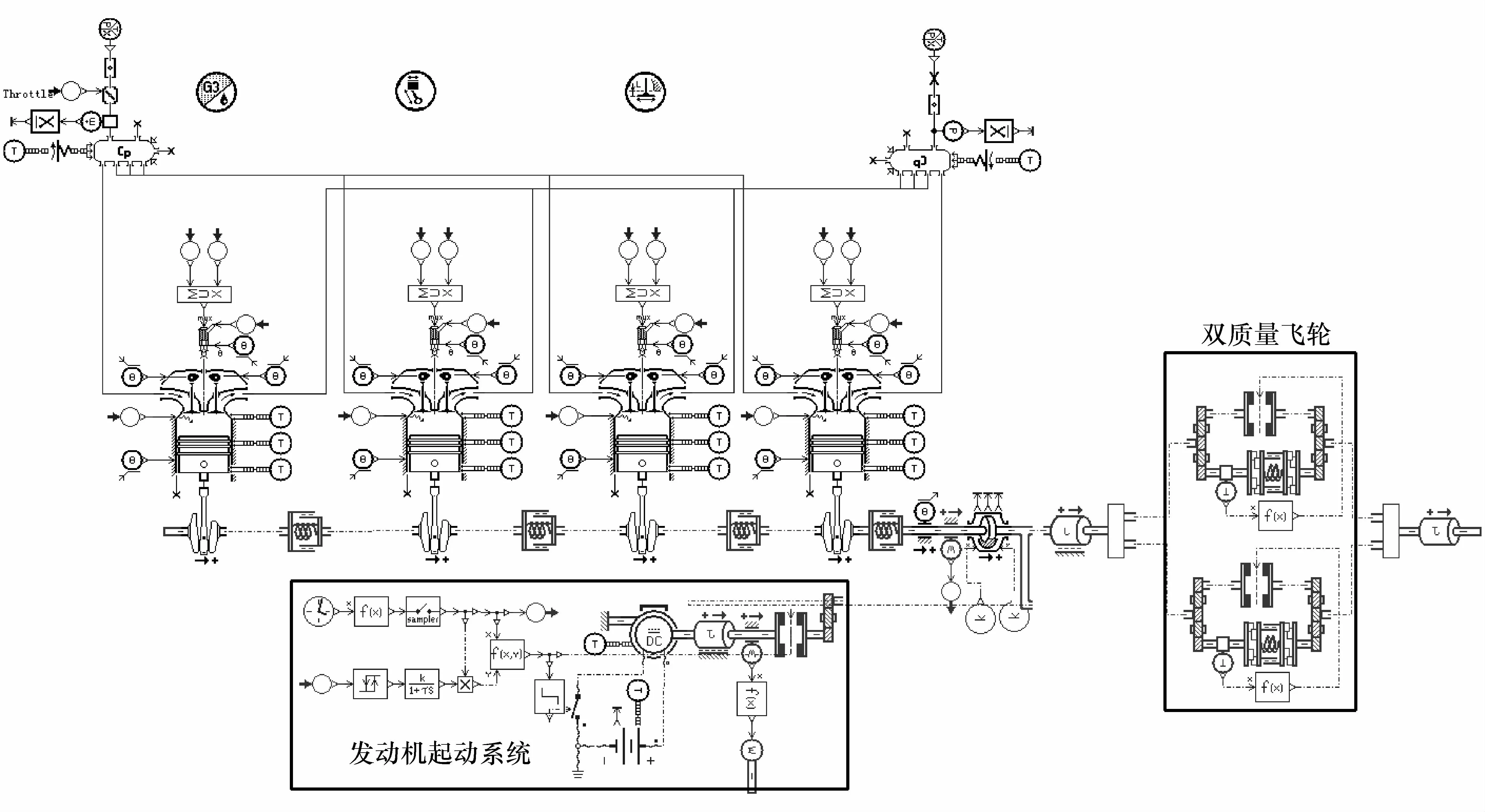
图10 AMEsim点火、熄火工况仿真模型
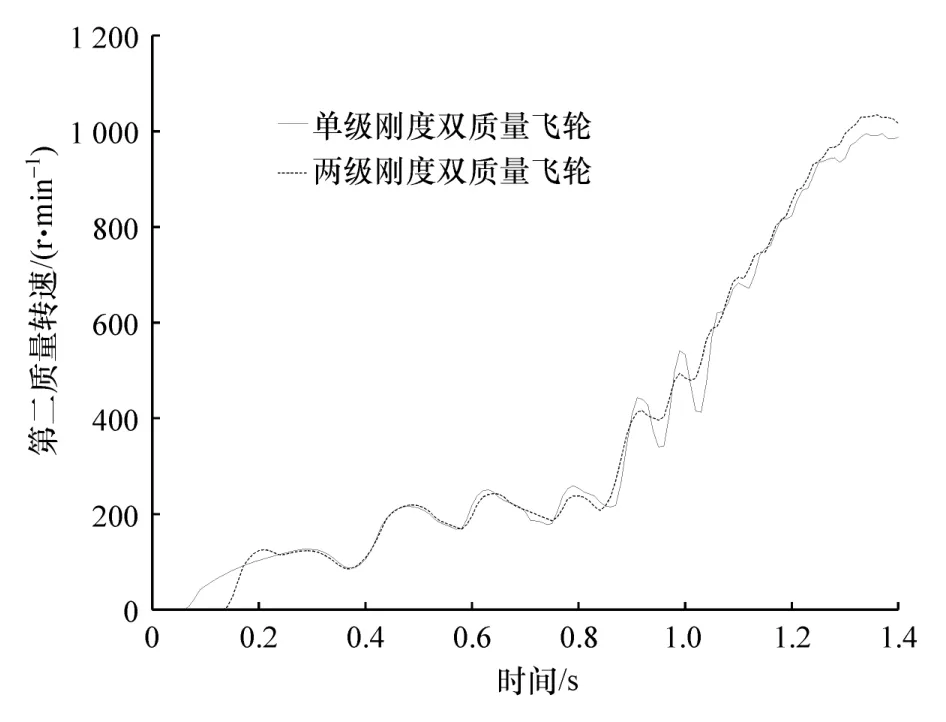
图11 第二质量转速波动图
4 仿真分析
本节利用AMEsim软件建立整车传动系模型,通过仿真对比分析单级刚度双质量飞轮和两级刚度双质量飞轮在相同工况下的隔振性能。本文中针对点火、熄火以及加速、减速工况进行仿真来对两种双质量飞轮的隔振性能进行对比分析。
4.1 点火工况
点火工况仿真模型如图10所示。单级刚度双质量飞轮的扭转刚度k1=8.03 N·m/(°)。
对装有单级刚度和两级刚度双质量飞轮的发动机进行仿真,获取起动过程中第二质量转速波动和角加速度,结果如图11和图12所示。其中单级刚度在模型中的实现是通过修改第1级刚度使其等于第2级刚度值。
由图11可见,在起动过程中,两级刚度双质量飞轮第二质量转速波动要比单级刚度的低,同时分析起动过程第二质量的角加速度也可以发现,两级刚度的表现要比单级刚度的好。通过计算角加速度均方根值,单级刚度第二质量角加速度值为199.0 rad/s2,两级刚度第二质量角加速度值为145.7 rad/s2,两级刚度要比单级刚度低26.78%,说明在起动工况下两级刚度双质量飞轮要比单级刚度隔振性能好,这也与第3节分析一致,这是由于起动过程中发动机转速会通过双质量飞轮的共振频率所对应的转速值,而前面分析的分段线性所发生的拐弯现象可以降低双质量飞轮的共振峰值,所以在起动工况下隔振性能好。
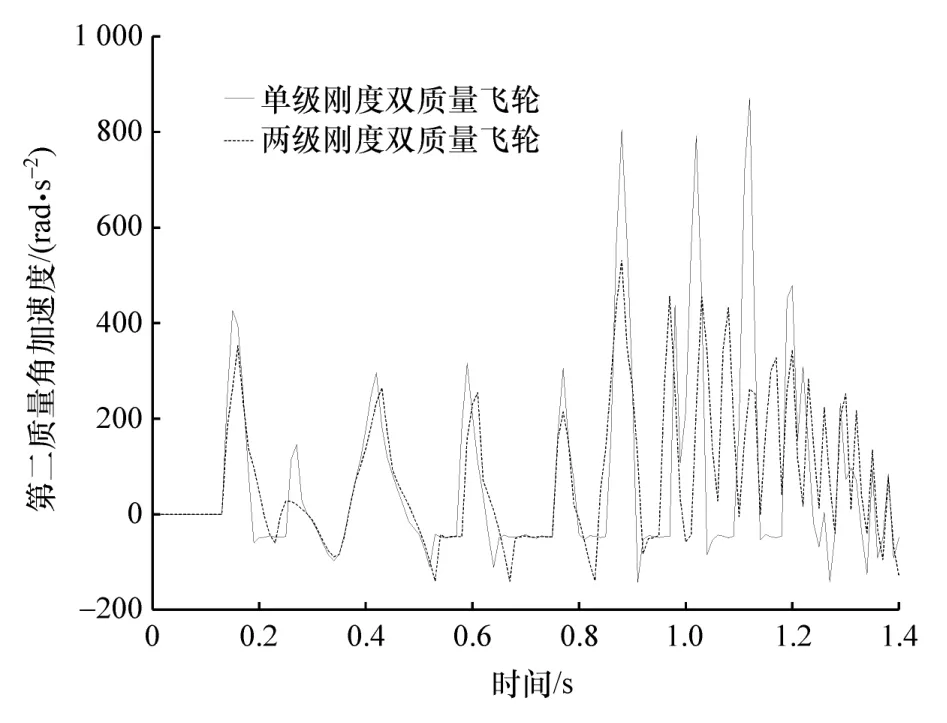
图12 第二质量角加速度波动图
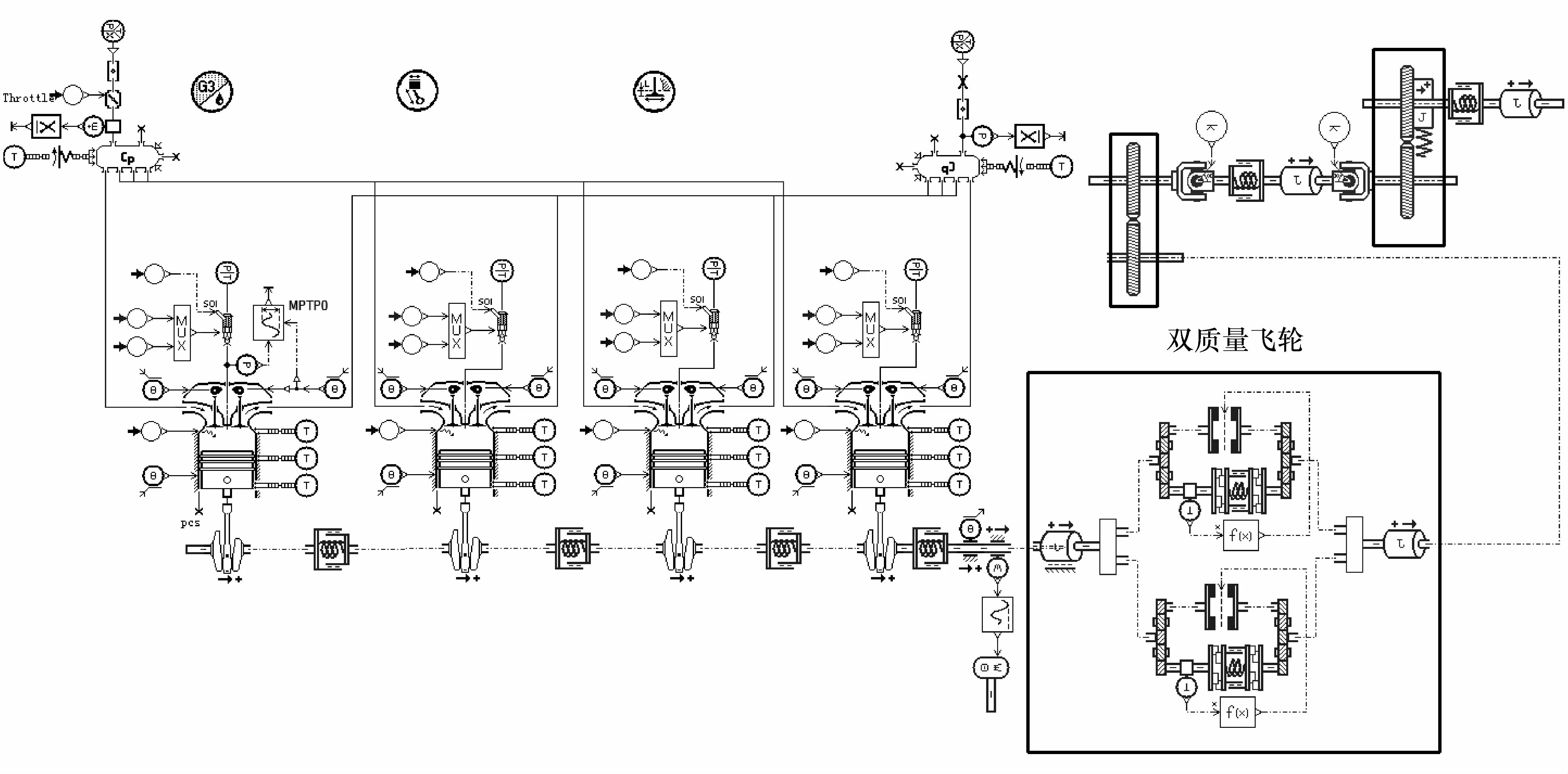
图13 加、减速工况仿真模型
4.2 加、减速工况
加减速工况仿真模型如图13所示,加、减速工况下单级刚度与两级刚度双质量飞轮的转速波动、角加速度波动分别如图14和图15所示。
通过加、减速工况的仿真结果可以发现,单级刚度和两级刚度双质量飞轮无明显差异。
4.3 熄火工况
熄火工况仿真模型与点火工况仿真模型一致,仿真结果如图16和图17所示。
通过图16可以发现,熄火工况下两级刚度双质量飞轮的第二质量转速波动要比单级刚度小,计算得到单级刚度第二质量角加速度均方根值为244.8 rad/s2,两级刚度第二质量角加速度值为171.7 rad/s2,两级刚度要比单级刚度低29.86%。两级刚度双质量飞轮在点火、熄火工况下隔振性能要比单级刚度好。
5 结论
本文中利用平均法求解双质量飞轮分段线性系统正弦激励下的一次近似解,从而得到其幅频特性函数并分析激励幅值、分布间隙、扭转刚度和阻尼系数对系统幅频特性的影响。
(1)通过建立双质量飞轮非线性动力学模型,利用平均法求解其正弦激励下的一次近似解,该方法适用于双质量飞轮的非线性振动分析。
(2)通过对幅频特性曲线分析,发现分段刚度双质量飞轮随着激励频率的变化,可能出现跳跃和滞后现象,这种现象可能会缩短双质量飞轮的使用寿命,所以合理设计多级双质量飞轮的结构、性能参数,使其共振带尽可能地避开发动机常用共振转速区间,从而可以提高双质量飞轮的使用寿命。
(3)通过对两级弹簧分布间隙、扭转刚度、阻尼和激励幅值等参数对双质量飞轮幅频特性的分析,发现阻尼系数、分布间隙和第2级扭转角刚度对幅频响应影响较大。
(4)利用AMEsim软件建立整车仿真模型,对比分析了单级刚度和两级刚度双质量飞轮在点火、熄火工况、加、减速工况下第二质量转速波动和角加速度波动值,发现两级刚度在点火、熄火工况下隔振性能更好。
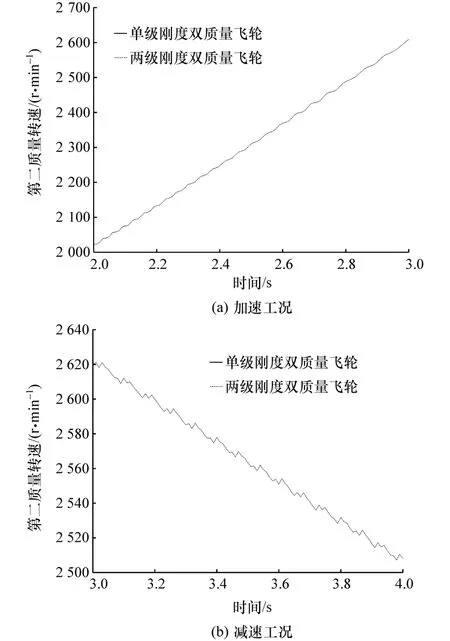
图14 加、减速工况第二质量转速波动图
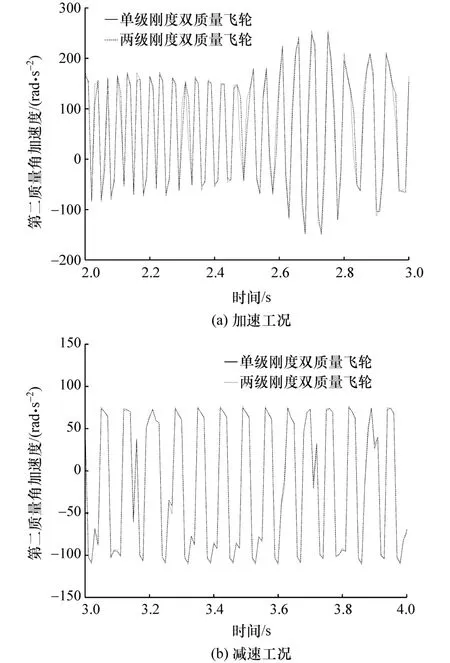
图15 加、减速工况第二质量角加速度波动图
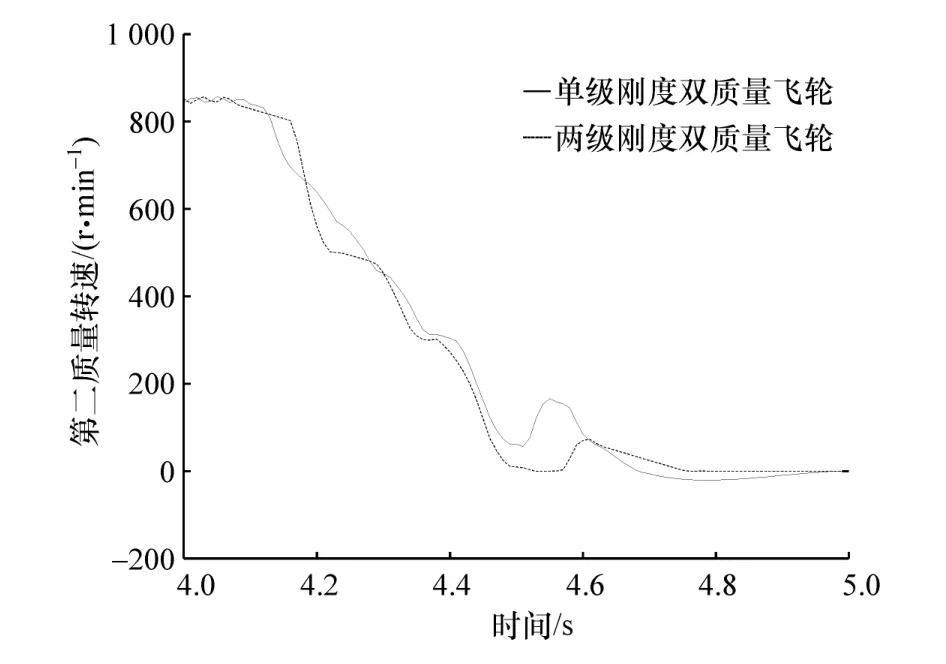
图16 第二质量转速波动图
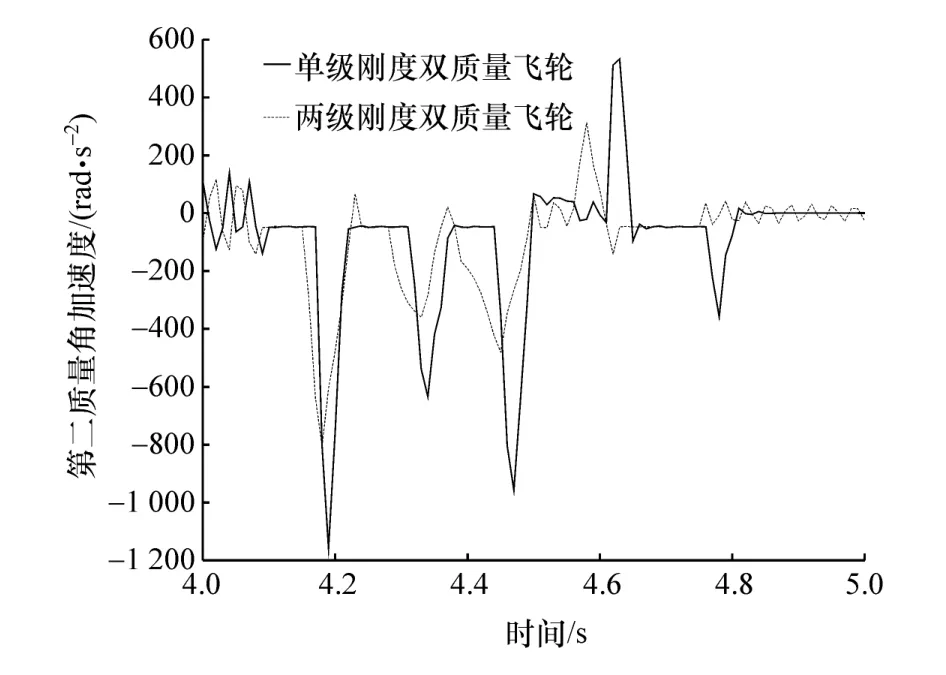
图17 第二质量角加速度波动图

