棱边强化薄壁方管静动态轴压理论和仿真研究*

郑玉卿，朱西产，马志雄

（1.湖州师范学院工学院，湖州 313000； 2.同济大学汽车学院，上海 201804）

前言

薄壁管件结构具有力学性能好、成本低、吸能效率高和相对密度低等优势，在汽车结构中有广泛的应用，当截面设计合理时，汽车高速碰撞过程中其能以稳定的塑性变形来耗散碰撞体的部分冲击动能，从而起到保护乘员舱结构和乘员安全的作用［1］。薄壁结构轴向压溃的研究始于20世纪60年代，Alexander［2］基于能量平衡法导出了整个轴向褶皱过程中的平均压溃力与圆管外径和壁厚之间的关系式，并通过试验数据拟合，确定了模型中的基本常数；之后 Johnson［3］，Abramowicz［4］，Singace［5］等对理论模型又做了不少修正和改进。Wierzbicki等［6］认为理想化的破损变形单元由水平固定铰和倾斜移行铰组成，获得了方管结构有效率与密实度之间的数值关系，理论结果与试验结果符合较好，并提出了方管1／4理想化折叠单元分析模型，更好地解释了薄壁方管轴向压溃过程中的能量吸收机理和力学特性。

其次，数值仿真技术已成为分析薄壁结构压溃特性的有效手段之一，尤其适合部分特征影响因子在物理试验无法测量或理论无法解析的情况。数值模拟可提取峰值压溃力、折叠长度、塑性变形量和分区能量吸收等，其中Langseth［7］等对方形薄壁铝管进行轴向压溃和碰撞仿真研究，Otubushin［8］和Marsolek［9］等使用LS-DYNA分别模拟了方管冲击过程和金属圆柱壳轴向压溃过程。上述研究均采用显式积分算法、四节点壳体减缩积分单元、壳体厚度方向设置多个积分点和沙漏控制技术来模拟薄壁结构的静动态压溃过程。王青春［10］和项玉江［11］等利用LSDYNA程序计算了薄壁管件准静态压溃，并提出了仿真精度改进措施和焊点模拟方法；朱西产等［12］通过轴向碰撞仿真和试验研究，分析了薄壁帽型梁结构的材料模型、应变率效应和点焊模拟方式对仿真精度的影响；王特捷等［13］对帽型梁进行落锤轴向冲击试验及有限元仿真，分析了其能量吸收特性。

上述薄壁结构研究成果均是基于单一材质属性分析所得，对异种材质的方管力学性能研究仍较少。嵇明［14］等论述了棱边强化440A单帽型结构在压弯作用下受压侧平板的弹塑性屈曲失稳过程和全截面抵抗力增强的影响因子，压弯试验和仿真分析均表明，其抗压和抗弯性能得到显著提高。本文在早期对棱边强化方管的静态压溃吸能特性［15］、力学特性［16］和应力强化敏感性［1］等相关研究的基础上，对棱边强化方管的轴向压溃理论进行归纳总结，辅以棱边塑性应变强化的方管轴向压溃试验进行验证，同时对棱边强化薄壁方管的动态轴向压溃特性展开理论分析和仿真研究，为棱边强化薄壁结构的强度设计和在车身结构中的工程应用提供理论支撑。

1 棱边强化方管轴向压溃理论

1.1 静态压溃理论

棱边强化（ridgelining strengthening，RS）方管的截面如图1所示，强化棱边用粗实线标出，平板母材用细实线标出。其中：c为平板部边长，s为强化棱边弧长，r为棱边部半径，a为方管总宽或名义边长（a＝c＋2r），h为方管壁厚。郑玉卿等［15］曾对棱边强化方管轴向压溃吸能特性进行了分项研究，分析了强化棱边对方管各部分变形区吸能的影响，本文中继续沿用其中的仿真模型，如图2所示，材料属性和边界条件不变，棱边部超高强化处理，平板部仍是母材，引入应力强化棱边与平板母材之间的屈服强度比为λ＝Yr／Yp，其中 Yr为超高强化棱边的屈服强度，Yp为平板母材的屈服强度。

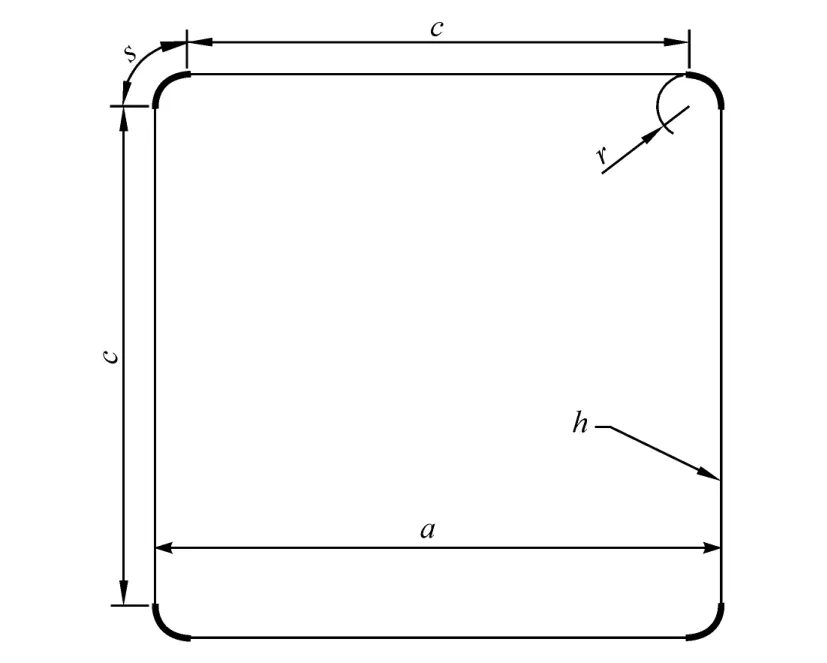
图1 棱边强化方管截面参数

图2 棱线强化方管数值仿真模型

文献［15］中经系列数学推导获得了理想压溃条件下棱边强化方管的平均压溃力计算公式：

式中：Pmr为棱边强化方管平均压溃力；M为单位长度塑性极限弯矩，M＝σ0h2／4，σ0为压溃过程中能量等效流动应力。

实际上，Abramowicz和Jones基于宽厚比a／h＝35～50系列软钢方管试验得到了每个折叠单元实际有效压溃距离一般为2H的0.77～0.78倍［4］，此处2H为一个基本折叠单元上下塑性铰之间的初始距离。故令本文的棱边强化方管有效压溃距离也为2H的0.77倍，则式（1）可改写为

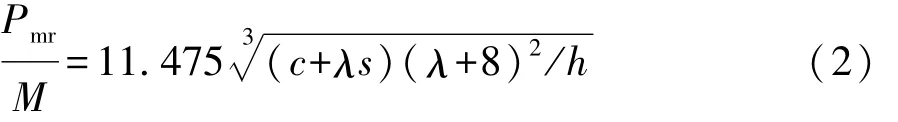
因此，式（2）为棱边强化方管准静态轴向压缩作用下的平均压溃力公式，其中形式上与Wierzbicki提出的原始材质平均压溃力公式［6］完全一致。

1.2 能量等效流动应力

计算单位塑性极限弯矩M＝σ0h2／4时，若材料为刚塑性材料模型，则假设能量等效流动应力σ0是一个随机常数。然而薄壁方管在轴压过程中，σ0实际是随塑性应变增大呈非线性增大，因此需要选取一个有代表性的平均应力值或函数来进行定义。流动应力一般被认为是介于屈服强度Y和极限抗拉强度Yu之间的某个值。例如 Wierzbicki［17］预测低碳钢方管轴向压溃性能采用了0.92Yu，得到的理论预测值与试验值更吻合；Kecman和 Suthurst［18］分析表明，薄壁矩形管一般在极限抗弯强度值时发生塑性弯折，极限抗弯强度由受压平板的屈曲应力或材料的屈服强度控制，且计算过程推荐使用极限抗拉强度Yu来代替流动应力；Kim T.H.等［19］则推荐基于受压平板的临界屈曲应力大小分级选用流动应力来预测薄壁结构的承载能力。薄壁方管受压平板的临界屈曲应力σcr和具体的分级选取准则为式中E为材料的弹性模量。

可见，无论薄壁结构在轴向压溃和弯曲过程中，塑性变形阶段的流动应力始终处于变化中，且介于材料屈服强度和抗拉强度之间。对于流动应力的大小，不同的材料具有不同的变化特性，暂无统一的选取准则，因此，本文中令σ0＝Y所计算出来的结果是相对保守的理论值。

1.3 仿真值与理论值对比

棱边强化方管仿真模型尺寸为h＝1.0 mm，a＝56.36 mm，E＝205.8 GPa，440A钢屈服强度 Y＝328 MPa，λ＝3.979。相关参数代入式（2）可得平均压溃力理论值为20.291 kN。同理，将h改为1.4和2.0 mm，其它参数不变，求得平均压溃力理论值分别为35.612和64.288 kN。其中，h＝1.0 mm棱边强化方管轴向压溃的最终塑性变形情况见图3，可见压溃过程中发生了预期的稳定塑性变形，其它壁厚的变形情况也类似。图4为壁厚h＝1.0，1.4和2.0 mm棱边强化方管的压溃力曲线对比。经仿真结果后处理获得了轴向压溃稳定阶段的仿真平均压溃力，分别为 20.717，36.062和 64.536 kN［16］。

图3 棱边强化方管静态压溃塑性变形

图4 轴向压溃力曲线对比

表1列出了静态平均压溃力仿真与理论结果的对比，偏差分别为2.1%，1.3%和0.4%。仿真与理论结果对比表明，式（2）能够较准确地预测棱边强化方管稳定压溃阶段的平均压溃力。若按整个仿真压溃过程取积分平均值，则为20.923，36.901和69.051 kN，分别比稳定阶段的平均压溃力提高2.0%，2.3%和6.9%，说明随着厚度增加，能量等效流动应力也是变化的，且都大于屈服强度Y，因此全局平均值略大于稳定阶段的平均压溃力。

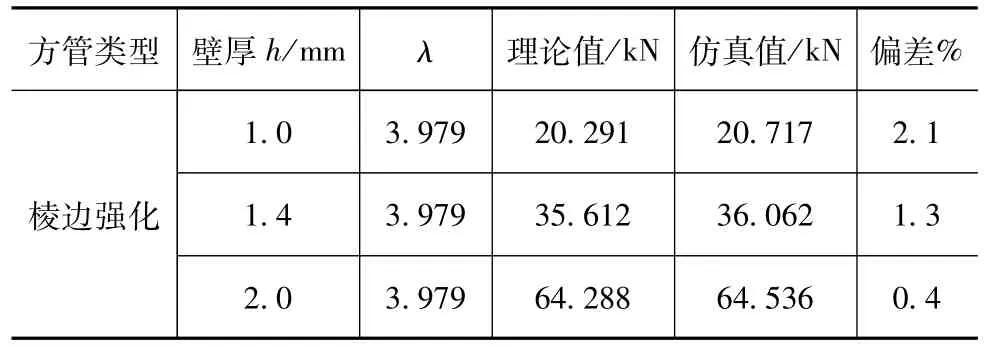
表1 静态平均压溃力对比

2 棱边强化方管动态压溃理论

2.1 动态压溃理论分析

因 M＝Yh2／4，将式（2）改写为

应变率效应属于钢材自身特有属性，其在方管动态压溃过程中起到了增强材料屈服应力的作用，应变率越大，屈服应力增幅越大，持续影响动态冲击过程的材料力学属性。根据Cowper-Symonds经验公式［20］：

式中：Yd为动态屈服应力；ε·为材料应变率；D为特征应变率；q为材料率敏感性的一个量度。常用的D＝40.4 s-1，q＝5是软钢冲击试验过程中屈服应力附近对应的小应变（ε＝0.05）情况下拟合得到的，因此较适用于冲击速度低于5 m／s的低速碰撞工况［20］。低碳钢中等应变率动态拉伸试验结果表明软钢屈服应力符合式（6）关系式，并拟合得到了D＝6844 s-1，q＝3.91［21］；而对于大量低碳钢方管在 4.4～10.7 m／s冲击试验过程中得到的动态平均压溃力，D＝802 s-1，q＝3.585代入计算所得理论值更符合平均动态试验值［5］。对于文献［14］中 RP350方管14 m／s的冲击试验结果［22］，采用 D＝6844 s-1，q＝3.91进行碰撞仿真得到的结果更接近试验值。因汽车碰撞过程，冲击速度较高，如C-NCAP规定正面碰撞最低速度为50 km／h，即 13.889 m／s［23］，参与碰撞的车身零部件塑性应变普遍大于0.05，且应变率甚至超过1 000 s-1，因此本文中也选用较高特征应变率D＝6844 s-1，q＝3.91来预测或模拟50 km／h碰撞工况，代入式（6）可得

式中Pdm为动态平均压溃力。

动态冲击情况下，很难精确计算应变率的数值，根据Abramowicz等理论推导，得到的对称压溃模式下平均应变率为

将 v0＝13889 mm／s，a＝56.36 mm，h＝2.0 mm代入式（10），可得棱边强化方管动态平均压溃力为85.315 kN。

2.2 动态压溃仿真分析

动态压溃过程仿真时，方管有限元网格不变，厚度为2.0 mm，材料基本属性相同，但须考虑金属材料应变率效应，设置Mat24模型中特征应变率参数D和敏感系数q。碰撞体质量为400 kg，通过增加Mass单元将质量平均分配到压板每个节点上，压板网格做了加密处理，平均尺寸为1.0 mm；为防止初始穿透，刚性压板与方管之间的间隙为1.0 mm；碰撞体初始速度设置为13 889 mm／s，且只能沿轴向运动，为模拟动态冲击全过程，计算总时间设为0.06 s，导入LSDYNA971求解器进行运算。为避免方管根部先发生崩塌失稳现象，受冲击端部单独切槽，用来诱导塑性变形。

2.2.1 塑性变形

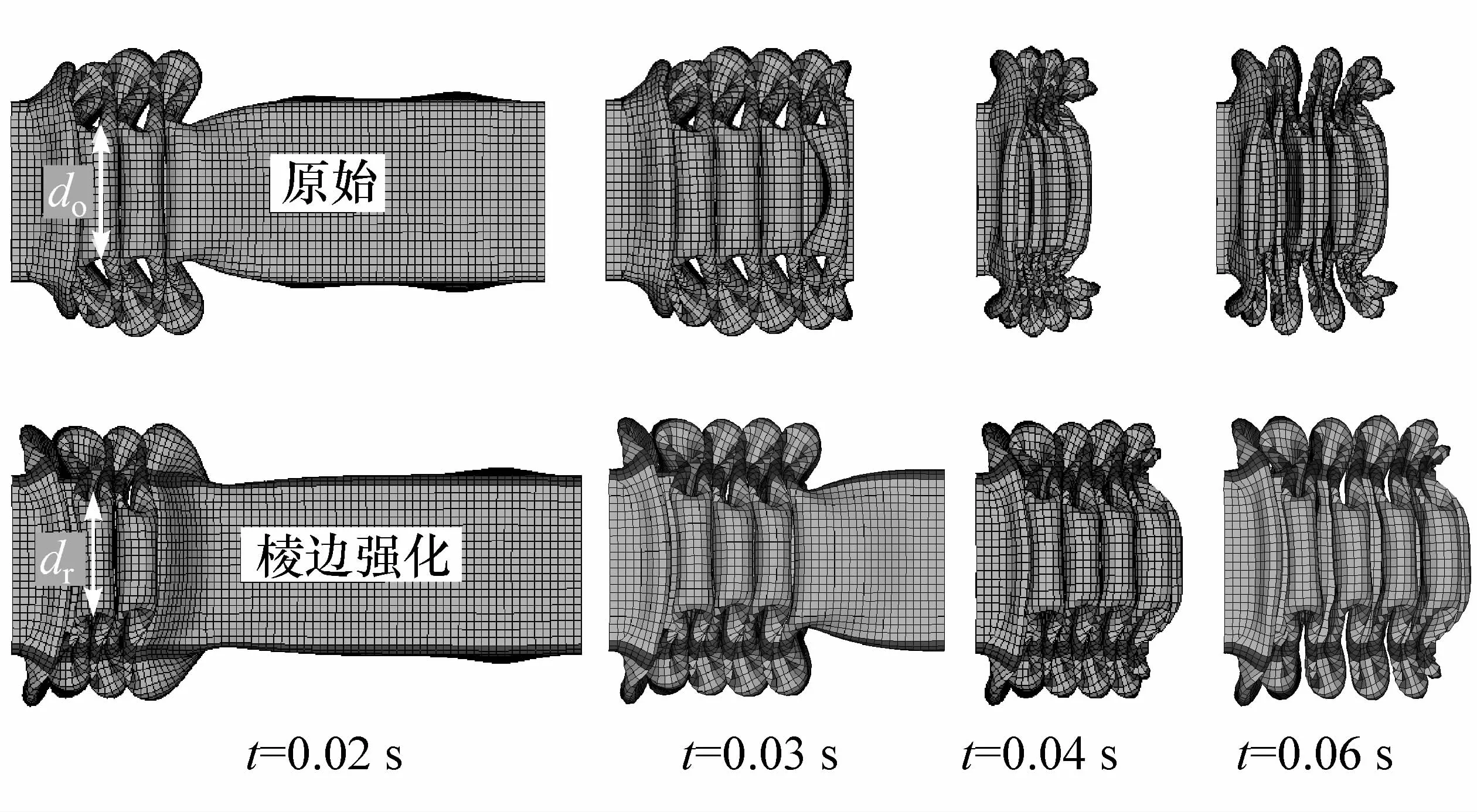
图5 原始方管和棱边强化方管动态压溃变形对比

式中：v0为碰撞体冲击方管前初速度；a为方管名义边长。对于其它非对称压溃模式，应变率表达式可参照文献［5］。

将式（9）代入式（8）可得50 km／h高速冲击时对称压溃模式下的棱边强化方管动态平均压溃力为

图5为原始方管和棱边强化方管动态轴向压溃过程的塑性变形对比。两者动态压溃过程塑性变形均为对称且稳定的，但原始方管褶皱单元宽度比棱边强化方管的更大，d0＞dr，其中d0为动态压溃过程中原始方管褶皱单元宽度，dr为棱边强化方管的褶皱单元宽度，说明棱边强化方管棱边部弯折长度更大，使得相邻的平板部塑性弯曲和拉伸更严重，故棱边强化方管平板部能量吸收速率也相对较高；t＝0.02 s和t＝0.03 s时刻的塑性变形对比表明，在同样碰撞条件下棱边强化方管动态轴向塑性压溃量比原始方管小；t＝0.04 s，原始方管已经被压实，而棱边强化方管并没有被压实，这说明棱边强化方管轴向抵抗力明显大于原始方管。刚性压板对原始方管和棱边强化方管停止压溃时间分别为0.04和0.044 s，因此0.04-0.06 s为原始方管褶皱单元的松弛阶段，而0.044-0.06 s为棱边强化方管褶皱单元的松弛阶段。

2.2.2 平均压溃力

平均压溃力是表征薄壁管静态或动态稳定压溃阶段的平均抗力水平。图6中分别为原始方管和棱边强化方管的动态压溃力曲线，其波动情况更好地解释了图5中方管动态轴向压溃过程塑性变形的演变过程。

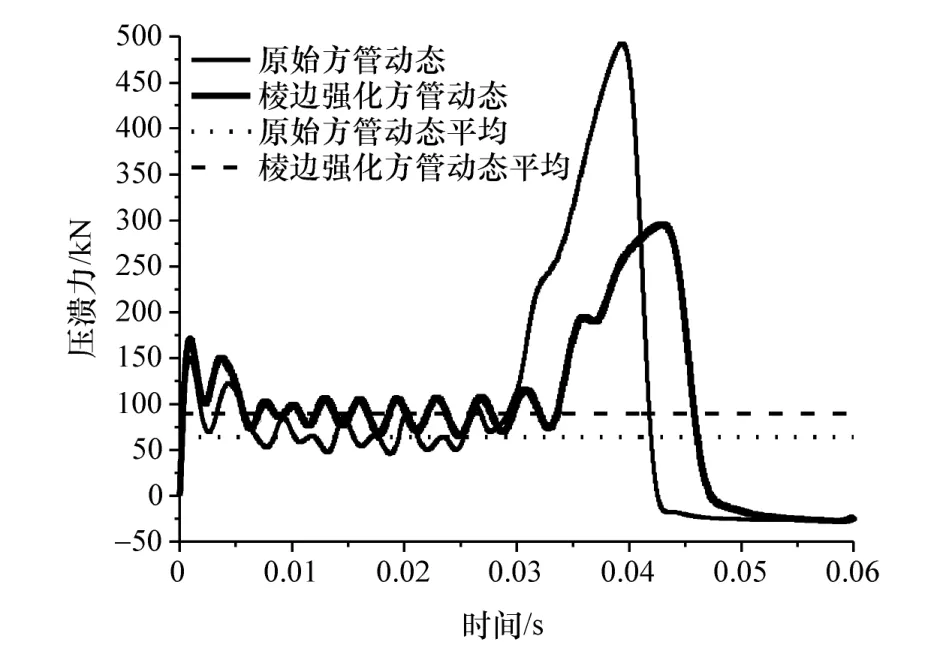
图6 动态压溃力曲线

原始方管和棱边强化方管的动态压溃力曲线在冲击初始阶段都出现了两个较高且不稳定的冲击波峰，在0.005 s之后进入了稳定的动态轴向压溃阶段，粗实线居于细实线上方，说明棱边强化方管抗力水平较高；0.03 s时细实线比粗实线率先进入褶皱压实阶段，压溃力也出现急剧上升，而粗实线在0.034 s时也出现了压溃力急剧上升。虽然粗实线峰值比细实线低，但表示平均值的粗虚线高于细虚线，说明在同样碰撞条件下，原始方管较软，轴向抵抗力较小，褶皱单元容易被快速压扁压实，同样压溃长度时吸能较少；两条曲线在峰值过后均出现了陡降，表明方管褶皱单元进入了自由松弛阶段，压溃力出现负值，刚性压板出现低速反弹现象。动态平均压溃力也同样对稳定的动态轴向压溃阶段取均值，原始方管动态平均压溃力为66.855 kN，而棱边强化方管的动态平均压溃力为88.743 kN。将仿真与理论预测结果均列于表2，计算原始方管和棱边强化方管的仿真与各自理论预测值之间的偏差，分别为2.9%和4.0%，这说明式（10）对棱边强化方管动态轴向冲击工况下动态平均压溃力的预测效果也较好。

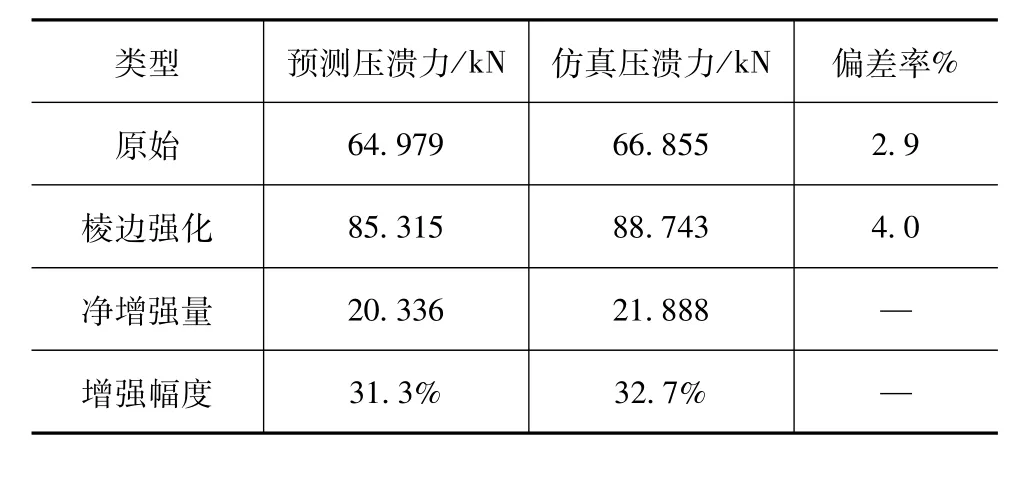
表2 50 km／h碰撞速度时方管动态平均压溃力对比

3 静态压溃试验验证

3.1 棱边塑性应变强化现象验证

令λ＝1，可求出原始方管理论预测值，与文献［4］中的低碳钢方管试验值对比发现，理论值明显低于试验值，这是因式（2）是基于方管所有部位材质属性相同的前提下导出的，实际上原始方管在加工成形过程中，棱边部弯折成直角过程存在一定程度的塑性强化现象，其次是轴向压溃过程中流动应力的影响。

为验证这一塑性强化现象和式（2）的合理性，且考虑到35钢材料力学性能与440A力学性能较为接近，购置 35冷轧钢板一块，长、宽、厚分别为2 500，1 250和1.2 mm，利用线切割裁取了标准拉伸试件和长、宽分别为200和10 mm的平板条试件，并利用折弯机将35钢平板条折弯加工成直角棱边试件（截面形状与角钢相似），厚度均为1.2 mm，加工好的试验样件如图7所示。

图7 35钢平板和直角棱边拉伸试件

之后用万能试验机对标准拉伸试件和直角棱边试件进行重复多次单向拉伸试验，拉伸速度为5 mm／min，拉伸应力 应变曲线如图8所示。

图8 工程应力应变曲线

显然直角折弯工艺导致10 mm宽的棱边部屈服强度由389提升至726 MPa左右，且延伸率有所降低。需要特别指出的是，图8中弯折棱边拉伸曲线高度是受试件宽度影响的，它会随着试样宽度的增加而整体下降，屈服强度也会随宽度的增加而降低，因此可推测棱边部由于直角弯折应变，中间的屈服强度最高，两边逐渐过渡到平板母材屈服强度。

图9 35方管轴向压溃试验

3.2 静态压溃理论验证

通过平板裁剪、人工折弯和焊接操作，制作了截面长、宽均值分别为 56.9和 57.0 mm，壁厚为1.2 mm的棱边塑性应变强化35方管若干根，两侧平板部中部采用CO2气体保护焊封闭，长度为300±2.0 mm，仍采用万能试验机重复进行3次静态压缩试验，如图9所示。试验速度为5 mm／min，获得的压溃力试验曲线如图10所示。由图可见，压溃过程方管形成了稳定的褶皱单元，平均压溃力见图中直虚线，试验值约为29.786 kN。

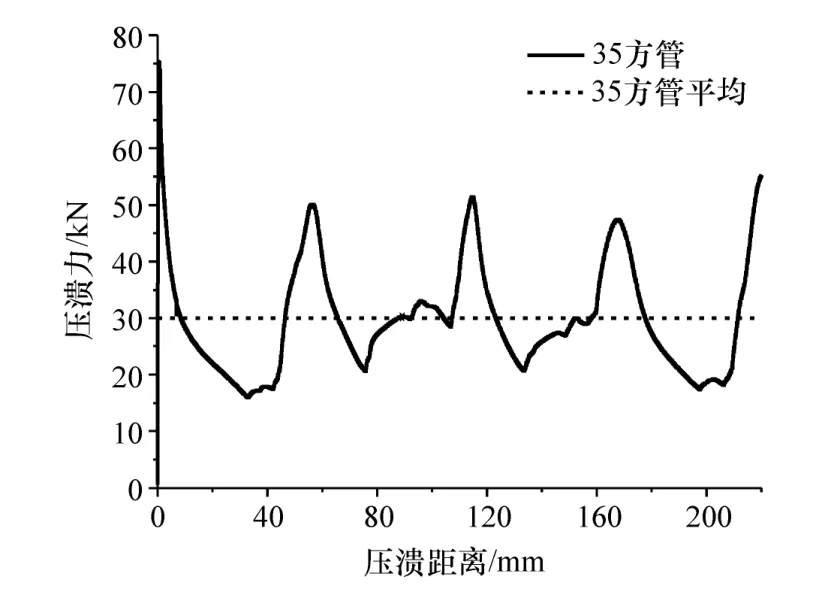
图10 35方管试验压溃力曲线

35钢制方管参数为 s≈10 mm，r＝6.37 mm，c＝44.26 mm，λ≈1.866，代入式（2）求得理论压溃力为27.667 kN，比试验值低7.1%。将试验结果和Q235方管试验结果［15］一同列于表3，可见理论预测值接近试验值。试验值偏大，可能与实际方管的两个平板部存有焊缝硬化有一定关联，且方管压溃过程中能量等效流动应力势必会随塑性应变增加而呈幂函数曲线增大，因此式（2）采用屈服强度替代流动应力来预测平均压溃力，结果本身就偏于保守。35钢制方管和Q235棱边塑性应变强化方管静态轴向压溃试验不仅验证了式（2）的有效性，且还可根据试验值反求出能量等效流动应力σ0值分别为418.8和279.1 MPa。

表3 理论值与试验值对比

4 结论与展望

（1）引入原始方管和棱边强化方管静态平均压溃力统一预测公式，讨论了能量等效流动应力σ0对理论预测结果的影响，然后结合Cowper-Symonds经验公式，建立了棱边强化方管动态平均压溃力预测公式。数值仿真再现了静动态轴向压溃过程，分析了强化棱边对方管塑性变形和平均压溃力的影响。静动态仿真值与理论值均吻合较好，偏差最大不超过4%。

（2）35方管和Q235方管物理试验验证了方管成形过程中的直角弯折棱边塑性应变强化现象，同时也验证了静态平均压溃力预测公式的预测精度，能量等效流动应力均值可根据试验值反求得到。

（3）棱边应力强化技术的主要优点是在不增加零部件质量的前提下，提高薄壁结构的截面抗力水平，实现轻量化设计。对于低强度级别钢板可采用普通模具冷冲压加工，然后根据零部件碰撞载荷需要进行局部超高应力强化，从而提高零部件抗压弯性能，力争替代车身中不断上升的超高强度钢零部件，降低综合制造工艺成本。