多自由度球形感应电机创新设计及其参数化仿真分析*
邓 涛,苏振华,唐 鹏,姜 路
(重庆交通大学机电与车辆工程学院,重庆 400074)
前言
对于车用电机而言,无论是直线电机还是旋转电机,都只能驱动1个自由度。纯电动汽车、混合动力汽车、插电式混合动力汽车等新能源汽车也绝大多数采用单自由度旋转电机作为驱动单元的组成部分,而诸如全向汽车、智能网联汽车等未来汽车,需要驱动更多自由度来实现相应的功能。经典解决方案是使用机械传动机构对几台电动机进行组合,如使用万向轮[1]或机械并联机构[2]。这样的结构往往复杂而沉重,降低了其动态性能,增加了控制的复杂程度。
多自由度电机的出现冲破了传统电机设计的固有思维,扩展了电机应用的领域,国内外学者也纷纷对其进行了相关的研究。Kaneko等人[3]通过在转子铁轭上固定4个永磁体,同时在定子上布置3套绕组,运用微机控制3套绕组的电流,从而对电机转矩的大小和方向进行控制,实现3自由度运动,但整个机构比较复杂。Kumagai等人[4-5]分别研究了直线感应电机、3自由度平板感应电机和3自由度球形感应电机,由简到繁,从设计和控制层面对多自由度电机进行了较为全面的阐述。Ueno等人[6]提出使用铁镓合金为材料的微型球形电机,通过推拉活杆使转子产生转矩,可作为旋转摄像机的微型执行器。Toyama等人[7]利用超声波原理对球形转子进行驱动,在相对较低的转速旋转时,实现高精度控制。国内的研究主要以永磁球形电机和超声波球形电机为主,虽起步较晚,但也得到了一些成果。王群京等人[8-9]主要进行永磁球形电机的控制算法设计和转子的位置检测研究。傅平等人[10]对2自由度行波型超声波电机的机理展开了研究和优化设计,提高了超声波球形电机的参数性能。
综上所述,国内外对于球形电机控制算法的研究较为深入,但对其本源设计和理论研究涉及较少。本文中在直线感应电机的理论设计基础上,以城市代步用微型电动车为参照对象,对多自由度球形感应电机进行尺寸设计,其构型如图1所示,由3个均匀分布的弧面定子和转子球壳组成,通过独立控制3个定子来对2个旋转自由度进行驱动,实现转子的多自由度旋转,从而使微型电动车可达到全方位转向的功能。
同时,为进一步满足实际需求,基于 ANSYS Maxwell软件对多自由度球形感应电机进行建模和电磁瞬态仿真分析,通过仿真数据与设计值的对比,来验证设计的正确性。并对多自由度球形感应电机进行参数化分析,得到其在不同电压、不同频率下的特性曲线。其设计流程如图2所示。
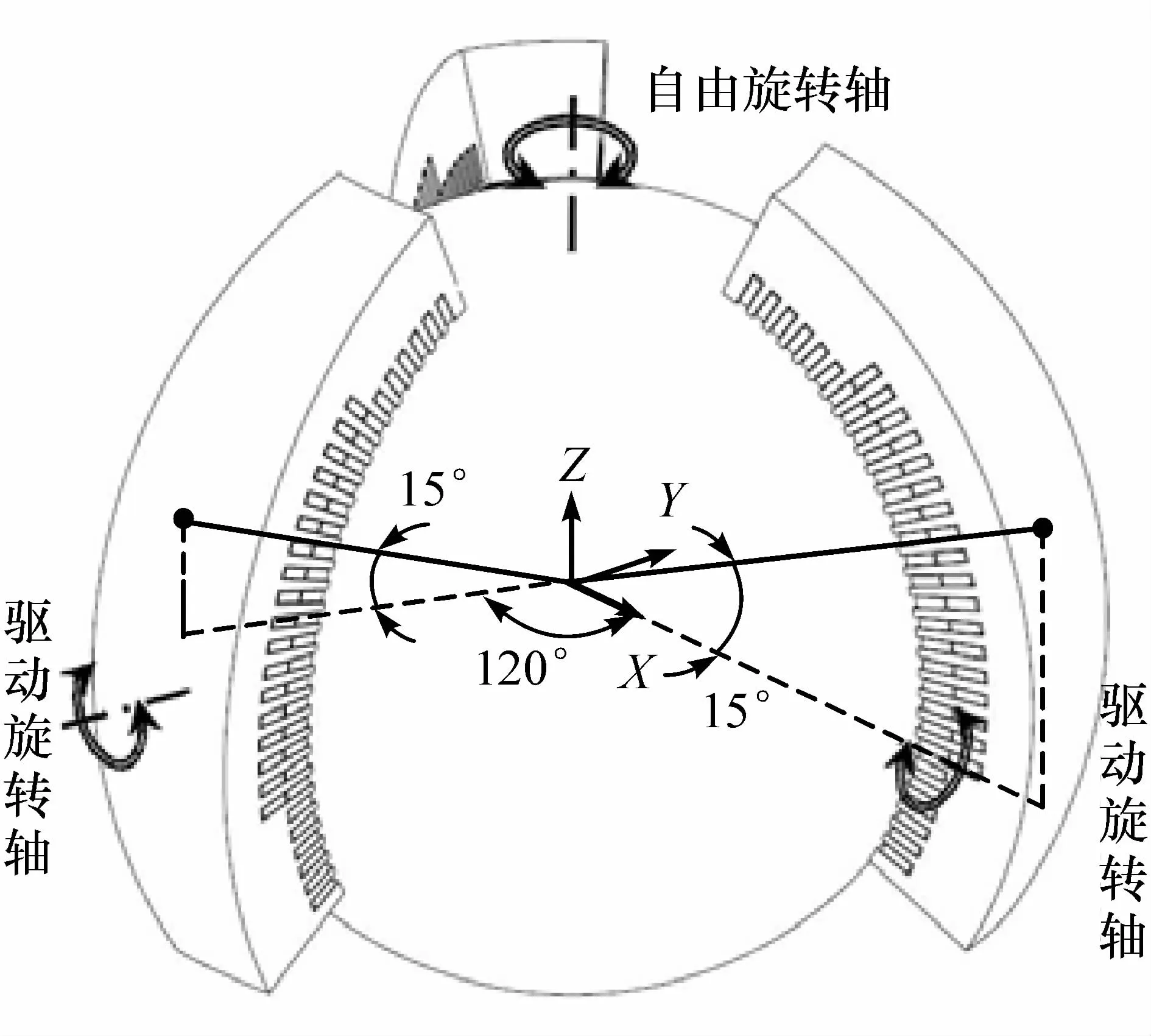
图1 多自由度球形感应电机

图2 设计流程图
1 尺寸参数的确定
由于本文中设计的球形感应电机定子结构与直线感应电机定子结构相类似,可根据直线感应电机电磁设计方法来确定球形感应电机的主要尺寸。先确定等效的直线电机尺寸,再将其圆弧化形成弧形直线电机,最后将弧形直线电机球面化形成球形电机。直线电机的原始数据如表1所示。
1.1 主要尺寸的确定
1.1.1 电磁负荷的选取
为减少损耗和降低磁化电流,直流感应电机的磁负荷应取得低一些,且此电机是持续负载,电负荷AS不应取过高,因此,选取:气隙磁通密度 Bδ=0.25 T;初级电负荷 AS=20 kA/m。
1.1.2 初级主要尺寸和绕组布置形式的确定经计算得到的主要尺寸如表2所示。

表1 直线感应电机设计原始数据

表2 初级主要尺寸参数
1.1.3 气隙和次级导体尺寸
(1)次级导体宽2c

(3)气隙δ和次级导电板厚度d的确定
气隙δ和次级导电板厚度d的确定是设计中的关键问题,由以下两个公式联立求得

级绕组每相漏抗
式中:ρ2为20℃时次级导体的电阻系数;cosθi为内功率因数;s为滑差率;μ0为空气磁导率;kw1为绕组系数;pe为等值极对数;kE为反电动势系数;r1为初级每相电阻;kβ为感应电机系数;λs为槽漏磁导;λe为初级绕组端部漏磁导。
将各参数代入式(1)和式(2),可得到两条曲线,如图3所示。
两条曲线交于(2.8,7.964),表示气隙和次级导体厚度的尺寸,选取次级导体厚度d=8 mm,次级导体材料为铜。在气隙尺寸选取方面,由于该设计公式主要应用于直线感应电机,其气隙取得较大,而本文中研究的是以旋转磁场为主、其径向波动较小且有球形轴承作相应的支承,因此,气隙可取小一些,取 δ=2 mm。

图3 δ-d曲线
1.1.4 弧形直线感应电机尺寸的确定
经计算,直线感应电机主要尺寸已经确定,因此将其圆弧化,使直线电机的行波磁场转换为弧形直线电机的旋转磁场。由于城市代步微型电动车的轮毂外径约0.3 m,因此取弧形电机的转子外径为0.3 m,其它尺寸参数不变,得到的弧形电机的平面模型如图4所示。

图4 弧形直线电机2D模型
由于将行波磁场转化为旋转磁场,之前输出的额定推力将转换为额定转矩,同步速度将转化为同步转速,据此得到弧形直线电机的频定转矩为7.5 N·m,同步转速为 764 r/min。
2 ANSYSMaxwell仿真分析
2.1 弧形直线感应电机仿真
将计算得到的各个参数尺寸,通过ANSYSMaxwell 2D中的Transient求解器,忽略弧形直线感应电机的横向边端效应,采用运动表面算法对做旋转运动的弧形直线感应电机进行瞬态仿真。建模过程主要分为生成几何模型、选定材料、设定激励源和边界条件、定义执行参数和定义求解选项。将图4中的弧形直线感应电机模型导入ANSYS Maxwell 2D design中,添加region求解域和band运动域后,经过上述前处理过程,得到求解前模型,如图5所示。
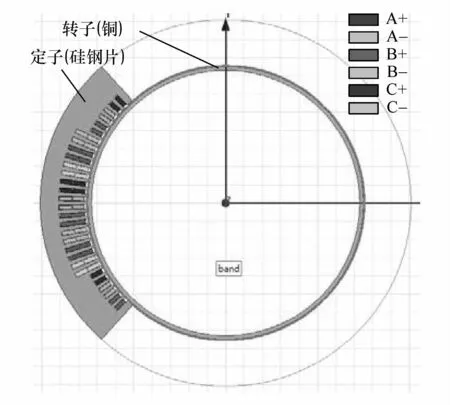
图5 弧形直线电机求解前模型
设置求解器以后,运行求解模型,得到的仿真结果如图6~图8所示。

图6 磁力线仿真分布

图7 转矩、转速随时间变化曲线(空载)
由图6可见,磁力线由定子轭、定子齿进入气隙后穿入转子导体板,再从另一个定子齿进入定子轭,形成一个极的闭合磁力线。图6中含有5个极,其中4个完整的极和1个两端分开的极,两端磁力线通过空气闭合,其极数与设计值相符。图7为空载时弧形电机转矩、转速随时间变化曲线,转子上所产生的转矩在约40 ms后处于稳态,转速稳定于772 r/min;图8为额定负载时弧形电机转矩、转速随时间变化曲线。转子上所产生的转矩在约40 ms后稳定于7.5 N·m(额定转矩),转速稳定于 624 r/min。其空载和负载过程得到的仿真结果与设计值之间的偏差小于1%,满足设计要求,因此,设计的尺寸参数是合理的。

图8 转矩、转速随时间变化曲线(负载T=7.5 N·m)
2.2 球形直线感应电机仿真
经对设计尺寸的验证,将弧形感应电机球面化,对球形感应电机进行三维建模,为简化分析过程,只对单定子的电磁场进行分析,得到的模型如图9所示。

图9 球形感应电机3D模型(单定子)
将图9中的球形直线感应电机模型导入ANSYS Maxwell 3D design中,添加region求解域和band运动域后,进行前处理,并对其进行求解。得到的仿真结果如图10所示。
由图10可见,球形感应电机在负载为7.5 N·m时,转矩可稳定于 7.5 N·m,转速可稳定于625 r/min,其仿真结果与弧形感应电机二维仿真结果类似,不同点在于达到稳态的时间增长,电机启动时转矩波动更为明显,其原因为:首先,球形转子的转动惯量大于环形转子,导致球形转子的角加速度较小,使其到达稳态的时间增长;其次,将弧形电机球面化以后,其磁场由二维轴向叠加的磁场转化为三维磁场,这样会导致电机在启动时磁场更为无序,且响应时间较长;此外,球形感应电机由于转子是球形的,故可将其转子的宽度视为无限宽,其纵向端部效应和横向端部效应都将发生变化,使气隙磁密的幅值沿导体移动方向发生畸变,使电机的特性变差,难以迅速达到稳态。
通过对单定子球形感应电机进行仿真,得到上述结果符合理论要求,而对于三定子的组合,可结合理论计算进行分析来得到其转矩分配情况。其关系如式(3)所示。由式(3)可得:若要绕x轴产生1 N·m的转矩,则f2与f3所对应的定子应在球形转子上分别产生0.577和-0.577 N·m的转矩。而其它转矩大小和方向的变换均可通过式(3)进行换算。

图10 转矩、转速随时间变化曲线(负载T=7.5 N·m)

式中:fi为各定子在球形转子上所产生转矩,i=1,2,3;τx为绕 x轴所需转矩;τy为绕y轴所需转矩。
经计算,在220 V三相电压、频率为125 Hz的额定条件下,将4个多自由度球形感应电机应用于微型电动车,使该车正常沿直线行驶,该车可在37.5 km/h的车速下产生60 N·m的转矩,对于车辆在城市工况下的正常行驶是适用的。
而在参数化分析中,为简化模型,缩短计算时间,可用弧形感应电机的二维模型代替球形感应电机的三维模型进行求解。
3 参数化分析
为检验所设计电机参数的合理性,应观测其它参数变化时电机的性能如何变化,因此可对其进行参数化分析。目前汽车行业常通过改变电压电流的方式来实现对旋转电机转矩的控制;通过变频控制,即改变电源频率来调节电机转速。因此,在ANSYS Maxwell中进行参数化分析时,可将电源电压或频率设置成线性函数,得到在不同电压或频率下转矩与转速和功率与转速的关系曲线。
3.1 电压参数化分析
将输入电压和转速作为参数进行分析,取220-380 V、间隔为20 V的离散电压参数和0-764 r/min、间隔50 r/min的离散转速参数作为分析对象,得到的电压参数化分析结果如图11和图12所示。

图11 不同电压下转速与转矩关系曲线

图12 不同电压下转速与输出功率关系曲线
由图可见,随着电压的升高,转子球壳产生的转矩增大,同时由于输入功率的提升,输出功率也随之提升。对于本文中设计的球形电机而言,结合上述分析的结果,可通过改变绕组中通入的电压(或电流)来控制转矩。进一步来说,由于3个定子驱动单元是独立的,故各个定子能通入不同的电压来产生不同的转矩,通过转矩的合成便可改变总转矩的方向,实现转子可绕xy平面中过O点的任意轴进行旋转运动,同时可随时改变旋转轴的方向。
3.2 频率参数化分析
将频率和转速作为参数进行分析,取75-175 Hz、间隔为25 Hz的离散频率参数作为分析对象,在尺寸不变的前提下,球形感应电机的同步转速也会因频率的改变而变化。

式中:f为频率;τ为极距;r为转子球壳半径;ns为同步转速。
各频率下的同步转速如表3所示。因此转速参数的选取根据表3中同步转速的值进行等分选取。

表3 各频率对应同步转速数据
频率参数化分析结果如图13和图14所示。

图13 不同频率下转速与转矩关系曲线
由图13可见,随着频率的提高,转速的范围变宽,但同一转速所对应的转矩减小。由图14可见,随着频率的降低,转速范围变窄,输出功率有所增加,从侧面反映出频率的降低有助于效率的提升。上述仿真结果也表明通过改变频率来调节转速范围是可行的,因此,可同时改变各定子中电压的频率来实现转速范围的调控,从而控制转速变化。
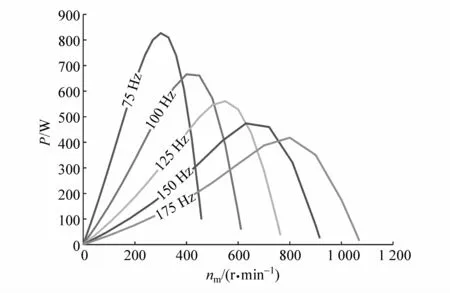
图14 不同频率下转速与输出功率关系曲线
4 结论
对传统电机进行了创新性设计,将城市代步用微型电动汽车作为应用对象,从理论和仿真两个方面论证了用多自由度球形感应电机来驱动全向车轮的可行性,实现全方位转向的功能。
(1)基于直线感应电机设计理论,对球形感应电机的尺寸进行设计,并在后续的仿真中验证了尺寸的正确性。
(2)运用ANSYSMaxwell软件对弧形感应电机和球形感应电机进行了二维和三维的电磁场瞬态仿真,得到的仿真数据与设计值相对应。
(3)对所设计的球形感应电机进行了参数化分析,得到不同电压和不同频率下转速与转矩和转速与功率之间的关系,通过分析可知,转矩随输入电压的提升而增大,转速范围随频率的提高而扩大。
后续的研究中,将加入转矩/转速控制模块来模拟城市工况的实时性影响,并搭建实物实验平台,对多定子产生的转矩/转速进行台架测试,观测多定子产生的耦合磁场对球形转子带来的影响,以验证理论计算与仿真结果的正确性。

