基于证据理论的多模型事故再现结果融合*

邹铁方，刘 勇，何枫林，李 华

（1.长沙理工大学汽车与机械工程学院，长沙 410114； 2.都柏林圣三一学院机械与制造工程系，都柏林爱尔兰 999015；3.湖南省工程车辆安全性设计与可靠性技术重点实验室，长沙 410114）

前言

事故再现是依据事故现场所遗留的各类痕迹并参考证人证言等其它证据对事故发生全过程进行推断［1］，再现结果不仅能为事故责任认定提供依据［2-3］，还能为车辆安全、交通安全等领域提供大量有价值的基础数据［4-7］，因而近年来备受关注。但受制于人们认知的局限性，目前尚无模型可以保证其所得结果绝对正确，随着外部条件的改变原本效果不错的模型也会失效［8］，如再考虑模型所需痕迹具有不确定性［9-10］，则其可靠性更低。人们积极寻找更为准确的事故再现模型，依据文献［9］中的分类，事故再现有车辆制动痕迹［11］、行人抛距［11-12］、车体变形［13-14］、人体损伤和综合仿真［15-18］等方法。近年来随着技术手段的进步，基于车载设备如车速表、安全气囊数据及基于视频监控的相关再现技术被引入［19-22］，极大地丰富了事故再现中模型的种类，使再现人员在任何情况下均有多种模型可选。但事故再现中的本质问题依然没有解决，即目前所有模型均无法保证其所得结果绝对正确。这就使得事故再现人员更愿意选择多个模型对同一事故进行再现，如文献［23］中所述则选用了3种方法，最终确定所得结果约为106 km／h。这引发出一个问题，即“约为106 km／h”是如何得到的？这本质上是多模型所得结果最终如何表述的问题？批评者认为这不是一个问题，因为如果痕迹多则可通过相互验证［24］将错误结果删除；还有学者认为事故再现者应关注于更精确的模型和痕迹，因这两者如不准确则多模型结果表述问题就无价值。殊不知基于现有技术手段，很难依靠某一模型将另一模型所得结果完全否决。而从痕迹、模型入手自然可从本质上提升再现结果的可靠性，但这不能否定不确定分析技术能提升再现结果客观性的事实。当降低痕迹不确定性、提升模型精度和交叉验证等均未能进一步提升再现结果可靠性时，多个模型所得结果如何描述依然是一个客观存在的问题［25］，有待进一步研究、探索。

1 问题描述

事故再现是指根据事故现场痕迹，依据模型计算从而获得事故碰撞结果，其数学形式可表示为

式中：Y为事故再现结果；f为事故再现模型；X为模型所需痕迹。

因事故现场痕迹受外界因素影响会慢慢消逝而导致X不确定，因认知局限会导致f不确定，这样将会直接导致Y不确定。为降低Y的不确定性，人们更愿意从痕迹、模型入手展开研究。痕迹方面，从最初的测量误差研究［26］到后期引入先进测量技术如航拍和3D扫描［27-28］等以便快速准确获得X。模型方面，如上所述，人们不仅在传统领域继续研究［29］，还引入新技术和新方法［30］以获得更精确、更可靠的f。显然这些工作是有效的，已从本质上提高了事故再现结果的可靠性。但一个不容忽视的事实是，依然无人敢保证其所测得的痕迹或依据某一模型所获得的结果绝对正确。如文献［25］中用了4种方法获得5个车速结果，其中基于EDR和车速表指针的结果被公认为最可靠，结果分别为24.44和23.33 m／s，但孰优孰劣恐怕很难论断。而依据经验公式所得最大速度为28.63 m／s，看起来与其它结果相差较大，但恐怕也很难简单地通过交叉验证而否定它，毕竟事故发生时事故现场环境无法准确还原。这说明事故再现中的不确定性问题是客观存在的，不能视而不见。为降低Y的不确定性，降低痕迹、模型的不确定性为首选；其次为选择合理方法（如文献［24］中的方法）对痕迹、模型所得结果进行验证后排除错误信息；当这些方法均不能彻底消除Y的不确定性后，则可选择不确定性分析方法［31-33］将痕迹不确定性反映到再现结果中去，并选择合理的表述方法对所得多个事故再现结果进行描述，以提高再现结果的客观性。

对多个模型结果进行合理描述是实践的需要。无论是将再现结果运用在事故鉴定领域还是安全研究领域，人们希望获得的结果是一个易于理解的值，而不是如“依据某模型得某速度”之类的系列值。这在模型验证中同样需要，如依据同一物理试验中不同视频资料验证仿真软件的某一性能时［34-35］，获得“依据某视频获得的误差为某”等系列结果也不合适。这表明，对多模型即不同方法所得多个结果进行合理表述具有研究价值。

为此，本研究重点关注多模型所得多结果如何描述的问题。这个问题可非常简单地处理，比如多个结果取均值、取多个结果的最值组成区间等。但需要思考的是，有没有更有说服力、理论上更可靠的描述方法呢？答案是肯定的，无论是模型还是痕迹均可视为支持再现结果的证据，模型和痕迹多表明证据多，将它们按照一定方法融合即可，而证据理论恰好具有这样的功能。

2 证据理论

证据理论一般是指Dempster-Shafer（DS）证据理论，最先由Dempster提出［36］。它为决策不确定信息的表征与融合提供强有力的工具，在相关领域展现出良好的应用效果［37-40］。辨识框架是证据理论的最基本概念。对于一个问题而言，其所有可能结果构成的辨识框架用Θ表示，Θ是一个非空集合。Θ中所有子集的组合称为幂集，用2Θ表示。对于辨识框架 Θ＝｛A，B，C｝而言，它的幂集为

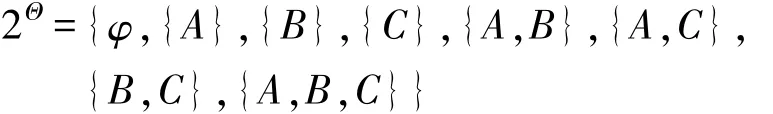
证据理论中另一重要概念是基本概率分配（basic probability assignment，BPA），可记为

如果 m（A）≠0，则称 A为焦元。在证据理论中，事件中所有可获得的信息均可视为证据，而这些证据可依据证据合成规则进行融合，最初的融合规则由Dempster提出。假设 m1，m2，…，mn是辨识框架内的 n个 BPA，与之对应的焦元为 Ai（i＝1，2，…，n），则

为冲突系数，K越大则表示证据之间冲突越明显，当K＝1时证据间高度冲突，式（3）失效。此时有很多改进方法可供选择［41-42］，本文中仅给出一种易于操作的方法以应对高冲突证据。对于一个有m焦元的问题，将它们的BPA修改为

如此则式（3）依然可用。

3 基于证据理论的多模型事故再现结果融合方法

假设对于某一事故，选用了n个模型（或方法）进行再现，则式（1）可表示为

即n结果构成一辨识框架，如知道与之对应的BPA值，则将相关结果融合成一个结果不失为描述多结果的一种方法，即

显然，这一步的核心在于确定BPA即m（Yi）的值。

（1）第1种方案 认为选用的i模型对自身所得结果100%支持，但对其它模型所得结果则不支持。故可得BPA矩阵，如表1所示。

表1 BPA矩阵

然后对证据进行融合。以n＝2为例，此时模型1对应的辨识框架为｛模型1结果，模型2结果｝，与之对应的BPA值为｛1，0｝；而模型2对应的辨识框架也为｛模型1结果，模型2结果｝，与之对应的BPA值为｛0，1｝。则由式（3）有 K＝1，证据高度冲突，式（3）失效。故而选用式（4）和式（5）对 BPA进行修正。修正后模型 1对应 BPA值为｛0.9901，0.0099｝，模型 2对应的 BPA值为｛0.0099，0.9901｝，则 K＝0.9804，故而由式（3）可得融合后的辨识框架｛模型1结果，模型2结果｝对应BPA值为｛0.5，0.5｝。这很合理，当两个结果均无法彼此否定对方时，得到相同的BPA值。然后由式（7）可以看出，按照第1种方案算出来的结果本质上是对多个结果取平均值。

（2）第2种方案 第1种方案中直接将选用的模型视为正确，忽略了模型之间本身可信度不同的问题，故而第2种方案中引入专家意见。在告知专家案情、所能获取痕迹和计划选用的模型后，邀请不同专家对模型进行评分，对所得分数进行归一化后，将所得结果视为专家对相应模型结果的BPA赋值。专家评分汇总表如表2所示。表中S表示分值，第一个下标为专家代号，第2个下标为模型代号。

表2 专家评分汇总表

由表2可得与之对应BPA赋值，即

然后再用式（3）对证据进行融合，并用式（7）获得最终结果。

4 案例分析

该案例为文献［43］中的案例。某天，一人驾驶小型轿车沿某城市道路由北向南行驶至某匝道处时，与另一人驾驶横穿道路的电动摩托车相撞，造成骑车人受伤、两车不同程度损坏。文献［43］中采用了4种方法计算事故车辆车速，分别为车速预估法、DLT法、仿真法和EDR方法，所得结果如表3所示。

表3 不同模型所得结果 km／h

选择第1种方案时，依据式（3）～式（5）计算后可知辨识框架｛模型1，模型2，模型3，模型4｝所对应的 BPA为｛0.25，0.25，0.25，0.25｝，则由式（7）可得G＝65.2 km／h。这本质上依然是取各模型结果的平均值。

选择第2种方案时，邀请公安部交通管理科学研究所和同济大学等领域内资深专家评分，结果见表4。用式（8）可获得相应的BPA矩阵，见表5。然后先将专家1与2证据融合，可算出K＝0.737，则辨识框架｛模型1，模型2，模型3，模型4｝对应BPA为｛0.096，0.26，0.219，0.425｝；再将此结果与专家 3结果融合，K＝0.733，则辨识框架｛模型 1，模型 2，模型 3，模型 4｝对应 BPA为｛0.071，0.282，0.185，0.462｝。从最终结果可以看出，专家们对EDR所得结果最为肯定。然后由式（7）可得G＝64.8 km／h。

表4 案例中专家评分汇总表

虽然最终两种方案结果只相差0.4 km／h，这是在当前技术水平下完全可以忽略的误差。但不能否认的是，方案2因引入专家意见，故比方案1的结果说服力更强。

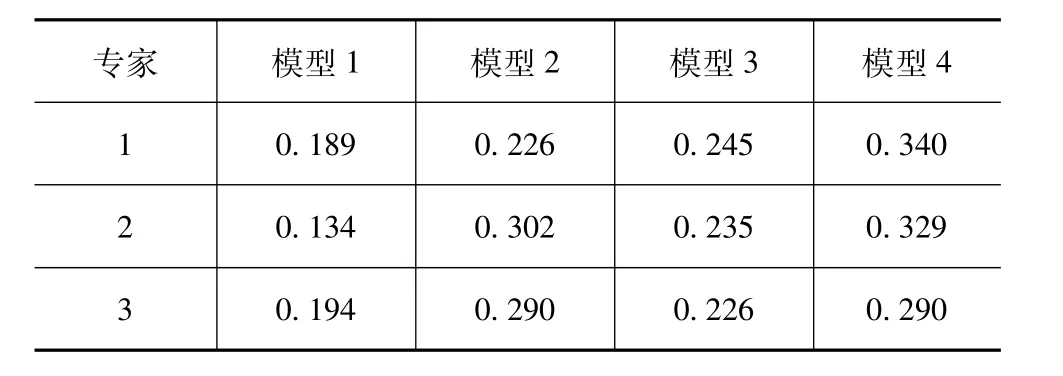
表5 BPA矩阵

5 讨论

上面的案例并未考虑痕迹的不确定性。根据相关专家的意见，考虑痕迹不确定性后，得到的4个模型的区间结果如表6所示。

表6 考虑痕迹不确定性的4个模型所得区间结果km／h

具体可参照文献［9］、文献［31］～文献［33］中的不确定性分析技术依据不确定痕迹计算而得，具体计算步骤从略。此时可采用如下步骤融合结果。

步骤1 先依据各结果区间上下界值大小关系排序，然后组成对应的新区间以获得结果的辨识框架。如该案例中各结果的上下界排序为｛59，63，64，65，66，69，75｝，故而结果的辨识框架为｛［59，63］，［63，64］，［64，65］，［65，66］，［66，69］，［69，75］｝。

步骤2 依据上节中方案确定与各模型结果所对应的 BPA值（如本案例中的｛0.071，0.282，0.185，0.462｝），然后分模型将所得 BPA值按照式（9）分配给结果辨识框架内的焦元，并将不同模型所赋予焦元的BPA值求和作为该焦元的最终BPA值。假定模型所得结果区间［a，b］之BPA值为m，则结果辨识框架内的焦元［c，d］的BPA可用下式计算：

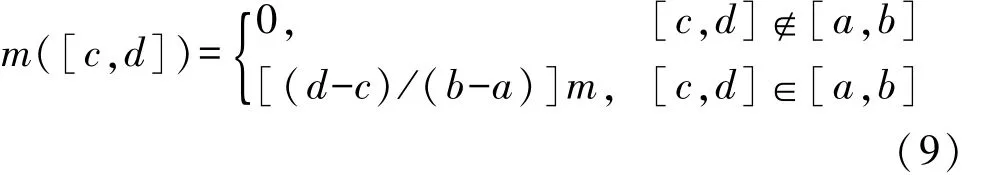
本案例中，经过变换后的BPA赋值矩阵见表7。

由表7可给出最终结果为与辨识框架｛［59，63］，［63，64］，［64，65］，［65，66］，［66，69］，［69，75］｝对应的 BPA值 ｛0.074，0.16，0.391，0.257，0.077，0.043｝。用图的形式表示更为直观，结果见图1。

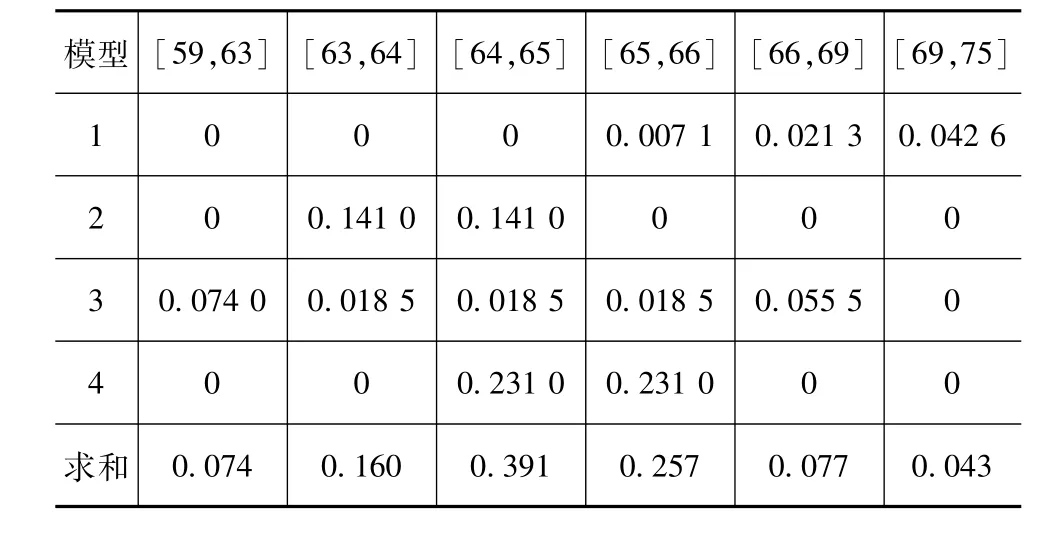
表7 变换后的BPA赋值矩阵

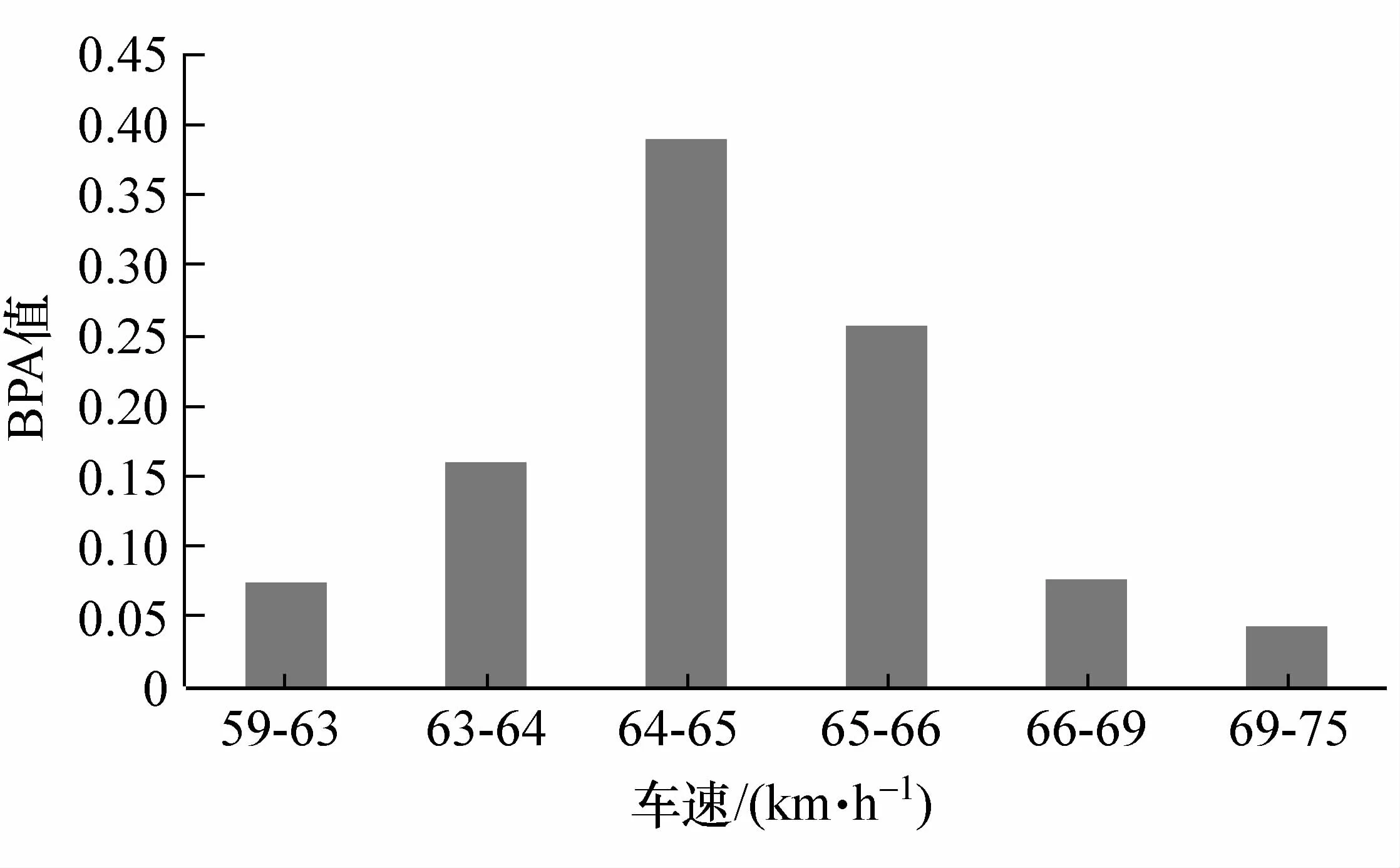
图1 融合结果

由图1可以看出，虽然所给出的结果形式上依然复杂，但相比于简单地取区间［59，75］km／h，图1所示结果显然更为客观，包含的信息也更多。

6 结论

本研究中给出一种基于证据理论的融合方法，为提升事故再现结果客观性提供支持，通过分析得到如下结论。

（1）无论事故再现模型结果是数值还是区间，均可通过证据理论进行融合。融合的关键在于对模型结果基本概率分配的赋值，第1种方案本质上是求取各个结果的均值，而第2种方案则因引入了专家意见而增强结果的可信度。

（2）当证据间（模型结果）高度冲突时，可选用式（4）和式（5）变换后求解，分析发现该方案具有合理性。但是否有更科学的方案依然值得后续研究。

（3）当事故再现模型结果为区间时，可依据步骤对结果进行融合，融合后的结果依然复杂但可读信息更多。

但对事故多模型结果的描述，尚有不足之处。事故多模型结果的不同描述方法孰优孰劣、是否有更合理的方法等未做深入讨论。此外，如何处理高冲突证据、更科学的专家评分方案和区间结果如何更科学地融合等还须做更深入的研究。