人工蜂群算法在空间定位的研究

摘要：在发声目标的定位监测中，空间的坐标位置和发声时刻均为未知，而确定这些因素也是空间定位监测的关键所在。文中提出改进型人工蜂群算法来实现空间定位功能，以便有效地确定空间发声点位置和发声时间。该算法利用快速群体搜索特性，解决算法后期搜索效率低下以及对初始值敏感的缺陷，减小了误差且提高了计算精度。实验结果表明，改进型人工蜂群算法在实际空间定位中既精确又稳定，并能有效提高定位的准确性，具有较高的应用价值。

关键词：空间发声目标;空间定位;人工蜂群算法;搜索效率;计算精度;定位监测

中图分类号：TN911-34; TP301.6

文献标识码：A

文章编号：1004-373X（ 2019）24-0176-04

本文提出一种改进型人工蜂群算法，以实现空间定位。在硬件相同的条件下，只有通过改进定位算法便可将定位系统的精度提升，而定位算法的有效性、可靠性和计算速度成为影响定位效果的重要指标“，。综合考虑，需提出合适的空间定位算法，才能精确定位空间中的声源目标。

1 改进型人工蜂群算法研究

1.1 建立空间定位模型

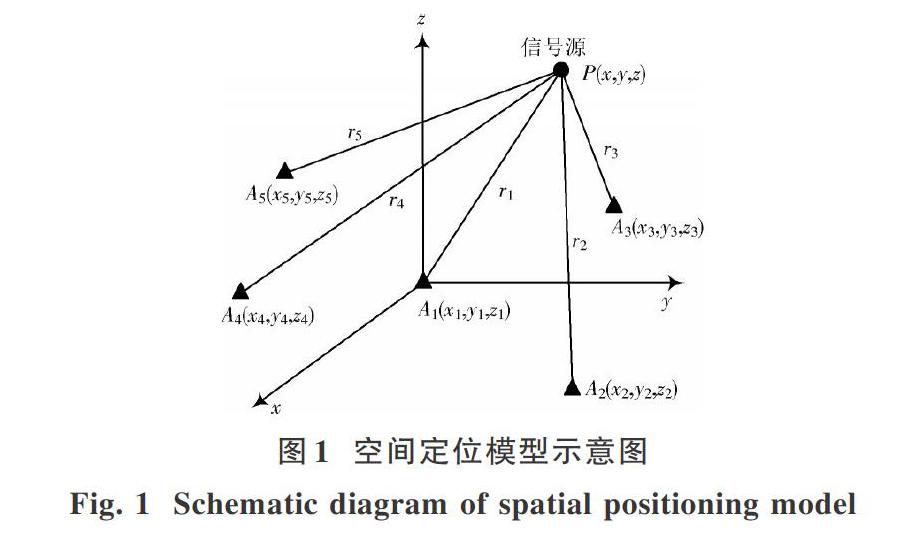
空间定位计算模型就是利用已知各个观测点的坐标，根据这些观测点采集到的盗采行为产生的声波（P波）信号和信号到达观测点的时间，对目标位置进行计算估计从而确定目标位置及目标位置发出信号的时刻。在空间中以一定的方式布置一定数量的传感器，组成传感器阵列，当空间中出现发声事件时，传感器拾取信号，利用多点同步采集每个传感器接收到声波的时刻，联合每个传感器坐标与声波到达时刻代入方程组中求解，从而得到空间中发声坐标参数和时间参数，达到空间定位的目的。在定位计算中，需确定的未知量有5个，其中3个分别是目标位置的（x，y，z）坐标，剩下1个则是目标位置发出信号的时刻t，v一个是声波速度。采用5个或以上的观测点来对目标位置定位。式中，v是声波速度。可看出式（1）中有5个未知数，建立5个方程组，所以是完全闭合的方程组，联立求解便可得到未知数的具体数值。

利用第5个传感器的监测结果，满足第5个传感器列出的方程的解就是所要求解的空间中的发声位置与发声时刻。

1.2 改进型人工蜂群算法定位

利用人工蜂群优化算法与牛顿迭代算法各自的优点，本文提出改进型人工蜂群算法。改进型人工蜂群算法的原理是在人工蜂群运算过程中对每个蜜蜂的适应度评价过程中所产生的更新值代入牛顿迭代算法进行精确计算，之后选择有效方程组解成为蜜蜂新的个体适应值与位置，并与历史最优适应值和位置比较，选出最优值将其当作Pbest并存储。

把当前所有Pbest和Gbest的值作为比较，以便更新Gbest。若适应值误差小于适应值误差容限或迭代次数大过最大迭代次数，则返回全局最优个体Pg，若人工蜂群运算满足终止条件，得出当前结果作为改进型人工蜂群算法所求问题的最优解。

具体实现步骤如下：

1）首先利用上文中建立的实验模型随机初始化蜜蜂的速度和位置;

3）将得出的更新值代人牛顿迭代算法进行精确计算。利用下列步骤进行牛顿迭代计算，同时利用5组空间传感器的数据整合，将各个组合中的数据均代入方程中相应的声波传感器坐标与测到的达到时刻中，得出：

最后选择有效方程组的解成为蜜蜂新的个体适应值和坐标，之后与最优适应值和位置相互比较，选出最优值更新并存储。

4）将所有Pbest和Gbest的值做比较更新Gbest;

5）若满足停止条件，则返回全局最优个体Pg，否则转到步骤2）;

6）若达到停止条件则结束，输出结果就是最优解。

通过上述方式求出空间中发声的位置（xs，ys，zs），实现了改进型人工蜂群算法在空间定位中的功能。采用改进型人工蜂群算法可有效解决空间中的声源定位问题，不易困入局部最优，而无法找到全局最优解。混合算法收敛速度快，确保运算收敛性和收敛速度，定位运算效率优良。

2 空间定位事件验证及分析

2.1 计算机实现算法

根据在空间定位实验室中采集到的传感器数据来进行算法的仿真，具体数据如表1所示。

表1是实验中5个传感器的相对坐标（x，y，z）和采集到的声波到达时间t。

算法设置人工蜂群的种群大小为66，设定人工蜂群一共迭代35次，w惯性权重取1.2，vmax蜜蜂更新速率取0.3，学习因子Ci和C2均取0.8，将传感器采集到的声波到达时间和各传感器的空间位置等数据提供给改进型人工蜂群算法进行运算。由上文提出改进型人工蜂群算法过程进行仿真，从而得出空间位置，仿真计算得到的位置为（3 289，5 024，-765），结果如图2所示。

图2中蓝点表示每一代得出的Gbest位置，改进型人工蜂群算法将每一代速度分量由被重组的蜜蜂值进行调控，之后算出新的蜜蜂位置。在多维蜂群搜索空间中蜜蜂不断改变其自身的状态，从图中看出Gbest蜜蜂向一个小范围逐渐集中，直到得出最优状态或达到计算限制为止，最终得出圆点表示空间中发声源的位置。

2.2 算法空间定位结果分析

实验中声波传感器的坐标和采集到的声波到达时间t，如表1所示。将其代入几种常用的空间定位算法中进行运算。通过对比常用算法计算结果与实地测量之间误差，验证算法的准确性。

根据声波空间定位实验室现场测量得坐标为（2 231，3 054，32）。通过声波传感器测到的数据分别代入Newton、人工蜂群、拟牛顿和改进型人工蜂群算法进行运算，结果如表2所示。

传统Newton迭代要计算n个函数值、雅克比矩阵、求导与求逆，计算量过大，另外对初值依赖过高易出现不收敛，在应用中会带来较大的问题[2-3]。PSO算法后期存在搜索精度较低、易发散等缺點，缺乏局部精细搜索，且后期会出现收敛停滞[4-7]，影响其定位精度。

拟牛顿迭代每一步的迭代方向是沿着当前点函数值下降的方向，克服传统牛顿迭代要求导和求逆的缺点，有较好的全局收敛性和超线性收敛性[8]，但该算法有效性严重依赖于初始点的选择，不利于全局精确搜索。

由于改进型人工蜂群算法在每代蜜蜂的适应度评价过程中产生新值均被代到牛顿迭代进行精确优化，使得每一代产生的Gbest值更精确，从而引导蜜蜂群向声源坐标进行精确稳定地搜索，最终得出的计算结果与实际测量的爆破中心值的误差为△x≈2 m，△y ≈1m，△z≈1m。由此可见，改进型人工蜂群算法计算的空间发声位置是准确的。

3 结语

本文利用人工蜂群算法和牛顿迭代的优点，提出改进型人工蜂群算法。算法将牛顿迭代运算整合到蜂群算法的全局快速搜索运算中，从而实现空间中声源定位。同时利用实际实验，进一步证明该方法的空间定位精度。该算法有效解决了常规的迭代算法对初始值的选择敏感的缺点，另外算法具有较好的全局优化搜索能力及局部精确搜索能力。因此，利用改进型人工蜂群算法能有效获取声源空间坐标位置，故该方法对空间声源定位具有一定的应用价值。

参考文献

[1]王振涛，郝忠孝，贺洪江.基于传声器阵列的声源定位系统的研究[J]华北电力大学学报（自然科学版），2009，36（5）：103-105.

WANG Zhentao. HAO Zhongxiao， HE Hongjiang. Study on au-ditory localization svstem based on microphone array[J]. Jour-nal of North China Electric Power University（Natural scienceedition）， 2009， 36（5）： 103-105.

[2]范卓立，黄根春，基于传声器阵列的声源定位算法与误差分析[J]传感器与微系统，2014， 33 （10）：108-110.

FAN Zhuoli， HUANG Genchun. Sound source localization algo-rithms and error anahsis based on microphone array [J]. Trans-ducer and microsystem technologies， 2014. 33（ 10）： 108-110.

[3]刘云武，杨卫.基于传声器阵列的声源定位系统设计[J]。压电与声光，2014. 36（2）：314-316.

LIU Yunwu. YANG Wei. Design of sound source localizationsystem based on microphone array [J]. Piezoelectrics &acous-tooptics. 2014. 36（2）： 314-316.

[4]陈志敏，薄煜明，吴盘龙，等，基于自适应粒子群优化的新型粒子滤波在目标跟踪中的应用[J]控制与决策，2013.28（2）：193-200.

CHEN Zhimin. BO Yuming， WU Panlong， et al.Novel parti-cle filter algorithm based on adaptive particle swarm optimiza-tion and its application to radar target tracking [J]. Control anddecision-making. 2013， 28（2）：193-200.

[5]武忠勇，缑锦，赵志强，具有白适应邻域探测机制的改进型PSO算法[J]，小型微型计算机系统，2010， 31（9）：1838-1845.

WU Zhongyong， GOU Jin， ZHAO Zhiqiang. Improved particleswarm optimization based on self - adaptive neighborhood ex-plored [J]. Journal of Chinese mini - micro computer systems，2010. 31（9）：1838-1845.

[6]任子晖，王坚.加速收敛的粒子群优化算法[J]控制与决策，2011， 26（2）：201-206.

REN Zihui， WANG Jian. Accelerate convergence particleswarm optimization algorithm [J]. Control and decision， 2011，26（2）：201-206.

[7]孙向军，赵斯强，严宗睿.基于粒子群优化的反潜搜索研究[J]微电子学与计算机，2008.25（10）：91-93.

SUN Xiangjun， ZHAO Siqiang， YAN Zongrui. Antisubmarinesearch research on the optimization of particle swarm[J]. Micro-electronics and computer， 2008， 25（ 10）： 91-93.

[8]张继伟.修正Brovden族拟牛顿算法及其应用[D].长沙：湖南大学，2006.

ZHANG Jiwei. Modified Broyden quasi-Newton algorithm andits application [D]. Changsha： Hunan University， 2006.

[9]何寧，晁建刚，许振瑛，等.增强现实航天飞行训练系统空间定位[J]航天医学与医学T程.2018（2）：255-260.

HE Ning， CHAO Jiangang， XU Zhenying， et al.Research onspatial orientation of augmented reality space flight training sys-tem [J]. Space medicine&medical engineering， 2018（2）： 255-260.

[10]李江.钢箱拱肋安装及空间定位控制研究[J]交通世界，2018 （7）：90-91.

LI Jiang. Study on installation and space positioning control ofsteel box arch rib [J]. Transpo world. 2018（7）： 90-91.

作者简介：霍桂利（1968-），女，河北邢台人，硕士，副教授，研究方向为数学及计算机科学与应用。