热损失型风速传感器流体动力学分析与实验研究

李东升 刘清惓 孙星 吕鸣晨

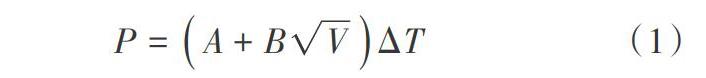
摘要：为解决传统机械式风速计难以准确测量低风速的难题，设计一种热损失型风速传感器。该传感器主要由Cor-tex-M3 ARM处理器、高精度低噪声测量电路及恒功率加热电路等组成。通过计算流体动力学（CFD）方法确定探头加热功率，并得到双探头温度差值与风速的曲线关系。搭建一套基于高低温试验箱的实验平台，对-10-50℃范围内的传感器温度特性进行测试，结合L-M算法对温漂进行修正。实验结果表明，在0-5 m/s范围内，该风速传感器的均方根误差（RMSE）为0.09 m/s，在低风速测量领域具有一定的应用潜力。

关键词：风速传感器;探头温差计算;低风速测量;温漂修正;算法拟合;仿真验证

中图分类号：TN64-34

文献标识码：A

文章编号：1004-373X（2019）24-0011-05

0 引言

风速测量在航空航天、工农业生产、环境监测以及空调、新风系统等领域有着广泛的应用[1]。在气象领域，气象站主要使用机械风杯式风速计来测量风速，其量程较大且价格相对较低;但其存在启动风速大、难以准确测量0.5 m/s以下风速和机械磨损导致测量误差增大等局限翻。超声波式风速传感器可实现0.01 m/s量级的分辨率，但声波在传播过程中幅度衰减较大，易受噪声、阴影效应、雨雪天气等因素的影响[3]，且高精度超声波风速传感器价格昂贵。热式风速计凭借尺寸小、低风速下测量灵敏度高等特点，在气象、工业领域对低风速测量具有应用潜力[4]。

由于环境温度的变化将导致气流以及传感器元件的物理特性发生改变，因此温漂对热式风速传感器的测量精度有显著影响[5]。文献[6]使用人工神经网络算法对标定数据进行训练并修正温漂影响，最终测量数据的均方根误差为0.098 m/s。在标定和测试时，其环境温度变化范围仅为15-30℃，温漂修正范围有限。文献[7]提出一种通过测量功率差计算风速的传感器，在风速为0-5 m/s时，最大误差小于+0.25 m/s，但其并未对温漂影响进行分析和修正。

为进一步降低热式风速计温漂影响并提高测量精度，本文提出一种热损失型热式风速传感器，主要包括恒功率加热探头、环境温度探头、高精度测量电路，并提出一种利用L-M算法修正温漂的方法，对-10-50℃范围内温漂影响进行误差修正。

1 热损失型风速传感器设计

本文提出一种热损失型风速传感器，工作时，由加热元件提供热量，通过测温元件测量流体流动引起的热量变化来反应风速大小。由于热损失型风速传感器在工作过程中同时存在热传导和热对流两种传热形式，结合流体薄层边界层理论，可得到半经验公式为：

P= （A+ B√V）△T

（1）式中：P为加热探头加热总功率;A和B为常量，由传感器尺寸、材料特性和流体性质决定;V为流体流速;△T为加热探头与环境温度的差值。

本文提出的热损失型风速传感器测量示意图如图1所示，测量装置主要包括加热探头、环境温度探头、低热导率支撑杆及基座。结合式（1）可知，采用恒功率加热方式时，通过测量双探头的温度差值△T即可计算出风速。此外，测量时两个探头需保持一定距离以保证环境温度探头与加热探头之间没有热量传递。

2 计算流体动力学仿真分析

2.1 物理模型建立

本文采用ProE软件建立仿真模型，双探头结构图如图2所示。其中，加热探头包含测温铂电阻、导热铝片及四个加热电阻;相比于加热探头，环境温度探头没有加热电阻。为增加受热铂电阻与风的对流换热，提高低风速测量灵敏度，本文采用加热电阻放置在导热铝片下方的结构。为使导热均匀，设定铝片为圆形结构并将铂电阻置于铝片上表面中心位置，加热电阻置于铝片下表面且对称分布。

建模时，按实物尺寸将加热电阻尺寸设为3.5 mmX1.8 mmx0.6 mm，铂电阻尺寸为2 mmx2 mmX0.5 mm;铝片直径设为12 mm，厚度为0.2 mm。加热电阻中心点到铝片圆心距离设为3.7 mm。

2.2 网格划分

本文采用网格划分软件ICEM对模型进行适应性较强的非结构化四面体网格划分。本文空气域尺寸为100 mmX100 mmx250 mm。由于探头尺寸小，空气域较大，因此对探头的网格划分使用了局部加密，确保仿真的精度。最后，经网格质量检验，网格质量大于0.3，可认为网格质量良好，满足FLUENT求解要求[8]。

2.3 计算流体动力学仿真分析

本文选用计算流体动力学（ CFD）软件FLUENT对传感器模型进行流固耦合分析，以求解在不同加热功率和风速条件下的温度场。求解时采用压力传感器进行定常流动计算。本文模型涉及对流换热及热传导，故需开启能量方程。根据雷诺系数计算，本文采用湍流模型，K-epsilon标准模型。压力和速度耦合采用SIMPLE算法，求解先采用一阶迎风格式，再采用二阶迎风格式。空气域入口边界条件采用速度入口，出口边界条件采用压力出口。

加热探头的功率过高会增加系统功耗，在低风速下探头升温过高亦会加速元器件老化，但加热功率过小又会降低传感器的灵敏度。恒功率加热模式下，加热探头升温约60 K时，可兼顾功耗和灵敏度指标。在仿真中，将加热功率分别设为0.3 W，0.5 W，0.8 W以及1W，对不同风速条件进行仿真。仿真结果表明，加热功率为0.5 W时，低风速下升温接近60 K，因此选择0.5 W作为该传感器的加热功率。环境温度为300 K，风速分别为0.2 m/s和1 m/s时，加热探头温度场如图3所示。风速为0.2 m/s时，加热探头最高温度可达348 K;风速为1 m/s时，加热探头最高温度降为321 K。可见风速对加热探头的温度场分布影响显著。

為进一步探讨在不同风速情况下双探头温度差值和风速的曲线关系，对0.1-5 m/s范围内进行仿真，得到双探头温度差值和风速的关系图，如图4仿真曲线所示。双探头温度差值与风速呈单调递减关系，在低风速时曲线斜率较大，温差变化明显;随着风速的升高曲线斜率趋缓。

3 硬件電路设计

硬件电路系统框图如图5所示，主要包括Cortex-M3内核的微处理器STM32F103、高精度模拟信号采集电路、恒功率加热控制电路及电源电路等部分。

为提高精度，采用A级铂电阻PTlOO作为热敏元件，并采用四线制接线法，消除导线电阻的影响;使用Isotech的镓固定点和Fluke的水三相点和电压噪声低至3 nV的Fluke1595A测温电桥对铂电阻进行标定。为提高分辨率和测量的线性度，采用24位∑一△低噪声模/数转换芯片AD7794对模拟信号进行转换。为进一步降低噪声、减少模拟测量端的漂移，采用噪声1.2μV，温漂系数+3 PPM/℃的外部基准源ADR444为ADC提供基准电压;采用精度为±0.01%、温漂系数为+5 PPM/℃的精密电阻作为测量和加热电路参考电阻。最终铂电阻温度测量精度可达0.02℃。

恒功率加热电路由精密参考电阻、低温漂精密加热电阻、光电耦合器4N25以及功率开关组成。为更好实现对设定功率的控制，充分考虑加热电阻在长期使用过程中产生的阻值漂移，本文采用基于增量式PID控制算法和脉宽调制技术PWM进行恒功率加热控制[9]。控制算法中，通过模/数转换芯片AD7794采集加热电路并联参考电阻和串联参考电阻的有效电压，利用Cortex-M3处理器对采集的电压进行防脉冲干扰平均值滤波处理，再计算出实时加热功率。通过PID算法计算实时功率P与设定功率Pset的偏差值AP，结合脉宽调制技术输出相应占空比的PWM波。实验结果证明，在比例系数KP=20.5，积分系数K1=8.5，微分系数KD=0.2时，加热功率可稳定在0.494-0.508 W之间。

在PCB设计过程中，将数字地与模拟地分开，并使用0 Ω电阻单点耦合数字地与模拟地，从而降低高频数字信号对模拟信号的干扰。电路的实物图如图6所示。

4 实验平台搭建及测试

为验证CFD仿真的准确性并研究热损失型风速计的温漂影响，本文搭建了一套基于高低温试验箱的风速检测模拟实验装置，装置结构图和实物图如图7所示。该装置主要由高低温试验箱、数据采集与发送系统、直流减速电机控制系统以及旋转机械结构组成。

本文采用高低温试验箱改变测量环境温度，该实验箱温度工作范围为-60-120℃。数据采集模块及主控系统板置于旋转电机上方，加热探头与环境温度探头分别置于支撑板的两端，支撑板采用低热导率材料以降低加热探头与电机的热量传递。该平台通过采集直流电机旋转的角速度，结合探头距直流电机的水平中心距离，采用探头线速度模拟风速。

实验时，首先设定环境温度为27℃，采集不同风速情况下双探头的温度差值，得到双探头温度差值与风速的关系曲线如图4实测曲线所示。由图可知，实测曲线与仿真曲线趋势相同。改变试验箱温度设定，分别测量环境温度为-10℃，0℃，10℃，20℃，30℃，40℃，50℃时，不同风速情况下双探头的温度差值并绘制温度差值与环境温度的关系曲线，如图8所示。

由图8可知，当风速一定时，随着环境温度的升高，温差值会有所增加。当风速大于2 m/s时，由于不同风速条件对应的温差值较为接近，温漂造成的误差对风速测量结果的影响尤为显著，为提高测量精度需对温漂进行修正。

5 算法拟合与分析

5.1 基于L-M算法的公式拟合

L-M算法是一种非线性最小二乘法[10-11]，是高斯一牛顿法和梯度下降法的结合，具有高斯一牛顿法的局部收敛性和梯度下降法的全局特性。本文采用L-M算法对标定得到的数据进行公式拟合，得到风速V、环境温度死及双探头的温度差值△T三者的函数关系式v=f（T0，△T）。将拟合公式存入代码中，即可输出经温漂修正后的测量值。

5.2 实验分析

为验证传感器的性能及温漂修正效果，采集12组数据进行验证，结果如表1所示。由表1可知，采用L-M算法拟合后，在环境温度为-10-50℃范围内，风速测量的均方根误差（RMSE）为0.09 m/s;风速在0-2 m/s和2-5 m/s范围时，最大测量误差分别为+0.08 m/s和+0.14 m/s。可见，经温漂修正后，该风速计对低风速的测量精度较高，且适用环境温度范围广。

6 结语

本文针对低风速难以准确测量的难题，设计了一种热损失型双探头热式风速传感器，具有结构简易、温漂修正范围广、低风速测量精度高等特点。测量电路采用铂电阻结合24位∑一△低噪声模/数转换器提高测量精度，并采用L-M算法对温漂进行修正。实验结果表明，该风速计在-10-50℃工作环境下测量的均方根误差为0.09 m/s，风速在0-2 m/s和2-5 m/s范围时，最大测量误差分别为+0.08 m/s和+0.14 m/s。该风速计在气象测量领域可作为机械风杯式风速计的补充，弥补其无法准确测量低风速的不足，同时在空调通风等领域也具有一定的应用潜力。目前本文仅针对温漂影响进行了修正，在后续的研究中将考虑空气湿度、气压等因素的影响，进一步提

高测量进度。

[1] LAGHROUCHE M， ADANE A. BOUSSEY J. et al. A minia-ture silicon hot wire sensor for automatic wind speed measure-ments [J]. Renewable energy ， 2005 ， 30（ 12） ： 1881-1896.

[2] DONG Z Q， CHEN J J，QIN Y K， et al.Fabrication of a micro-machined two-dimensional wind sensor by au-au wafer bondingtechnology [J]. IEEE journal of micro - electromechanical svs-tems， 2012， 21（2）：467-475.

[3] ZHU W J，XU K J，FANG M. et al.Mathematical modeling ofultrasonic gas flow meter based on experimental data in threesteps [J]. IEEE transactions on instrumentation and measure-ment， 2016. 65（8）：1726-1738.

[4] ZHU Y Q， CHEN B， GAO D. et al.A robust and low-power 2～D thermal wind sensor based on a glass-in-silicon reflow pro-cess [J]. Microsystem technologies， 2016. 22（1）： 151-162.

[5] HUANG Q A， CHEN B，ZHU Y Q， et al.Modeling of Tem-perature effects on micro-machined silicon thermal wind sen-sors [J]. IEEE journal of micro - electromechanical systems，2015， 24（6）： 2033-2038.

[6] BOUSSAD Idjeri， MOURAD Laghrouche， JUMANA Boussey.Wind measurement based on mems micro - anemometer withhigh accuracy using ANN technique [J]. IEEE sensors journal，2017.

17（ 13）： 4181-4188.

[7] WANG S，YI Z X， QIN M， et al.A 2D wind sensor using thedelta P thermal feedback control [J]. Journal of micro-electrome-chanical systems， 2018. 27（3）：377-379.

[8]張凯.Fluent技术基础与应用实例[M].北京：清华大学出版社，2010.

ZHANG Kai. Fluent technology foundation and application ex-amples [M]. Beijing： Tsinghua University Press， 2010.

[9]张唏，曾迪晖，王永立，基于STM32的的无刷直流电机控制系统[J]仪表技术与传感器，2013（9）：31-33.

ZHANG Xi， ZENG Dihui. WANG Yongli. Brushless DC motorcontrol svstem based on STM32 [J]. Instrument technique andsensor. 2013（9）： 31-33.

[10]史忠植.神经网络[M].北京：高等教育出版社，2009.

SHI Zhongzhi. Neural networks [M]. Beijing： Higher Educa-tion Press. 2009.

[11]盛洪江，毛建东，李学生，等，基于Levenberg-Marquardt算法的直流电感器电感参量估计[J]电力自动化设备，2016， 36（5）：171-175.

SHENG Hongjiang， MAO Jiandong， LI Xuesheng， et al.In-ductance parameter estimation of DC inductors based on lev-enberg - marquardt algorithm [J]. Automatic power conversionequipment， 2016. 36（5）： 171-175.

作者简介：李东升（1992-），男，硕士研究生，主要研究方向为传感器技术及应用。

刘清倦（1979-），男，教授，博士生导师，主要研究方向为MEMS传感器技术、气象探测。

孙星（1995-），男，硕士研究生，主要研究方向为传感器技术及应用。