一种基于System Generator的CORDIC算法实现

胡天翔 陈科 赵志强

摘  要：在现场可编程门阵列（FPGA）芯片的应用中，选择坐标旋转数字计算（CORDIC）算法来实现正余弦函数的实时计算有着广泛的应用。同时在信号处理领域上，对正余弦函数的计算有着高精度的需求。据此采用Simulink平台的Xilinx公司开发工具System Genenrator（SysGen）设计了基于CORDIC算法实现正余弦函数计算的FPGA模型，将角度计算范围扩展到全实数领域，并在理论上推导出该设计方案计算结果的误差上限。仿真结果显示，该设计方案的误差精度与理论推导保持一致。而且，相比SysGen的系统自带模块，该设计可以避免重复尝试，更好地控制计算精度。

关键词：坐标旋转数字计算机;现场可编程门阵列;正余弦函数;计算精度;System Generator

中图分类号：TN911.72      文献标志码：A         文章编号：2095-2945（2020）19-0023-06

Abstract： In the application of field programmable gate array （FPGA） chip， choosing the Coordinate Rotation Digital Computer （CORDIC） algorithm to realize the real-time calculation of sine and cosine functions has a wide range of applications. At the same time， in the field of signal processing， there is a demand for high precision in the calculation of sine and cosine functions. Based on this， the FPGA model of sine and cosine function calculation based on CORDIC algorithm is designed by using System Genenrator （SysGen）， a development tool of Xilinx company on Simulink platform， which extends the range of angle calculation to the field of all real numbers， and deduces the upper limit of error of the calculation result of the design scheme in theory. The simulation results show that the error accuracy of the design scheme is consistent with the theoretical derivation. Moreover， compared with the system with its own module of SysGen， this design can avoid repeated attempts and better control the calculation accuracy.

Keywords： coordinate rotation digital computer; field programmable gate array; sine and cosine functions; calculation accuracy; System Generator

引言

在AI、自動驾驶及物联网等信息技术蓬勃发展的今天，数据处理的高精度实时性需求越发被人们所重视。在现场可编程门阵列（FPGA）出现伊始，业界就有一种观点认为FPGA可以被用来加速计算（computing）的过程。现今FPGA更是已经成为数字信号处理系统的核心器件，其高速并行能力使得它成为高性能数字信号处理的理想平台[1]。

传统的FPGA设计流程，需要从算法设计阶段的高层次计算机语言（如C++）转换到硬件实现阶段的底层HDL语言（如Verilog），这个过程的时间成本很高，而且易产生一些错误[2]。MATLAB中的Simulink给复杂的DSP算法的硬件化提供了一个很便利的开发平台，在该平台上，利用Xilinx公司的开发工具System Generator（SysGen）不仅可以快速准确的实现硬件的建模与仿真，而且可以将抽象的模块化电路图直接转化为硬件描述语言，并生成测试文件，可以有效缩短开发周期[3]。

传统的CORDIC（Coordinate Rotation Digital Computer）算法在圆周坐标系统下的的收敛范围在[-99.82°，99.82°]，并没有覆盖到任意角度[4]。且CORDIC算法具有迭代性，迭代次数和定点数运算中数据位宽的选择都直接关联到计算结果的精度。增加迭代次数和数据位宽都会带来硬件资源占用的影响，同时反复进行迭代也会使得运算速度变慢。这样在满足工程上精度需求的前提下，合适地选择迭代次数和数据位宽可以在节省硬件资源成本和响应速度上得到很好的兼顾。

针对上述问题，为避免设计时的不断重复尝试。本文在Simulink平台上针对圆周系统下CORDIC算法设计了正弦余弦函数的计算模块，将可计算的范围扩展到任意角度，并在理论上给出了该设计的误差上限。根据本文给出的误差上限分析，适当选取迭代次数和数据路径中的小数位数，可以同时兼顾计算速度和硬件消耗，更高效地实现定点数的正余弦函数计算。

1 CORDIC算法基本原理

CORDIC算法由J.Voider等人于1959年在航空控制系统的设计中提出来[4]。这种算法应用于硬件平台上，只要执行移位和加法运算，就能实现一些复杂的超越函数（如三角函数）。该算法在数字信号处理领域得到了广泛的应用。其算法原理如下[5]。

在CORDIC算法圆周坐标系旋转中，给定的初始向量{x（0），y（0）}，起始角度z（0）。第i次迭代旋转如图1所示。

3 基于System Generator的CORDIC正余弦计算模块设计

FPGA厂商Xilinx公司在Simulink平台上提供了System Generator开发工具，用户可以基于此工具高效建模，在FPGA上实现DSP算法。还可以自动生成HDL代码和测试文件，将模型直接转化为ISE工程，大大提高了设计效率[7]，是数字信号处理系统设计与Xilinx公司FPGA实现的“桥梁”。而且在SysGen环境下，采用基于模型的设计方法可以方便地实现和验证定点算法，发现问题后也容易进行修改[8]。

3.1 模块设计方案

本次模块针对正弦和余弦计算，采用的是CORDIC算法圆周坐标系下的旋转模式。设置初始向量为？淄（0）=（1/Kn，0）'，同时z（0）为我们要求解的目标角度。经过n次迭代后迭代累计角度z（n）趋近于0，也就意味着向量旋转趋近于目标角度。此时的向量模长增益趋近于1，向量的x坐标趋近于cosz（0），y坐标趋近于sinz（0），据此可计算z（0）的正弦值和余弦值。

由于传统CORDIC算法的覆盖范围有限，为了将计算角度扩展到[-∞，+∞]，我们需要对初始计算角度进行旋转。第一、四象限角度位于CORDIC收敛范围之内，将第二、三象限角旋转至第一、四象限中与其正弦值相同的角度。这样就将角度映射至CORDIC的收敛范围之内，此时余弦值为正，将其赋值为负即为原角度的余弦值。模块整体结构如图2所示。

计算角度的映射和余弦符号修正两个模块采用SysGen中的MCode模块来实现。该模块使用M语言来描述Verilog要表述的逻辑[9]，我们可以将逻辑控制按照MCode要求的语法写入.m文件，进而装载到MCode模块中。这样我们就将.m文件转化为SysGen的一个组件，可以无缝结合到整体模型的构建中。

对输入的任意角度（度），需要将其转到0～360°范围内的角度，采用求余的方式达成。进而加入MCode完成角度映射功能，将角度映射到[-90°，+90°]。角度映射模块的MCode嵌入代码如下所示：

function z = quadrant_trans（x）

if 0 <= x && x < 90

z = x;

elseif 90 <= x && x < 270

z = 180 - x;

else

z = x - 360;

end

如果計算角度属于第二、三象限，余弦符号修正模块产生逻辑值1，否则逻辑值为0，将逻辑值输入到选择器中。如果为第二、三象限角，选择器输出迭代模块产生x值的非。余弦符号修正模块的MCode嵌入代码如下所示：

function z = cos_modify（x）

if 90 <= x && x < 270

z = xfix（{xlBoolean}， 1）;

else

z = xfix（{xlBoolean}， 0）;

end

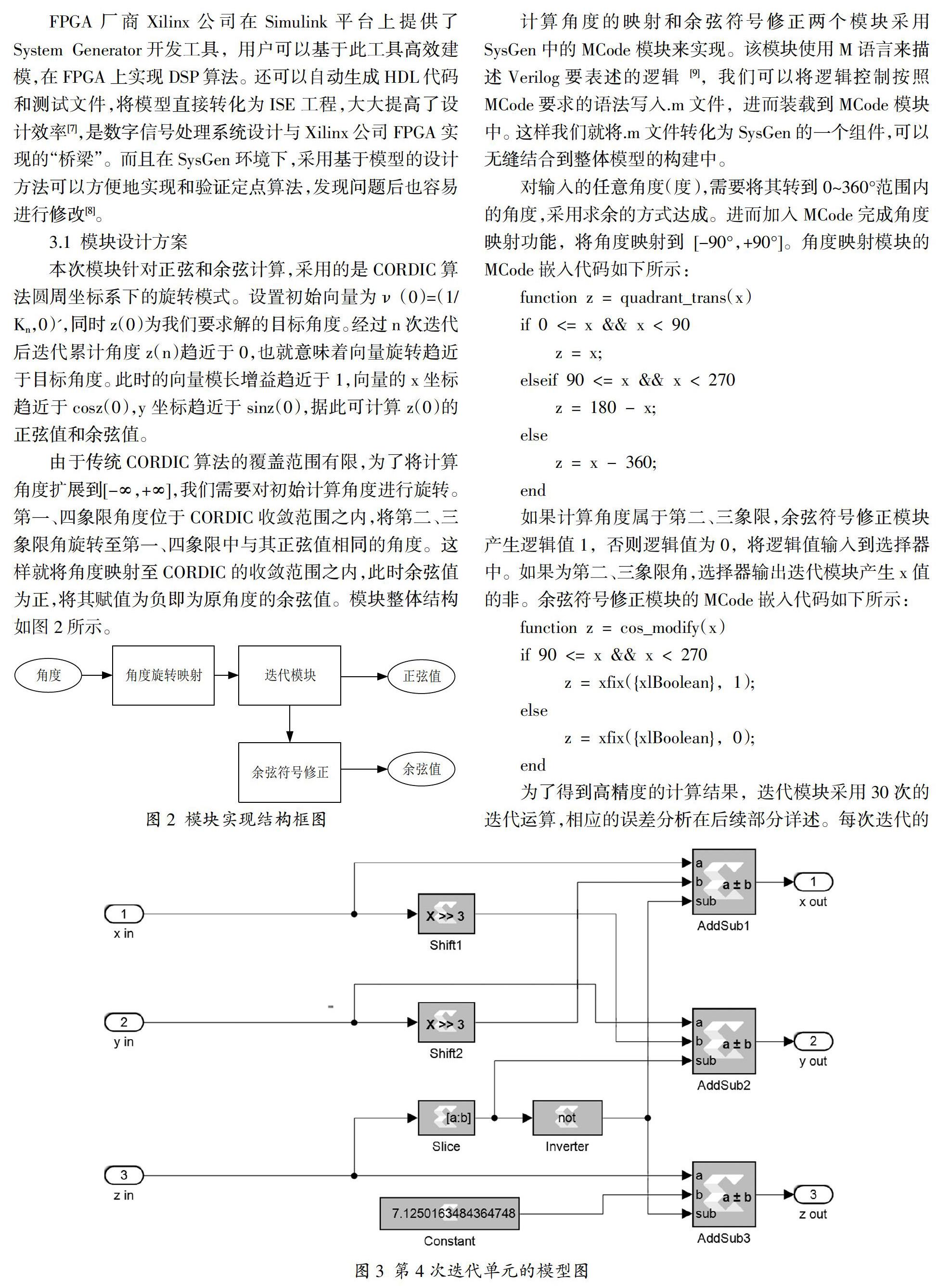
系统整体模型如图4所示，如前所述，输入常量x为1/K（30），K（30）为伪旋转30次迭代后所产生的增量倍数，输入常量y为0。Mod_function为取余运算模块，将全范围的角度转到[0°，+360°]范围内。经30次迭代运算后，输出y为正弦值，输出x经多路选择器输出后为余弦值。

3.2 模块整体误差分析

4 仿真结果与分析

在[-1000°，1000°]内随机生成20个角度值带入设计的模块中做正弦值计算。将所计算的结果与MATLAB代码计算的结果做差求得误差集合。以横坐标为角度（以度为单位），纵坐标为误差值作图，正弦计算误差曲线如图6所示，余弦计算误差曲线如图7所示。

从以上两图可以看到，随机生成的角度经设计模块运算后的的正余弦值计算结果误差均未超过4.1665×10-8，与我们理论分析的结果是一致的。

将System Generator自带模块，设置同样的迭代次数和位数，对20个随机生成的角度进行求解，所得结果与MATLAB计算结果的误差曲线图如图8所示。本文所设计的正余弦函数计算模块的精度要优于系统自带模块。