不锈钢芯板材料结构网格划分方法


摘 要:基于传统有限元网格划分方法无法计算出不锈钢芯板计算理论值的情况下,通过对不锈钢芯板试验模型在三点弯曲工况下的有限元模型计算研究,了解不同的几何简化方法及网格尺寸对计算结果的影响,提出了一套可靠的网格划分方法。研究结果表明:传统有限元网格划分方法刚度计算结果失真,网格细化后的应力计算结果不收敛,采用新型不锈钢芯板网格划分方法可以使计算结果收敛,根据收敛曲线,可以选取最少的节点划分数量获得较为准确的结算结果,因此新的不锈钢芯板材料网格划分方法可以有效解决当前工程实际计算问题。
关键词:不锈钢芯板;有限元;网格划分;计算精度
1 引言
不锈钢芯板(后面简称为芯板)是一种新型夹层结构,由面板和芯管组成,其芯管由薄壁圆管按照一定间距排列组成,面板和芯管翻边应用铜钎焊焊接.不锈钢芯板虽然由简单的几何形体构成,但是形成了复杂的结构整体,在采用有限元离散网格划分时,会产生数量庞大的离散网格单元,在计算机性能的限制下,往往不得不对有限元模型进行各种程度的简化。目前在国内已知的研究当中,大部分研究人员采用的是与舒兴平[1]等前沿研究学者相同的网格划分方法,作为传统的网格划分方法,比较适合理论分析,但是与试验结果有时会产生较大差距,为了解决这些问题,需要研究一种更贴近真实的兼顾计算精度和计算效率的芯板网格划分方法。
2 有限元网格划分
随着有限元软件在国内的大量实际运用,越来越多的企业及产品方案开始采用有限元软件进行力学性能的计算分析,在使用有限元软件分析时,如何才能得到准确的计算结果,这是一个很关键的问题。
有限元计算结果的准确性,很大程度上是由网格的划分来决定的,网格越小,计算结果越精准,网格越大,计算效率越高,通过张俊[2]等人的研究证明,可以通过研究结构网格尺寸和计算结果的变化,来观察计算结果是否收敛,而开始收敛的临界尺寸大小,就是能达到较高计算精度的最高效网格尺寸。
计算效率也是选择网格尺寸的时候需要考虑的问题,较小的网格可以让计算结果收敛,但是计算量本身可能已经超过了计算机的承受极限。宋少云[3]等人的研究证明了网格划分中遵从力学里面的圣维南原理[4],“如果物体一局部边界表面所承受的表面力是一平衡力系,这个平衡表面力只在受力附近产生显著的应力,而在远处其应力可略去不计”,因此为了获得精确的计算结果,可以在局部对网格进行细化加密。
模型的几何清理简化对有限元计算结果的影响也是非常巨大的,根据李融林[5]等人的理论,如果存在尖角,“就算在奇点附近加密剖分,计算结果的收敛效果依然不能令人满意”,所以在模型的简化中,需要注意尖角对计算结果的影响。
为了研究不同网格全局尺寸参数及模型简化策略对计算结果的影响,采用HyperMesh软件提供的强大手动网格划分工具,对芯板划分高质量的四边形结构化网格单元,并通过对芯板三点弯曲试验模型实例的有限元分析,对芯板模型从几何简化方式,网格单元尺寸等方向进行全面的研究。
3 芯板算例模型
为了研究上述网格划分的理论,建立图1所示的芯板结构(B0.4-40芯板)三点弯曲试验模型,芯板尺寸1219 mm×350 mm,中心施载区域101.6 mm ×350 mm,载荷大小为317 N的垂向集中力,试验跨距为1016mm,一端支座约束3个方向移动自由度,另一端支座约束芯板横向和垂向移动自由度。对芯板进行网格划分。
4 芯板几何简化
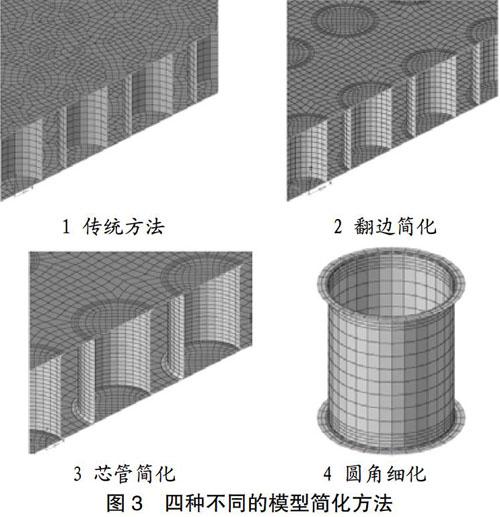
为了研究传统模型几何简化方法对计算结果分析的影响,针对芯板的翻边。建立了全局尺寸为4mm的四种细化程度依次增加的有限元模型,四种网格模型的划分效果见图3。
传统网格划分方法:芯管简化为圆柱片体,与面板直角交接,网格采用Abaqus进阶算法划分,导入HyperMesh软件施加载荷约束并提交计算。
翻边简化法:在传统网格划分方法的基础上,在面板几何上按翻边外径切割,并对切割的翻边几何赋予真实的料厚属性。
芯管细化法:对芯管完整几何进行独立的网格划分,并用一排单元模拟芯管圆角,芯管翻边和面板之间添加钎焊实体单元。
芯管圆角细化法:考虑到尖角奇点[5]的问题,在芯管细化法的基础上,对芯管圆角进一步细化,体现为网格经线尺寸为全局尺寸,纬线尺寸为圆角几何尺寸四等分划分,并对圆角附近的纬线均加密至一定水平。
四种不同的模型简化方法计算结果对比效果见表1。
从表1的相对误差可以看出,在应力计算方面,圆角细化法的计算精度要比前面几种都要高,具体原因在后文作详细介绍。在位移计算方面,传统方法位移比后三种均增大了33%左右,存在较大的误差,后三种方法计算结果偏差在0.2%以内,从计算效率上来看,翻边简化法仅用了圆角细化法52%的节点数就得到了相同的计算结果,是当前分析案例模型最优的几何简化法。
5 芯板网格尺寸
有限元网格划分的基本步骤是,通过确定全局网格尺寸,对选定区域进行自动划分,然后手动调节网格质量,在实际分析中,第一步需要确定合适的全局网格尺寸,才能保证所有的计算工作最终产生的是真实的理论解。为了找出适合于芯板材料分析的全局网格尺寸,借鉴张俊[2]等人关于网格尺寸收敛性的研究方法,对芯板案例模型在不同全局网格尺寸下的位移及应力分析计算结果进行研究,找出合适的网格单元尺寸。
5.1 刚度计算
刚度计算主要是考察结构在作用力下的最大位移量。在对芯板案例模型进行网格划分时,分别选择全局网格尺寸在12~1之间的一系列数值,網格划分方法采用上文论证过的翻边简化法,得到共7个有限元模型用于计算。芯板案例有限元模型的刚度计算结果见图4。
从图4可以看出,当网格尺寸越小,位移值越大,从4mm开始,后面的计算结果偏差均小于1%,计算结果趋于收敛,所以选取4mm的全局网格尺寸,可以很好的平衡模型计算效率和计算精度。
5.2 应力计算
应力计算主要是考察结构在作用力下全局节点反馈的最大应力值。首先,需要确保模型能得到正确的刚度计算结果,根据上文的分析结论,全局网格划分方法采用尺寸为4mm的翻边简化法。根据圣维南原理[4]。仅需对应力最大的单一芯管进行应力研究,对该芯管网格划分的时候,采用上文论证过的芯管圆角细化法,为了追求更高的计算精度,需要借鉴郭晓霞[6]等人关于四边形单元二分法的研究,对芯管应力最大区域进一步局部加密,以研究计算结果的收敛性。
有限元四边形网格是由经线和纬线合围而成的结构化网格单元,为了进一步减小网格加密的计算量,需要进一步研究网格经线和纬线方向上加密分别对计算结果收敛性产生的影响。
经线加密是让芯管直径圆弧更贴合真实圆形。由于模型的全局基本尺寸是4mm所以,由4~2~1mm依次对经线间距进行(应力最大区)局部加密。
纬线加密是让芯管根部圆角更贴合真实曲面。由于芯管应力最大区在圆角附近,所以依次对圆角进行1~5排单元的局部加密,并且依照加密后的纬线间距,对局部圆角周边应力较大区域内的网格,按圆角同尺寸间距值进行加密,并逐渐过渡至全局网格尺寸。
计算结果如下:
从图5可以看出,当网格经线间距越小,应力计算结果几乎没有改变,也就是说当前网格尺寸已经使计算结果趋于收敛。
从图6可以看出,当网格纬线间距越小,应力计算结果逐渐收敛,此案例中芯管圆角为R0.5mm,划分为4排网格则宽度仅0.18mm,模型节点数量仅增加了2.5%,所以选取0.18mm的局部圆角网格尺寸,可以很好的平衡模型计算效率和计算精度。
6 芯板网格划分方法
通过研究几何模型简化,网格尺寸大小对有限元计算结果的影响,总结上文的网格划分思路,得出一套研究应力位移真实理论值的芯板高精度网格划分方法:
1)对模型进行几何简化,在面板几何上切割出翻边的区域,然后进行布种及网格划分。2)通过对网格模型的研究建立位移收敛曲线图,选取最高效的网格全局尺寸搭建有限元模型。3)完成刚度分析,得出位移真实理论值。4)通过刚度分析,找出应力最大点,通过对芯管局部网格细化加密的研究,获得应力收敛曲线图,并选取最高效的圆角网格尺寸搭建局部有限元模型。5)完成应力分析,得出应力真实理论值。
7 结论
采用新的不锈鋼芯板网格划分方法得到的有限元模型,可以对芯板材料构成的产品进行准确的力学性能研究。刚度计算结果比传统网格划分方法提高了33%,应力计算结果比传统网格划分方法提高了37%。
参考文献:
[1]舒兴平,彭妍,刘泽龙.不锈钢芯板梁受弯性能有限元分析[J].湖南科技大学学报(自然科学版),2019,34(01):36-411.
[2]张俊.有限元网格划分和收敛性(1)[J].CAD/CAM与制造业信息化,2010(04):99-103.
[3]宋少云,尹芳.有限元网格划分中的圣维南原理及其应用[J].机械设计与制造,2012,37(09):63-65.
[4]徐芝伦.弹性力学[M].北京:高等教育出版社,1992.
[5]李融林,倪光正,俞集辉.极坐标系中的B样条有限元法在求解尖角奇异边值问题中的应用[J].计算物理,1997,14(01):121-127.
[6]郭晓霞.四边形有限元网格划分方法-二分法的改进[J].塑性工程学报,2005,12(05):96-100.
作者简介:皮子丰(1988-),男,湖南长沙人,本科,车身工程师,从事芯板材料车身应用方向研究。

