可延展电子通用金属互连结构电学特性分析
王文惠 潘开林 龚似明 范凯
摘要:为探究可延展通用互连结构的不同几何参数和拉伸率在高频条件下对电学性能的影响,利用有限元法对通用互连结构金属导线的电感与拉伸率和频率之间的变化关系进行研究。利用正交试验对通用互连结构的几何参数、拉伸率和频率对交流电感的影响进行了分析。结果表明,等效圆弧半径、等效水平线段、厚度以及斜线段是对导线交流电感的主要影响因素,为可延展通用互连结构的设计和优化提供了参考依据。
关键词:互连结构;电学特性分析;正交试验;交流电感;金属导线;仿真分析
中图分类号:TN98-34;0342;0343.1
文献标识码:A
文章编号:1004-373X(2019)24-0059-04
0 引言
传统的电子产品受到材料本身刚性和脆性等特点的限制,使其应用范围受到一定限制。而可延展柔性电子克服了传统无机电子脆、硬的特点,使器件实现了弯曲和变形的能力,能够在三维曲面环境中进行工作,在生活中得到了广泛的应用,如表皮的健康监控[1-2]、可延展电池[3]及机器人皮肤[4-5]。
可延展柔性电子按照材料类型可分为可延展柔性有机电子和可延展柔性无机电子。可延展柔性有机电子和可延展柔性无机电子相比,前者因压电系数、介电常数和电子迁移率相对较低,限制了其在高速电子领域的应用,而可延展柔性无机电子能够保持良好的电学性能,因此在高速集成电路中广泛使用。通用型可延展无机金属互连结构可通过结构几何参数的改变,使其结构发生较明显的变化,以适应不同的应用场合。由于其结构的特殊性,几何参数与拉伸率对电学特性的影响至关重要。
现在对于可延展柔性互连电子在电学方面的研究相对较少,其中具有代表性的有:Huang Y等人对岛桥结构的可延展能量存储设备进行研究[6],在0-20%的应变下,经历10万次循环后,仍能够保持良好的电学性能;Wang等人对改良后的喷墨印制电路导线在不同程度的折叠状态下呈现的电学性能进行了研究[7];Dong等人针对三层夹心结构PI- Cu -PI( Polymide - Cu -Poly-mide),马蹄形互连导线变形后在进行了仿真研究,并提出了一种计算其电学特性的仿真流程[8];安刚等人提出了一种新型算法研究了蛇形互连结构在不同应变下的电学特性,并利用实验进行了验证[9]。
以往的研究一般只针对形变对导线和器件产生的影响做出了研究,并未对电学参数产生影响的结构几何参数做出具体分析。由于可延展通用互连结构的特殊性,针对此问题,利用有限元法和正交试验对该结构进行了研究。1建模
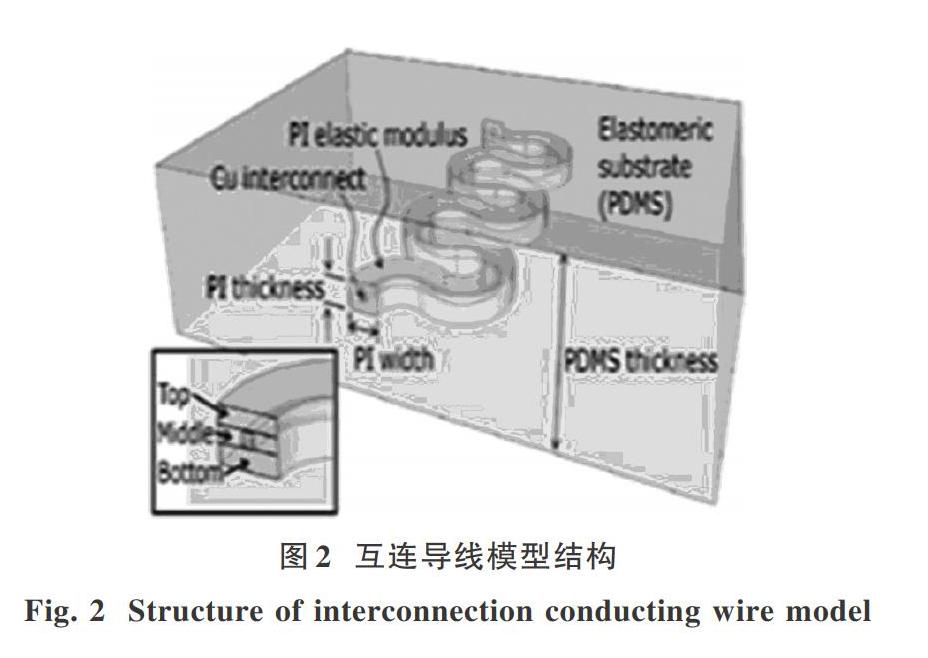
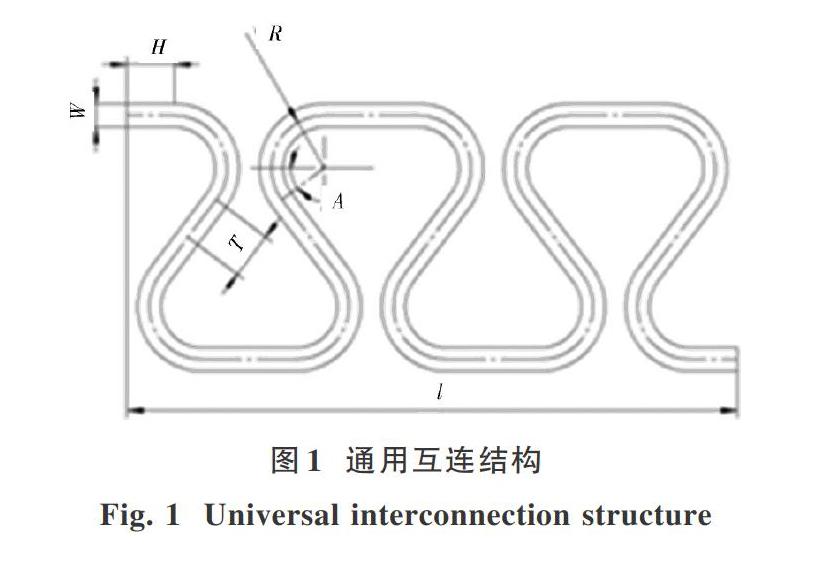
仿真研究模型为可延展通用互连结构[10],如图1所示。平面二维通用互连结构模型有6个结构参数,分别为等效水平线段H、等效圆弧半径R、角度A、等效斜线段T、导线宽度W、等效长度l。。互连金属导线嵌入在PI中,具有一定的厚度tCu,其为PI- Cu-PI三层夹心结构,如图2所示[11],模型尺寸如表1所示。
基于SOLIDWORKS和有限元软件,根据设计数值,建立三维通用互连结构模型。互连导线材料为铜箔,其密度为8.9×103 kg/m3,杨氏模量E=85 GPa,泊松比[12]为0.3。通过对模型的切割,采用四节点平面应力单元(CPS4R)进行扫略网格划分。对通用互连结构有限元模型施加的位移分别为100 μm,120μm,140μm,160 μm,180 μm,200 μm。然后提取形变后的参数,重新构造形变后的模型并导出。
2 仿真结果分析
对初始导线模型给予不同形变,得到不同形变下单根通用互连导线交流电感与频率之间的关系图,如图3所示。由图中可以看出,所有互连导线的交流电感都会随着频率的增加而减小,这与受到的趋肤效应[13]影响有关。由于电感的计算是利用等效方法计算得到,为导线内部与外部电感之和,即L=Lin+Lout。当频率逐渐增加,导线内部磁场最终消失,内部电感也逐渐减小至零,外部电感等效于高频条件下的电感值[14]。在同一频率条件下,互连导线的交流电感会随着互连导线形变的增加而增加,图3中,在频率范围为0-1 GHz条件下,所有形变后的互连导线其交流电感相对与初始值变化较小,最大减小量约5.4%。当频率为固定频率0.5 GHz的条件下,由于互连导线形变量逐渐增大,当达到最大拉伸位移200 μm以后,此状态下的交流电感与初始交流電感之相比较增加了约21 .6%。对比不同频率和拉伸位移对互连导线交流电感变化率的大小,得知通用互连结构形变对交流电感的影响远大于频率。图4显示了频率为0.5 GHz时,不同形变条件下单根通用互连导线的交流电感变化情况。
3 正交试验
为了能比较全面地研究通用互连结构的几何参数、形变以及频率对交流电感的影响,文章利用更简单、直观的正交试验方法。将互连结构中基本的几何参数(水平线段日、半径R、角度A与斜线段T、铜导线的厚度tCu)、拉伸率( Elongation)以及频率,作为探究因素。各因素水平数为3,探究因素为7,如表2所示。不考虑因素间的交互作用,服从正交表列数大于因素个数的选取规则,选用L27( 313 )正交表,其中第1至第7列用于放置探讨的7个影响因素;而第8至第12列为空白列,将所有的空白列作为误差所在列,最后一列为试验指标,填放仿真试验结果,即通用互连导线交流电感ACL,试验数据如表3所示。
3.1 极差分析
对导线的指标ACL进行分析,结果如表4所示。表中K1,K2,K3分别代表各个因素在1,2,3三水平下通用互连结构指标均值,而R代表的是不同因素的极差值。从结果可以看出,各个因素的影响主次顺序为R>H>tCu>T>f>A>Elongation。
3.2 方差分析
虽然极差分析可以确定各因素的主次关系,但是考虑到影响因子改变带来的试验数据差别和误差变动引起的试验数据差别,为保证试验结果的准确性,对试验结果进行方差分析,结果如表5所示。根据方差分析结果可知,在分析的7个影响因素中,半径R、水平线段日、厚度tCu在显著性水平为0.05,置信区间为95%时,P值均不大于0.05,这三个因素对结果的影响较为显著,其他因素对结果影响不显著。这与上述极差分析的结果保持一致。
3.3 交互作用分析
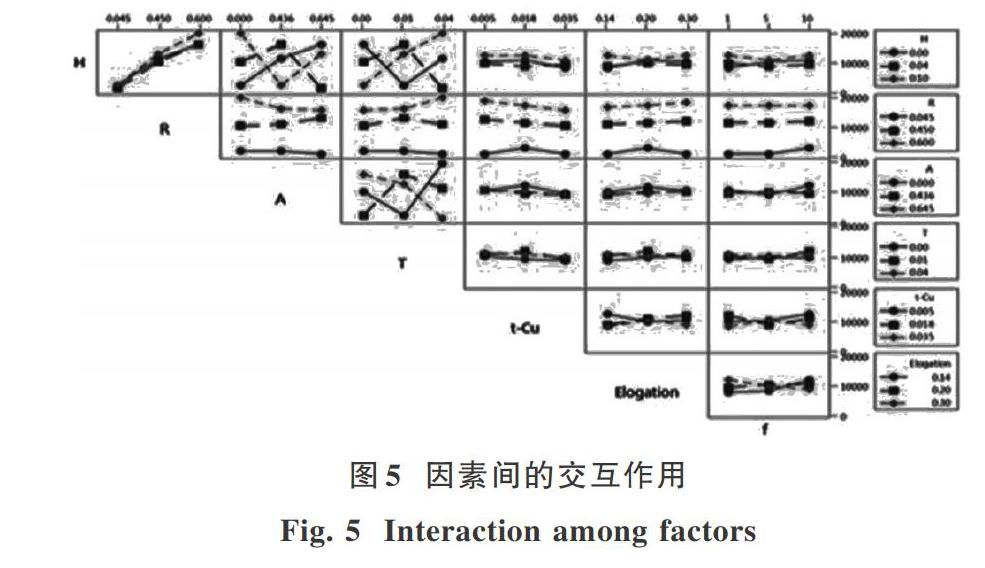
图5给出了探究的各因素之间的交互作用关系。由图5可知,通用互连结构的交流电感不仅受单因素的影响,并且各个因素之间的交互作用也会对其产生影响。从图中可以看出与因素R存在交互作用的因素对指标ACL的影响并不显著。
其他组合的交互作用都相对显著,交互作用AxH,TxH,TxA等对指标ACL的影响表现出强烈的交互作用。因此在對结构进行设计时,还需考虑斜线段T。
4 结论
本文研究了可延展通用互连结构几何因素、拉伸率和频率对电学性能的影响。通过对通用互连结构电感参数进行分析,确定了对其电学特性产生影响的显著性因素。
研究结果表明,拉伸率和频率改变对电感的影响小于结构参数。在进行可延展通用互连结构设计时,需优先考虑互连半径R和水平线段H、厚度tCu,并考虑因斜线T段与水平线段H,R等由于交互作用使导线拐角发生突变产生的影响。在频率高于10 GHz和拉伸率较大的形变条件下,频率和拉伸率改变带来的影响则需要进一步考虑。研究内容为通用互连结构的设计和结构优化提供了一定的参考价值,为信号完整性的分析奠定了基础。
参考文献
[1] TRUNG T Q, LEE N E. Flexible and stretchable physical sen-sor integrated platforms for wearable human-activity monitorin-gand personal healthcare [J]. Advanced materials. 2016, 28 ( 22) : 4338-4372.
[2] ZHENG Y L, DING X R. POON C C Y. et al. Unobtrusivesensing and wearable devices for health informatics [J]. IEEEtransactions on biomedical engineering, 2014. 61 (5) : 1538-1554.
[3] KALTENBRUNNER M. ADAM G. GLOWACKI E D. et al.Flexible high power-per-weight perovskite solar cells with chro-mium oxide-metal contacts for improved stability in air [J]. Na-ture materials . 2015 . 14( 10) : 1032-1039.
[4] LU N, LU C. YANG S. et al. Highly sensitive skin-mountablestrain gauges based entirely on elastomers [J]. Advanced func-tional materials , 2012. 22( 19) : 4044-4050.
[5] MANNSFELD S C, TEE B C, STOLTENBERG R M. et al.Highly sensitive flexible pressure sensors with microstructuredrubber dielectric layers [J]. Nature materials, 2010. 9(10) :859-864.
[6] HUANG Y. TAO J. MENG W, et al. Super-high rate stretch-able polypyrrole -based supercapacitors with excellent cyclingstability [J]. Nano energy, 2015, 11: 518-525.
[7] WANG Y, GUO H. CHEN J. et al. Paper-based inkjet-printedflexihle electronic circuits [J]. ACS applied materials & inter-faces. 2016. 8( 39) : 174-181.
[8] DONG Z, DUAN B. CAO Z. et al. Electromechanical model-ing of stretchahle interconnects [J]. Journal of computationalelectronics, 2017 , 16( 1) : 202-209. 2015.
[9]安刚.可延展柔性互连模型研究[D].西安:西安电子科技大学。2015
AN Gang. Research on extensible flexible Interconnection mod-el [D]. Xi ' an : Xidian University . 2015.
[10]左峰。潘开林。秦睛,等,可延展电子金属导线通用连续构延展展性表征研究[J].机电工程 , 2016 , 33 ( 7) : 888-894.
ZUO Feng, PAN Kailin, Qin Qing, et al. Study on the ductil-ity characterization of the universal interconnection structureof extensihle electronic metal conductors [J]. Mechatronics en-gineering, 2016, 33(7) : 888-894.
[11] HSU Y Y, GONZALEZ M, BOSSUYT F, et al. Polyimide-en-hanced stretchable interconnects: design, fabrication, andcharacterization [J]. IEEE transactions on electron devices,2011. 58( 8) : 2680-2688.
[12] LEE C H. KIM Y J. HONG Y J. et al. Flexible inorganic nanostructure light - emitting diodes fabricated on graphenefilms [J]. Advanced materials , 2011 , 23 ( 40) : 4614.
[13]于争 .信号完整性揭秘 [M].北京 :机械 工业出版社 . 2013.YU Zheng. Signal integrity disclosure [M]. Beijing :
Mechanical Industry Press, 2013.
[14]陈宝君.集成电路互连线电阻电感参数提取方法研究[D].大连 :大连理 工大学 . 2012.
CHEN Baojun. Study on the extraction method of inductanceparameters for interconnect resistance of integrated circuits[Dl. Dalian : Dalian University of Technology, 2012.
作者简介:王文惠(1993-),女,河南新郑人,硕士研究生,从事可延展电子延展性研究工作。
潘开林,男,四川泸州人,博士,教授,从事先进电子制造技术研究工作。
龚似明,男,广西梧州人,硕士研究生,从事可延展电子延展性研究工作。

