余弦定理问题特征对其解法迁移的影响

郭凯路 张令伟 许云尧

(1．首都师范大学数学科学学院 100037；2．石家庄学院理学院050038；3．北京市东城区教育研修学院 100062)

1 问题提出

样例在原理学习与迁移过程中的作用，前人已经做了较多的研究.Gentner提出的类比结构映射理论是源问题与靶问题两种不同情境下的结构和等级关系的映射，其中映射是对共同内在关系的映射[1]．有研究者把样例从表面内容和原理内容两方面对迁移的影响做了较为系统的研究，研究指出样例的表面内容对新手解决问题有重要作用，对熟悉者也有不同程度的影响[2-3].内在原理是问题所包含的内在结构或关系，是解决问题的关键[2]. Gick，Reed以及Holyoak和Koh等人研究指出，样例的表面内容只对提取有影响，应用或者映射过程将不受表面内容的影响，而只是对问题的结构信息敏感[4-6]．

Ross一系列的实验研究以及莫雷、唐雪峰在Ross的研究基础上进一步做出的研究指出，样例的表面内容在类比源的选取和匹配过程都有影响；问题表面概貌的相似可能影响原理的通达，对原理的运用可能没有影响.Ross的一系列的实验研究以大学生为被试，概率原理问题为材料，系列地研究了样例的表面内容对迁移的影响，检验了样例表面内容对迁移的影响；同时研究结果显示对象对应主要影响原理的运用.在他的研究中表面概貌的变化，只限于事件属性方面的变化[7-8].莫雷、唐雪峰以高中一年级学生和大学一年级学生为被试，排列与组合应用题为材料，研究了样例与问题在事件类型方面发生变化时，其不同相似程度的表面概貌对原理运用的影响.结果表明表面概貌在事件类型方面发生变化时，其表面概貌不同相似对原理运用表现出明显的影响[9-10]．

从已有的研究看到，多数样例问题特征的研究涉及的数学学科知识多是概率应用题、排列组合应用题及运动和工程问题等为材料，对问题特征的某一方面变化进行研究，比如莫雷设计的一系列研究限于事件属性方面的变化对迁移的影响，而莫雷、唐雪峰实验是研究样例与问题在事件类型方面发生变化对迁移的影响，张令伟、连四清、许云尧研究样例和测试题在事件属性和事件类型两方面都发生变化时，样例与测试题的不同相似程度对迁移的影响[11].张令伟等人的研究是以示范学校学生为被试，而对于普通校学生为被试时，试题的事件属性和事件类型都发生变化时结果如何，研究的较少.本研究拟采用余弦定理的推导与应用的数学知识为实验材料，以普通学校学生为被试，样例和测试题在事件属性和事件类型两方面都发生变化时，样例与测试题的不同相似程度对迁移的影响.在本实验中，不同事件属性表现为样例的不同呈现方式；不同的事件类型表现为样例的不同知识呈现方式．

2 研究方法

实验设计：本实验采用3(学生类型：学优生，中等生，学困生)×2(知识呈现方式：转化法，向量法)×4(样例呈现方式：解三角形(字母与公式一致)，解三角形(字母与公式不一致)，证明题，应用题)×9(迁移水平：1、2、3、4、5、6、7、8、9)混合实验设计，其中学生类型、知识呈现方式和样例呈现方式为被试间变量，迁移水平为被试内变量.研究变量为迁移成绩.

被试：选择北京市某中学高一年级三个班的学生作为被试，共103名学生.根据期中考试的成绩将学生分为学优生，中等生，学困生三个类型.考虑到余弦定理是高中数学的基础知识，又是初中直角三角形知识的延续，部分学生可能通过课外的学习已经掌握，因此在实验研究之前有一个前测，将已经掌握余弦定理的学生的测试数据在统计分析时剔除.在实验过程中有学生没有按要求进行实验，如测试卷上不写姓名，或成绩非常异常，这些学生被试的测试数据在统计分析时也被剔除，最后有94名学生被试的数据有效.

实验材料：实验材料包括学习材料和测试材料.学习材料作为源问题，含有余弦定理的证明过程，并有例题，其中证明过程按转化法和向量法分成两种，例题按解三角形(字母与公式一致)，解三角形(字母与公式不一致)，证明题，应用题分四类，共八套学习材料.测试材料作为靶问题，由9道测试题组成.题目分为四类，第一类测试题是解三角形(字母与公式一致，与样例相似)，有两道题.第二类测试题是解三角形(字母与公式不一致，与样例相似)，有两道题.第三类测试题是证明题(与样例相似)，有一道题.第四类试题是应用题，共有四道题，第六题与样例相似，但提示了中间步骤，第七题与样例相似，第八题与第九题与样例不相似，两道题本身相似，第八题给出了图形.为了消除题目的顺序影响，本实验的测试材料采用拉丁方设计，共有9套测试卷.在测试材料上给出了余弦定理的两种形式，六个公式.

实验程序：首先让被试学习15分钟学习材料，然后收回学习材料，同时发给被试测试材料，25分钟后统一收回测试材料.

数据处理：每道题满分均为10分.答案完全不正确的记0分；每道题能识别转化成解三角形问题，能正确用公式记5分；答案完全正确记10分.

3 实验结果

对余弦定理的迁移成绩进行描述性统计分析.表1是迁移成绩平均分和标准差的描述性统计结果，其中A1为知识呈现方式为转化法，A2为知识呈现方式为向量法，B1为样例呈现方式为解三角形且字母与公式一致，B2为样例呈现方式为解三角形且字母与公式不一致，B3为样例呈现方式为证明题，B4为样例呈现方式为应用题.

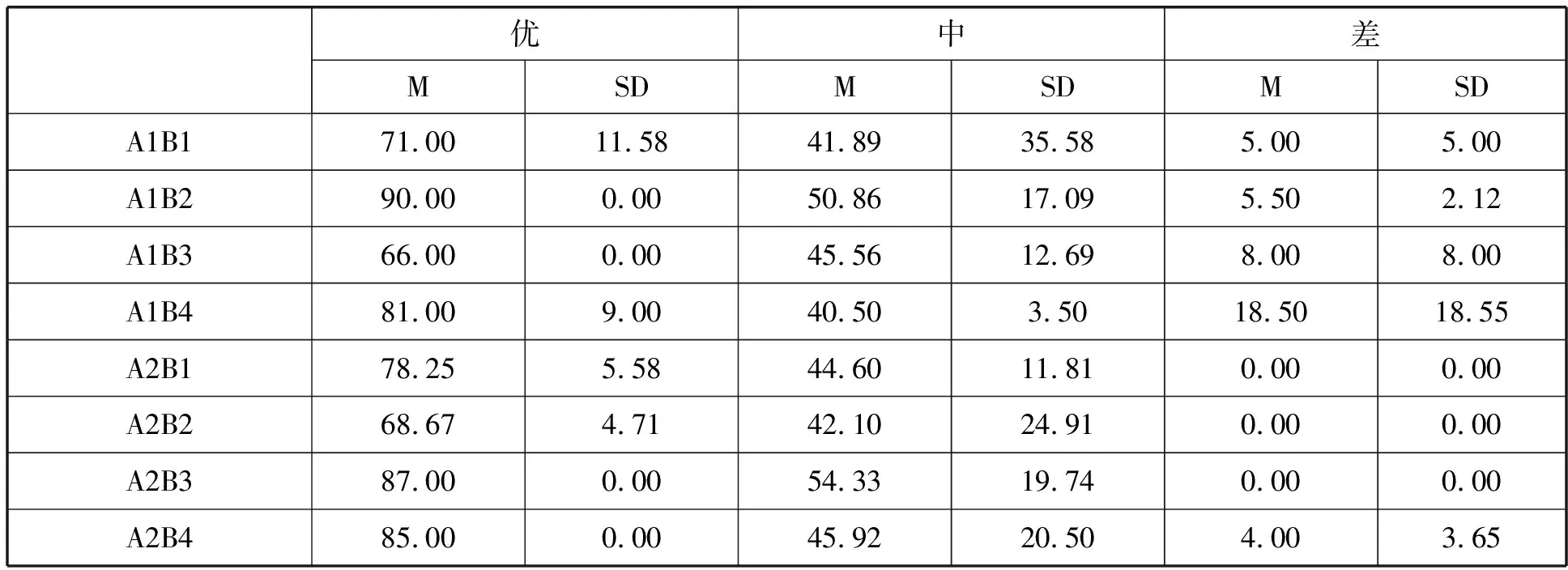
表1 普通高中余弦定理问题解决类比迁移成绩描述统计表

从表1可以看出，知识呈现方式对学优生，中等生影响不显著，而对于学困生则有一定的影响，转化法明显优于向量法.样例呈现方式对各类学生均有一定的影响，对于学优生，学习材料为转化法时，样例呈现方式为解三角形且字母与公式不一致时成绩最好；对于中等生，学习材料为向量法时，样例呈现方式为证明题时成绩最好；而对于学困生，学习材料为转化法时，样例呈现方式为应用题时成绩最好.

对余弦定理的迁移成绩进行3×2×4×9重复测量方差统计，其中学生类型、知识呈现方式和样例呈现方式为被试间变量，迁移水平为被试内变量.统计结果如表2和表3.

表2是普通高中余弦定理类比迁移成绩的重复测量方差分析表，被试内效果检验结果表明：迁移水平的主效应显著(F=3.816，P=0.000).这说明迁移成绩在9个迁移水平上存在显著差异.其中，不同迁移水平的迁移成绩的均值大小顺序为：迁移水平5>迁移水平2>迁移水平3>迁移水平1>迁移水平4>迁移水平9>迁移水平6>迁移水平8>迁移水平7.

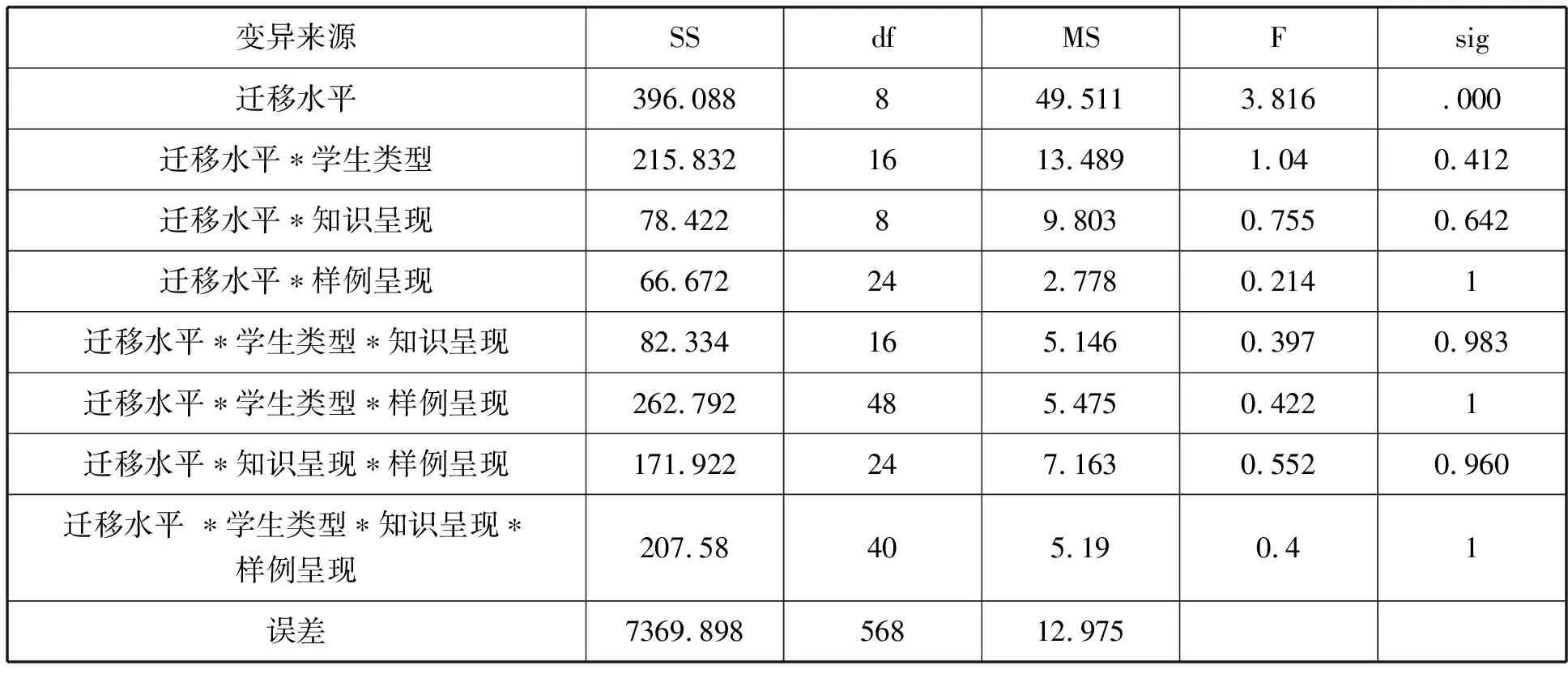
表2 被试内因素主效应方差分析结果

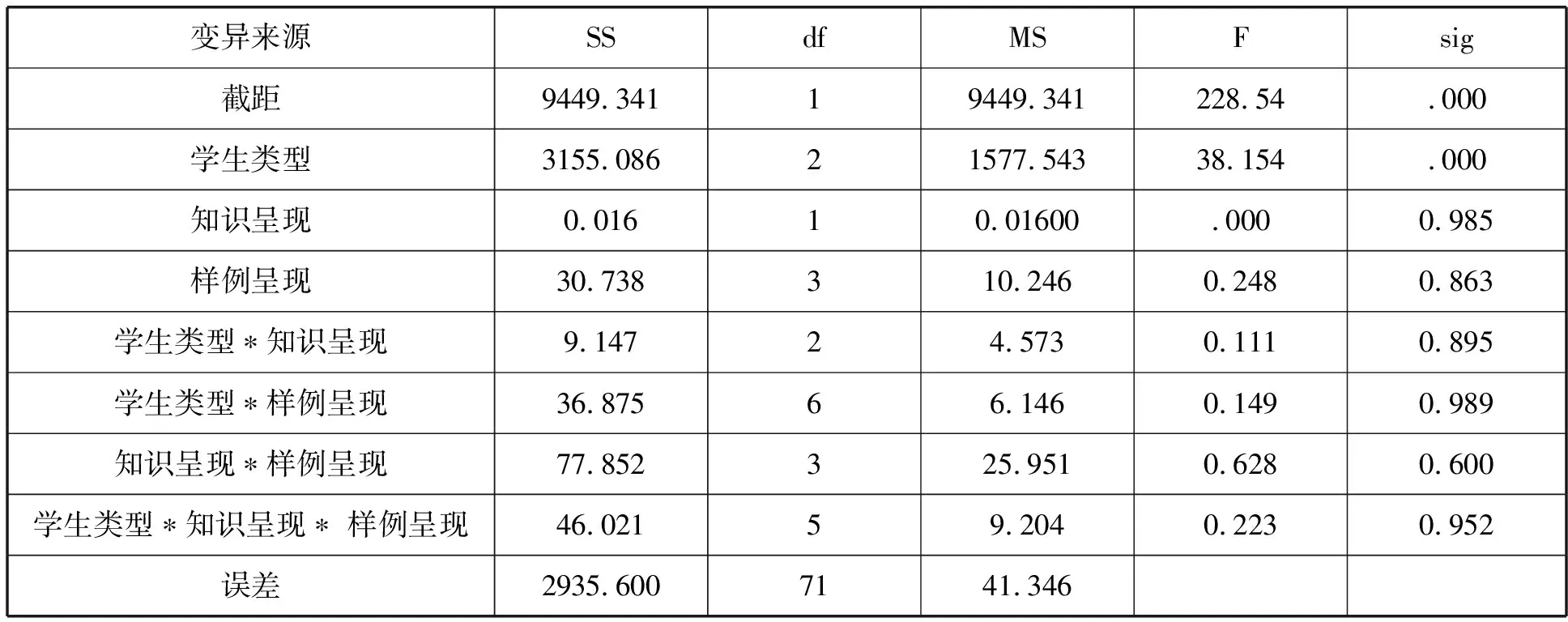
表3 普通高中类比迁移成绩方差分析表(被试间效果检验)

迁移水平与学生类型交互作用不显著(F=1.04，P=0.412).这说明迁移水平在学生类型三水平上不存在显著差异.迁移水平与知识呈现方式交互作用不显著(F=0.755，P=0.642).这说明迁移水平在知识呈现方式两水平上不存在显著差异.迁移水平与样例呈现方式交互作用不显著(F=0.214，P=1).这说明迁移水平在样例呈现方式的四个水平上不存在显著差异.迁移水平 、学生类型与知识呈现方式交互作用不显著(F=0.397，P=0.983).这说明迁移水平与知识呈现方式交互作用不存在学生类型上的显著差异.迁移水平、学生类型与样例呈现方式交互作用不显著(F=0.422，P=1).这说明迁移水平与样例呈现交互作用不存在学生类型上的差异.迁移水平、知识呈现方式与样例呈现方式交互作用不显著(F=0.552，P=0.960).这说明知识呈现与样例呈现交互作用不存在迁移水平的差异.迁移水平、学生类型、知识呈现方式与样例呈现方式交互作用不显著(F=0.400，P=1).这说明迁移水平、知识呈现与样例呈现交互作用不存在学生类型上的差异.

表3是普通高中余弦定理类比迁移成绩的重复测量方差分析表，被试间效果检验结果表明：学生类型的主效应显著(F=38.154，P=.000).这说明余弦定理的迁移成绩在学生类型三水平上存在显著差异.多重均值比较结果显示：学优生与中等生的差异显著(P=.000)，学优生与学困生的差异显著(P=.000)，中等生与学困生的差异也显著(P=.000).

知识呈现的主效应不显著(F=.000，P=0.985)，这说明余弦定理的迁移成绩在知识呈现方式上不存在显著差异.样例呈现方式的主效应不显著(F=0.248，P=0.863)，这说明余弦定理的迁移成绩在样例呈现方式上不存在显著差异.

学生类型与知识呈现方式的交互作用不显著(F=0.111，P=0.895)，这说明知识呈现方式的主效应不存在学生类型上的差异.学生类型与样例呈现方式的交互作用不显著(F=0.149，P=0.989)，这说明样例呈现方式的主效应不存在学生类型上的差异.知识呈现方式与样例呈现方式的交互作用不显著(F=0.628，P=0.600).这说明样例呈现方式的主效应不存在知识呈现方式上的差异.学生类型、知识呈现方式与样例呈现方式的交互作用不显著(F=0.223，P=0.952)，这说明知识呈现方式与样例呈现方式的交互作用不存在学生类型上的差异.

4 分析与讨论

本研究的目的是了解普通高中学生类比迁移能力的现状，探讨普通高中不同类型的学生(没有经验的新手)作为被试时，在余弦定理问题解决中，样例与测试题的问题特征相似性对问题解决的类比迁移成绩的影响.实验的基本设想是：迁移水平、样例呈现和知识呈现特征对问题解决的迁移成绩都有影响，而且三个特征的不同相似性对不同类型的学生影响也会不同.

4.1 被试内因素效应分析与讨论

实验被试内因素效应的结果表明：迁移水平对于普通校学生主效应十分显著.普通学校的实验中迁移水平因素对迁移成绩影响十分显著，这一结果与我们的预期基本一致.结果说明，对于普通校的学生来说，测试题的不同水平影响问题解决方法的通达、提取和应用.其原因可能是：被试通过对余弦公式推导以及样例学习，进一步通过样例和测试题表面特征的比较，可能已经概括出或者部分概括出样例与测试题在不同水平下它们之间所蕴涵的关系和结构，进而在解题过程中直接把这种关系和结构映射过来.如在实验中，水平1和水平2的测试题与样例的表面概貌相似，表面对应也相似(在两实验中都属于第一类测试题)，学生几乎都可以把样例的解法迁移到测试题中；而实验的第二、三类测试题都是与样例表面概貌、表面对应部分相似，被试不易揭露隐蔽在具体变化情节中的关系和结构，迁移过程不如第一类测试题进行的顺利.实验中的第四类测试题属于表面概貌和表面对应都不完全相似的类型，比如实验中的测试题8：“在四边形ABCD中，已知AB=3，AD=5，BC=4，DC=4，A=60°，求cosC”与四套测试题的样例表面概貌都不相似，在一定程度上结构相似.在测试题8的解题过程中两次应用余弦定理，学生不能揭示这种隐蔽的条件，使得迁移顺利完成.对于不同水平测试题所蕴含的关系和结构不同，且与样例的表面特征存在具体情节上不同变化，使得学生可能不能揭露各种隐蔽条件，看出测试题与样例表面特征的隐蔽的相似性，从而在问题解决过程中迁移不一定能顺利完成[10].

对于普通校的学生来说，迁移水平与学生类型的交互作用不显著.这说明迁移水平的主效应在普通校的学生中不存在学生类型差异.这一结果与我们的设想基本一致.出现这一结果的原因可能是：普通校的大部分学生的知识结构不完善和认知水平相对较低，从而在样例学习的类比迁移中，解决认知负荷大的问题时，不能快速、准确地识别图式结构，进而提取解决问题的方法，大部分学生易受表面信息具体情节变化的影响，从而迁移不能顺利进行.

4.2 被试间因素效应分析与讨论

被试间因素效应检验的结果表明：学生类型对于普通校学生主效应十分显著.这说明普通学校中学生类型因素对迁移成绩影响十分显著.这一结果与我们的预期基本一致.结果说明，对于普通学校来说，问题解决的类比迁移成绩都存在学生类型上的差异.出现这种结果的原因可能是：不同类型的学生对解决过的问题的图式归纳方式不同，或者至少是侧重不同，学优生更善于或侧重于归纳出问题的结构特征，在解决新问题时能排除表面信息的干扰；而学中生和学差生往往不能很好的归纳出问题的结构特征而依赖问题的表面特征，最终保存在他们长时记忆中的更多的是关于问题的表面信息、不完整的结构信息，他们不能揭露表面特征的隐蔽条件，看到表面特征的隐蔽的相似性[12-13].

普通学校的学生类型与知识呈现方式两因素交互作用不显著.这一结果与我们预期的不完全一致.结果表明：普通学校的知识呈现方式不存在学生类型上的差异.出现这种结果的原因可能是：对于普通学校的学生，几乎都不能揭示隐蔽在表面特征下面的结构特征，储存在长时记忆中是表面的，非本质的特征，从而在解决新问题时易于受表面信息的干扰，使得迁移不能顺利进行.

5 结论

在研究中，迁移水平与学生类型因素对问题解决迁移影响显著，样例呈现方式与知识呈现方式的问题特征对解题方法的通达、提取和运用都没有影响.也就是说对于普通学校的学生来说，不管用哪种知识呈现方式，设计怎样的样例题，对余弦定理的解题迁移都没有明显影响.这一结果与示范学校的实验结果几乎一致.这为余弦定理教学设计提供了理论上的依据，不管是示范学校还是普通学校的学生，不同的样例呈现方式和知识呈现方式对余弦定理的迁移成绩没有明显的差异，设计不同水平的问题和学生类型是教学设计需要关注的变量.