圆锥曲线中相交圆的一个定点命题

李伟健

(安徽省滁州中学 239000)

近年，高考对“过圆锥曲线的焦点且互相垂直的两条弦”的性质进行了考察(2016年普通高等学校招生全国统一考试理科数学(乙)卷第20题).事实上，中学数学教师对过圆锥曲线的焦点且互相垂直的两条弦的性质早就给予了充分关注.林新建老师在文[1]指出以过圆锥曲线的焦点且互相垂直的两条弦为直径的圆的公共弦的中点轨迹是一个圆.叶良志、卢琼两位老师在文[2]进一步探索，得出如下命题：

命题1以过圆锥曲线的焦点且互相垂直的两条弦为直径的圆，公共弦所在直线经过定点.

尹惠民老师在文[3]中继续对这一结论进行了探索，发现将“过圆锥曲线的焦点”替换为“圆锥曲线内部的一个定点”，结论仍然成立.实际上，通过观察尹惠民老师的计算过程，可以发现，尹惠民老师在文[3]中实际上证明的是：

命题2以过平面内一定点的两条互相垂直的动直线与圆锥曲线的相交弦为直径的圆，公共弦所在直线经过定点.

本文对这一定点命题进行探究，发现文[3]中，两条弦所在直线垂直这一条件是多余的，即：

命题3以过平面内一定点的两条动直线与圆锥曲线的相交弦为直径的圆，公共弦所在直线经过定点.

下面分椭圆、双曲线和抛物线三种情形，对这一命题进行详细论证，并且在论证的过程中发现了两个有趣的推论，首先给出椭圆情形的证明.

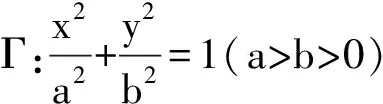
图1

证明设P(x0，y0)，A(x1，y1)，B(x2，y2)，当直线l，l′的斜率存在时，设直线l，l′的斜率分别为k，k′，那么直线l的方程为y=k(x-x0)+y0，l′的方程为y=k′(x-x0)+y0，

联立直线l和椭圆Γ的方程

消去y，得到

(b2+a2k2)x2+2a2(y0-kx0)kx+a2(y0-kx0)2-a2b2=0，

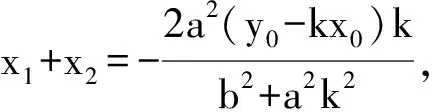
那么y1+y2=k(x1+x2-2x0)+2y0

y1y2=k2x1x2+k(y0-kx0)(x1+x2)+(y0-kx0)2

以AB为直径的圆的方程为

(x-x1)(x-x2)+(y-y1)(y-y2)=0，

整理可得

同理，以CD为直径的圆的方程为

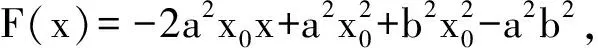
G(x，y)=a2y0x+b2x0y-a2x0y0-b2x0y0，

两个圆的方程相减，整理可得两圆公共弦所在直线m方程为：

(b2F(x)-a2H(y))(k+k′)+2G(x，y)(b2-a2kk′)=0，

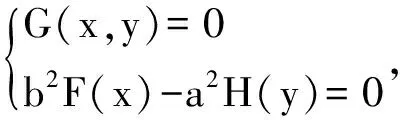
可以检验出方程有解，那么直线m经过以该方程的解为坐标的定点.

可以检验出当直线l或者直线l′的斜率不存在时，直线m仍然经过以方程

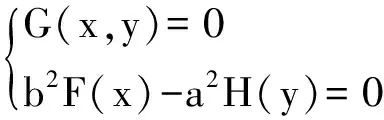
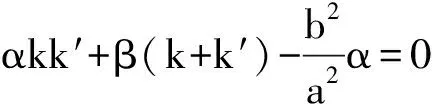
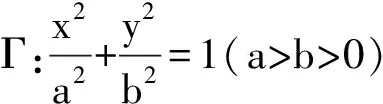
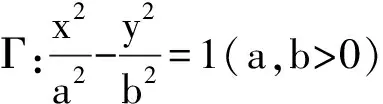
考虑到命题2和命题1证明相似，因此略去这一情形的论证.下面给出抛物线情形的证明.

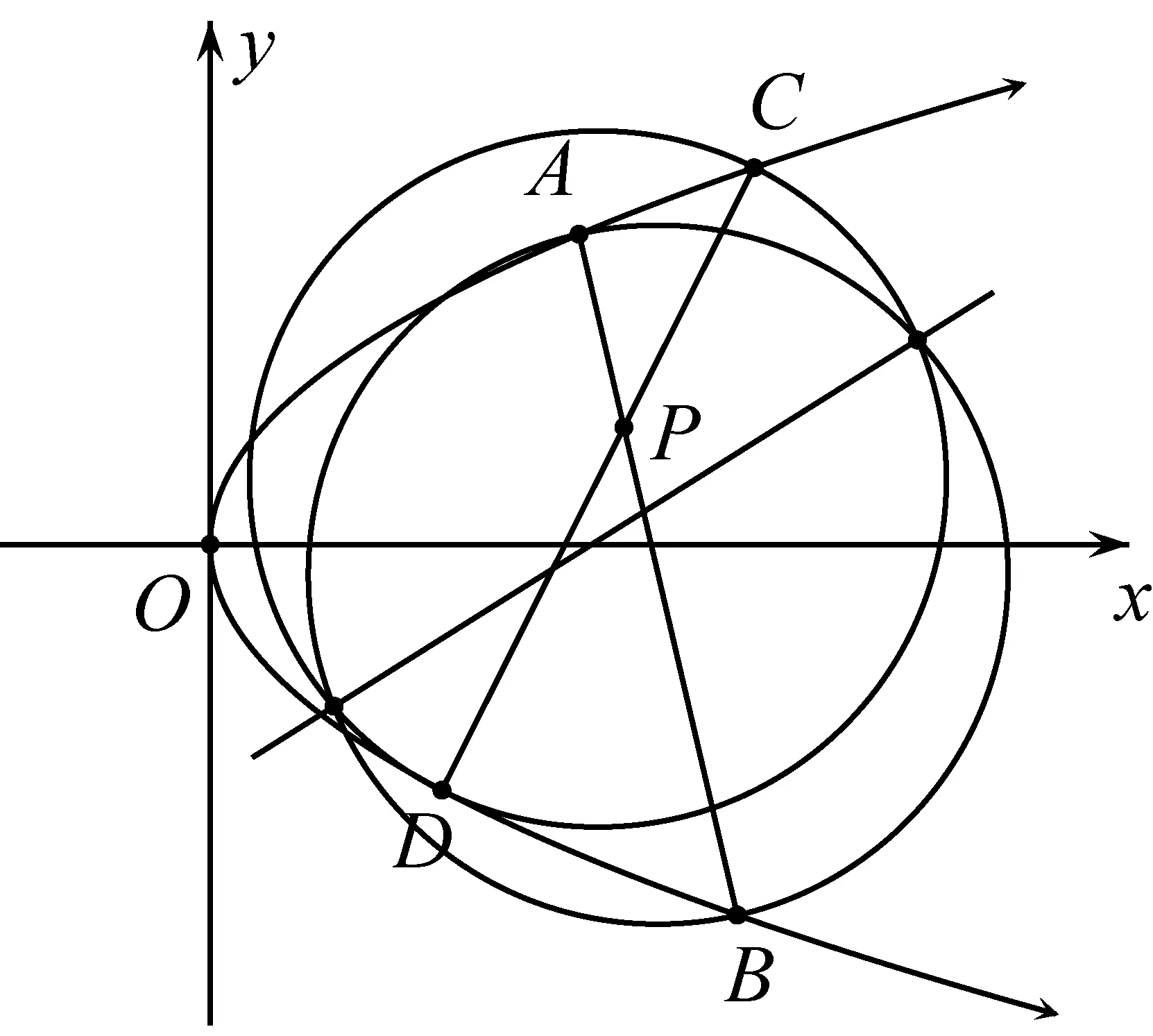
图2

命题3.3过点P作两条动直线l，l′分别交抛物线Γ：y2=2px(p>0)于点A、B，C、D.那么以AB为直径的圆和以CD为直径的圆公共弦所在直线m经过定点.

证明设P(x0，

y0)，A(x1，y1)，

B(x2，y2)，当直线l，l′的斜率存在时，设直线l，l′的斜率分别为k，k′，那么直线l的方程为y=k(x-x0)+y0，

l′的方程为y=k′(x-x0)+y0，

联立直线l和抛物线Γ的方程

消去y，得到

k2x2+2(ky0-k2x0-p)x+(y0-kx0)2=0，

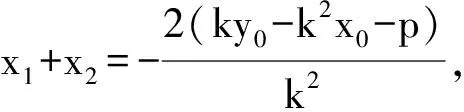
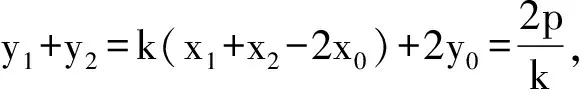
y1y2=k2x1x2+k(y0-kx0)(x1+x2)+(y0-kx0)2

以AB为直径的圆的方程为

(x-x1)(x-x2)+(y-y1)(y-y2)=0，

整理可得

同理，以CD为直径的圆的方程为

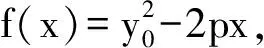
g(x，y)=xy0+py0-x0y0-py，

两个圆的方程相减，整理可得两圆公共弦所在直线方程为

f(x)(k+k′)+2g(x，y)kk′=0，

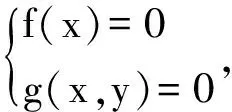
那么直线m经过以该方程的解为坐标的定点.

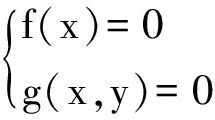
当直线l，l′的斜率k，k′满足αkk′+β(k+k′)=0(α，β是不全为零的常数)时，直线m的方程为αf(x)-2βg(x，y)=0.所以可得如下结论：

推论2过点P作两条直线l，l′分别交抛物线Γ：y2=2px(p>0)于点A、B，C、D，直线l，l′的斜率为k，k′且αkk′+β(k+k′)=0 (α，β是不全为零的常数).那么以AB为直径的圆和以CD为直径的圆公共弦所在直线m为一条定直线.

最后，需要指出的是，如果两圆的公共弦不存在时，那么本文提出的命题3反映的则是两圆的根轴的性质.