“加权”思想在数据分析中的应用探究

郝进宏

(北京市第一五六中学 100034)

当前我国的数学教学改革正在向纵深发展，新的课程标准强调对学生数学核心素养的培养.孔凡哲、史宁中[1]指出：数学核心素养的本质在于用数学的眼光观察现实世界、用数学的思维思考现实世界、用数学的语言表达现实世界的综合素养，数学核心素养包含三种成分：一是学生经历数学化活动而习得的数学思维方式，二是学生数学发展所必需的关键能力，三是学生经历数学化活动而习得的数学品格及健全人格的养成. 其中关键能力包括数学抽象能力、数学推理能力、数学建模能力、直观想象能力、运算能力和数据分析观念.

下面笔者以2016年北京高考理科第16题为例，来总结提炼“加权”思想在求解期望问题中的应用，并用提炼的思想方法解决2018年北京西城一模理科16题和2018年北京高考理科第17题，希望以此进一步深入体会数据分析在提高学生数学能力素养方面的作用，请同行不吝赐教.

1 问题的提出、分析及总结

1.1 问题的呈现

近几年来，北京高考中概率统计最后一问，题目要求往往是“结论不要求证明”，也就是重直观轻计算，如果按部就班地计算，过大的计算量和学生较低的运算能力会大大降低做题的效率，进而影响考试的节奏和成绩. 如果学生对相应问题理解得比较透彻，选用的方法恰当，那么往往会高效解决这类问题.

例1(2016年北京高考理科第16题)A,B,C三个班共有100名学生，为调查他们的体育锻炼情况，通过分层抽样获得了部分学生一周的锻炼时间，数据如下表(单位：小时)：

表1.1

(Ⅰ)略；(Ⅱ)略；

(Ⅲ)再从A,B,C三个班中各随机抽取一名学生，他们该周的锻炼时间分别是7,9,8.25(单位：小时)．这3个新数据与表格中的数据构成的新样本的平均数记为μ1，表格中数据的平均数记为μ0，试判断μ0和μ1的大小．(结论不要求证明)

1.2 问题的分析

若从A，B，C三个班中各随机抽取一名学生，他们该周的锻炼时间分别是7，9，8.25，数据变成如下表1.2所示，要比较两组数据的均值大小，最基本的方法就是算出两组数据的平均值，即

由上式看出这种方法计算量很大，在高考的有限时间内如果用很长时间去获取这三分有所不值，而且对于计算能力不足的学生可能既花费了时间但最终又没能得出正确结论，因此这种方法解题效率非常低.

表1.2

观察新增的7，9，8.25这三个数，它们和A，B，C三组数据有何关系？我们发现7，9，8.25这三个数分别是增加数据前A，B，C三组数据的平均值，换句话说新增的三个数没有改变三组数据的平均值. 因此上面的计算可以简化如下：

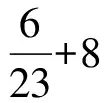
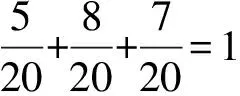
按照这一思想，我们比较μ0和μ1中7， 8.25，9的权重大小，9的权重之差为

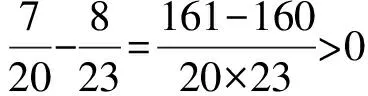
8.25的权重之差为

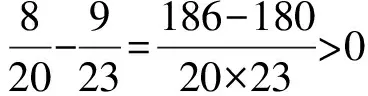
即在μ0中较大的两个数9和8.25的权重都比μ1中对应数值的权重大，因此μ0>μ1.

从分析过程我们可以感知到：从“加权”角度来思考这个问题，解题效率大大提高，而且这一思想方法为我们提供了研究数据的一个新的角度，下面我们通过反思来探讨一下这些计算平均值的方法之间的联系.

1.3 问题的反思

该题的解决思路实际上来源于平均值的两种定义.下面我们给出这两种定义方法，并由此提炼出第三种定义，通过比较分析它们之间的关系以便进一步深刻理解均值的涵义.

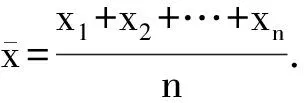
该定义是我们中学对于平均值的定义，其直观性比较强，学生记忆深刻，是学生求均值最常用的方法，如果x1,x2,…,xn中有相同数据，那么我们还可以将定义1简化为如下定义2.

定义2[2]如果这n个数中有相同的，不妨设其中有ni个取值为xi，i=1,2,…,k，则其均值为：

那么有一个问题，如果数据x1,x2,…,xn没有相同的，加权平均的想法还适用吗？

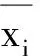
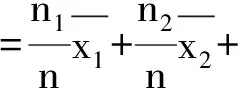
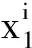
实际上2016年北京高考理科卷第16题就是利用定义3的思想方法求解的. 利用定义3，我们得到μ0和μ1是7， 8.25，9的加权平均值，所以只要比较这三个数的权重大小立刻就能比较出μ0和μ1的大小. 加权思想实际上是对数据处理后的一种简化的计算方法，其本质有助于理解概率论中随机变量期望的定义.

2 方法的应用

下面我们利用加权思想来解决2018年北京西城一模理科第16题和2018年北京高考理科第17题.

2.1 问题一的呈现与分析

例2(2018年北京市西城区一模理科16题)某企业2017年招聘员工，其中A、B、C、D、E五种岗位的应聘人数、录用人数和录用比例(精确到1%)如下：

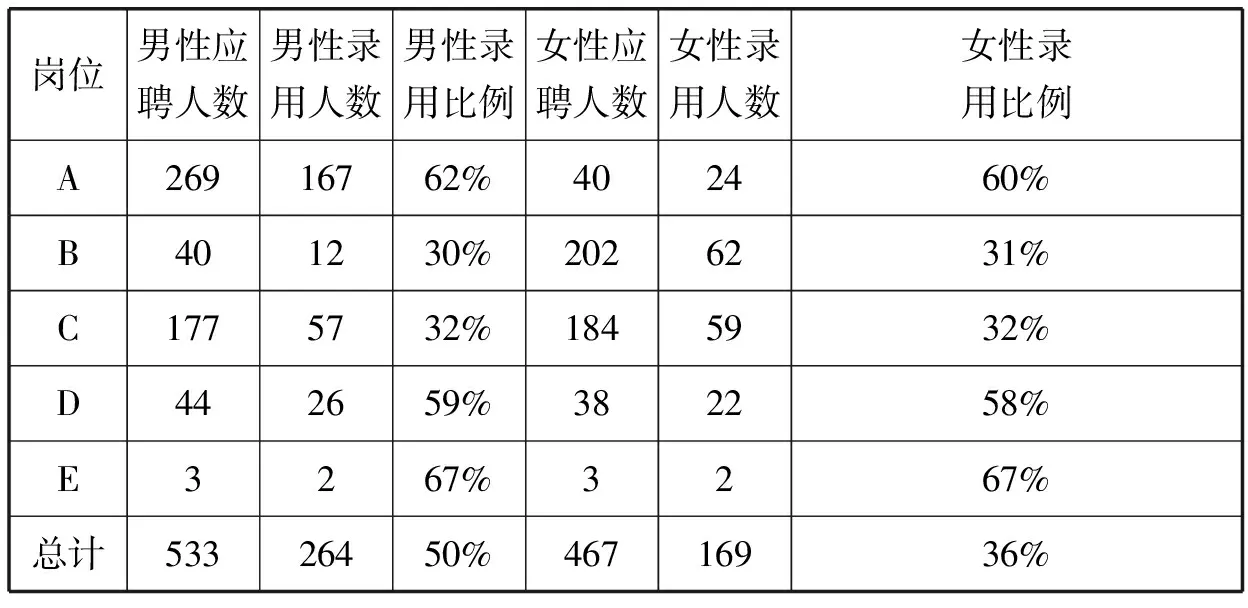
岗位男性应聘人数男性录用人数男性录用比例女性应聘人数女性录用人数女性录用比例A26916762%402460%B401230%2026231%C1775732%1845932%D442659%382258%E3267%3267%总计53326450%46716936%

(Ⅰ)略；(Ⅱ)略；

(Ⅲ)表中A、B、C、D、E各岗位的男性、女性录用比例都接近(二者之差的绝对值不大于5%)，但男性的总录用比例却明显高于女性的总录用比例．研究发现，若只考虑其中某四种岗位，则男性、女性的总录用比例也接近，请写出这四种岗位．(只需写出结论)

通过观察发现C、D、E三组男女应聘人数、录用人数和录用比例相当，而A、B两组尽管男女录用比例相当，但是两组的男女应聘人数以及录用人数差距非常大，所以直观上，男女总的录用比例的差距应该主要是由A、B两组数据的差异引起的，那么到底是A还是B，学生就犯难了.

接下来我们利用加权思想来解决该问题.

设男女生的总的录用比例分别为k1和k2，其表达式如下：

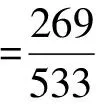
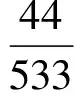
因此要想保留男性、女性的总录用比例也接近，需要剔除A组数据.

2.2 问题二的呈现与分析

例3(2018年北京高考理科第17题)电影公司随机搜集了电影的有关数据，经分析整理得到下表：

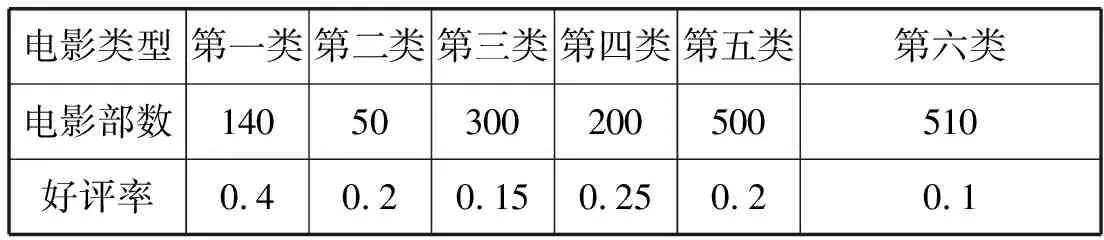
电影类型第一类第二类第三类第四类第五类第六类电影部数14050300200500510好评率0.40.20.150.250.20.1

好评率是指：一类电影中获得好评的部数与该类电影的部数的比值.

假设所有电影是否获得好评相互独立.

(Ⅰ)略；(Ⅱ)略；

(Ⅲ)假设每类电影得到人们喜欢的概率与表中该类电影的好评率相等，用“ξk=1”表示第k类电影得到人们喜欢，“ξk=0”表示第k类电影没有得到人们喜欢(k=1,2,3,4,5,6).写出方差Dξ1,Dξ2,Dξ3,Dξ4,Dξ5,Dξ6的大小关系.

这道高考题的第三问，学生普遍反映比较难无从下手. 我们用两种方法来解决.

方法一以第一类电影为例，电影部数是140，好评率为0.4，则共有140×0.4=56部电影获得好评，并且其得分为1，未获得好评的电影有94部，得分为0，140部电影得分均值为0.4，所以方差

=(1-0.4)2×0.4+(0-0.4)2×0.6

=0.4×0.6，

由此我们发现其对应方差为p(1-p)，同理，

Dξ2=0.2×0.8，Dξ3=0.15×0.85，

Dξ4=0.25×0.75，Dξ5=0.2×0.8，

Dξ6=0.1×0.9，

因此方差大小关系为

Dξ1>Dξ4>Dξ2=Dξ5>Dξ3>Dξ6.

由分析过程我们发现，本质上，方差也是一种加权平均值，从加权平均值角度去计算和比较方差可以更透彻地理解方差的意义.

反思

实际上，第三问的假设“每类电影得到人们喜欢的概率与表中该类电影的好评率相等”提示我们可以将每部电影的得分看成一个随机变量，如果找出该随机变量的分布很快就能求出随机变量的方差，最终求得结果.

由于每部电影的得分实际上服从n=1的二项分布，即两点分布，设得分为ξ，P(ξ=1)=p，P(ξ=0)=1-p，我们知道两点分布的方差为Dξ=p(1-p)，与我们的计算结果一致.

尽管与反思的方法比，方法一和方法二有些繁琐，但是对于中学生来讲，这个过程具有深远的意义，同学们可以通过亲手计算去探索发现数学问题背后的数学原理，进而进行提炼和总结，最终提升学生的综合素养.

3 结语

数据分析已经变成我们日常生活中的必要组成部分，在日常的教学中，我们不仅要重视教授学生搜集、整理数据的方法，而且还要引导学生如何分析得到的数据并根据所得结论作出合理的判断和决策. 因此，如果我们重视应用“加权”的思想处理、分析数据平均值的基本方法，那么既能提高解题效率，又能增强对数据整体特征的把握，从而从整体上提升学生的数学素养.