例谈数学教学的“追问”策略
马 驰
(江苏省昆山中学 215300)
1 问题的提出
追问是课堂教学中提问的“后续动作”,是教师在学生回答问题的过程中或者问题回答结束后的“下一个”教学步骤和教学策略.追问集中体现了教师的教学素养、教学机智、教学水平和能力;更重要的是,追问是学生在教师引导下的一个“再创造”的过程,可以及时地启发和激发学生的思维,拓宽思维的广度,增进思维的深度,锻造思维的强度.
追问是一种机智,追问更是一门艺术.所以,追问不等于滥问、乱问,除了要与前一问形成一定的关系之外,还需要讲求追问的时机和方式.那么,怎样才能在课堂上做到“追”有收获、“问”有共鸣呢?数学教学的“追问”是要有策略的,以下是笔者自己的一些浅薄见解,以求各位读者的批评指正.
2 追问要关联“原点”
追问,是针对某一内容或某一问题,为了使学生弄懂弄通,在一问之后的再次提问,穷追不舍,直到学生能正确理解.但是,现在的数学课堂上的“问”和“追问”几乎可以用“狂轰滥炸”、“杂乱无章”来形容,“无绪”反倒成了其最主要的特征.因此,追问一定要与前一个问题有某种内在关联,即追问要关联原问题的出发点.下面以苏教版必修二“平面与平面的位置关系的判定(1)”教学中的几个片段为例说明.
2.1 可以是类比关联
当人们面临一个比较生疏的问题时,往往可以联想一个比较熟悉的问题作为类比对象,熟悉问题的解决途径和方法可以启发我们得到生疏问题的解决途径和方法.例如,在开展新课的引入部分时,可以不妨先提一问:“前面我们研究的空间中两直线的位置关系是什么?按公共点个数如何划分?”明确“位置关系”很容易,但不能到此为止,于是追加一问“空间中的直线与平面的位置关系又有哪些?按公共点个数如何划分?”提升维度,强调以“公共点个数划分”为方向,再次追加一问“点、线、面作为空间几何中的三个基本元素,你认为接下来的空间中的面面可能有哪些位置关系呢?”,引出本节课内容.
2.2 可以是递进关联
沿一条直线向前推进,步步深入,将问题引向纵深,而不是“原地转圈”,后一问的思维深度要大于前一问,直到弄清问题的实质为止.例如,当学生可以根据“公共点个数划分”来区分空间中平面与平面的位置关系时,可以提问“请同学们填写下面的表格:”(如下表1)
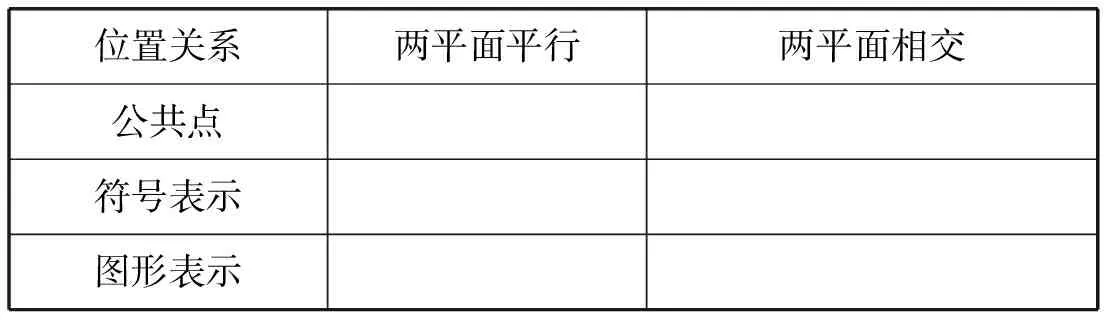
表1
用符号表示给学生数学抽象,以图形表示让学生直观想象.此时的学生头脑中对“面面位置关系”与“公共点个数”建立起了对应,这时追加一问“两个平面没有公共点,那么就说这两个平面互相平行.然而,平面是无限延展的,如何确定它们是否一定没有公共点呢?”有限到无限,将问题引向了纵深,将问题引出了冲突,引出了学生的思考.
2.3 可以是补充关联
维果斯基的“最近发展区理论”认为,学生的发展有两种水平:一种是学生的现有水平,另一种是学生可能的发展水平.两者之间的差距就是最近发展区.当学生得到了空间中面面可能有的位置关系后,教师应该给出本节课要研究的位置关系——面面平行,并且可以通过实例让学生观察感受,此时抛出一问“平面与平面平行该如何判定呢?”学生要从感性的认识变成理性的判定,这是有难度的(除了已预习的学生能回答).基于“最近发展区理论”,不妨设置一问“线面平行的判定定理是什么?线面垂直的判定定理是什么?”以此问让学生自我回顾最近学习的内容,但不能到此为止,追加一问“体现了怎样的转化?”明确“线线关系”推导“线面关系”,让学生体会“降低维度”考虑问题,得到“线面关系”推导“面面关系”,揭示问题的本质.
2.4 可以是拓展关联
由此及彼,以点带面,将问题适当向外延伸开去,拓宽问题的面,拓展学生的思维,从而将学生的思维引向比前一问更高更远的地方.例如,笔者对于定理的给出,设计了实验操作(将学生分成若干小组)“请同学们将桌上的三角板和一个平行四边形的纸板分别在手中摆放成与桌面平行的状态,组内先讨论为什么要这样摆?”实验的目的是引导学生通过动手操作,从直观上感知平面与平面平行,最终进行抽象概括,给出定理的猜想.而猜想的结论是否可以作为“定理”?当中的关键词是否已经弄清楚?这些可以通过追问进行拓展延伸,“只满足一条直线与平面平行能否判定面面平行?你在探究过程中能找到反例吗?”,“为什么要求‘两条相交直线’,不相交的两条直线能否可以判定面面平行?你在探究过程中能找到反例吗?”.通过已操作的实验,进行合理的判断,教师给出判断方向,学生得到正确的认识,对猜想的结论进行完善, “追问”在其中起到了“一石激起千层浪”的效果.
追问不是乱问,更不等于滥问,一定要把握好与前一问之间的关联之处,无论是要理解的内容还是要激发的思维,两者间都要有某种内在的、必然的联系.笔者以为,前一问的具体内容和思维角度应该是追问的“原点”.
3 追问要彰显“智慧”
追问难预设.所以,从实质上来说,追问其实就是所谓的“急中生智”,这也充分说明为什么追问会是教师教学机智的直观表现.追问能“显智”,这“智”主要体现于教师应该在什么情况下需要或值得再去“追一问”.下面以苏教版必修三“几何概型(1)”教学中的几个片段为例说明.
3.1 要善于对症出击
一个教学环节的成功,很重要的一点就是得益于教师能及时地抓住师生间对话时出现的问题,对症出击,且紧扣不放,穷追到底.因为正是这样的追问,才能充分调动起学生的思维,使学生始终处于一种紧张和深度开发的状态.这就要求教师要始终全神贯注于学生的言说,敏锐地捕捉学生思维中出现的问题和不足,或做提醒,或做补充.
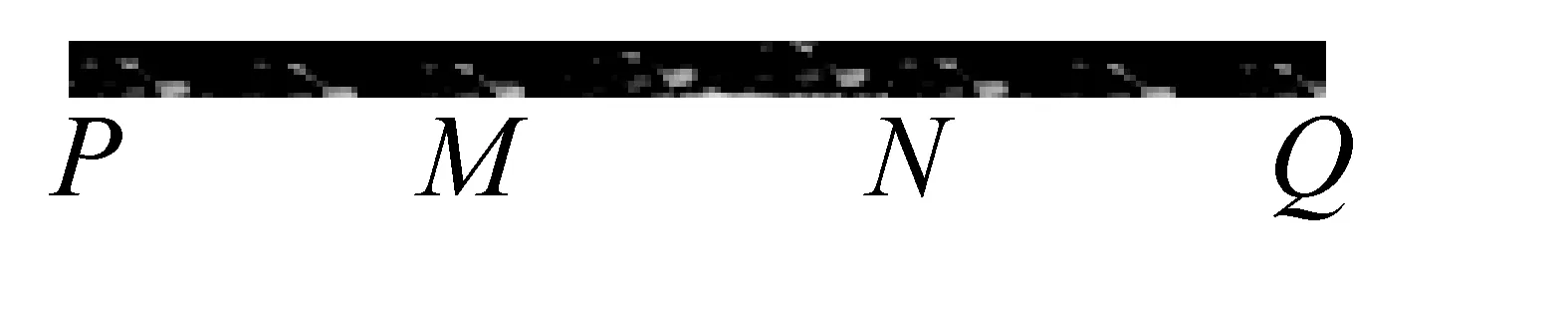
图1
例如,笔者在引入部分针对给出的引例“取一根长度为3 m的绳子(如图1),如果拉直后在任意位置剪断,那么剪得两段的长都不小于1 m的概率有多大?”
设置了如下的一些问题:
问题:试验中的基本事件是什么?
追问1:每个基本事件的发生是等可能的吗?
追问2:符合古典概型的特点吗?
追问3:这个问题的概率是多少呢?
通过提问并追问,引导学生回顾古典概型的特点:有限性和等可能性.发现这个问题虽然貌似古典概型,但是由于这个问题中的基本事件应该是“在绳子的每一处将绳子剪断”,所以有无限多种情况,不满足有限性这个特点,因此不是古典概型.也就是说,我们不能用古典概型的概率公式去解决这个问题.通过追问,让学生产生对概型认识的困惑;通过追问,让学生产生对新的问题解决的饥渴;通过追问,让学生产生对预授知识的向往.
3.2 要适时雪中送炭
在教学追问的环节中,首先强调的是预设,要求的就是教师自身对问题的理解和把握要深刻全面,因为只有“手中有粮”,心中才能不慌;其次还要求教师在学生的思维受阻之时能够及时“出手相救”,给学生雪中送炭,充分发挥教师的引领和点拨作用,而不能置身事外、“冷眼旁观”,否则,极有可能会让学生的思维“雪上加霜”.这同样要求教师课堂上要集中注意力,全神贯注地参与对话的整个过程.
教师引导:将基本事件视为一个点,在绳子PQ上每剪一次的“位置”即对应着线段PQ上一“点”.
问题:在绳子MN上每剪一次的“位置”对应着什么呢?
追问1:无数次地随机剪绳子PQ的“位置” 对应着什么呢?
追问2:无数次地随机剪绳子PQ的“位置”的总和可视为什么呢?
追问3:根据上述分析,你能否完成下表2?
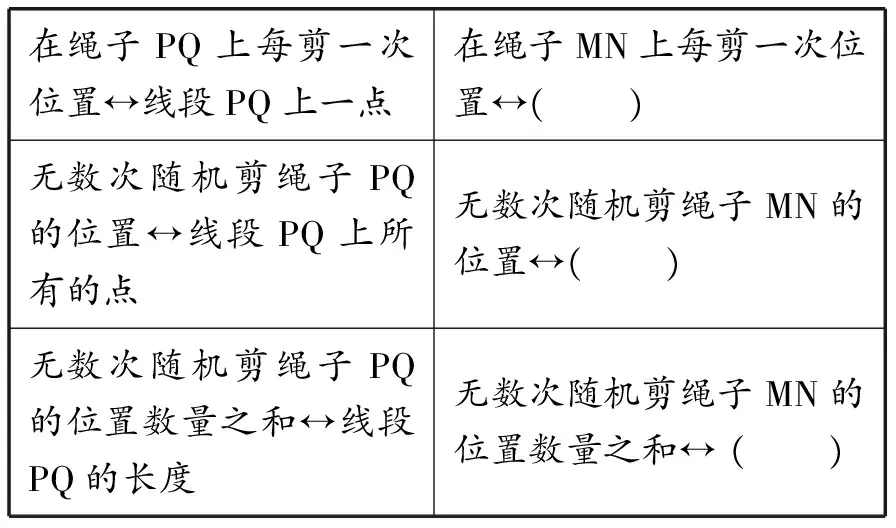
表2
最终,从“数(剪的次数)↔形(点)↔数(线段的长度)”,解决“无数比无数”的情况.
通过上面的分析,引导学生发现:几何概型与古典概型的区别在于它的试验结果不是有限个,但是它的试验结果在一个区域内均匀地分布,因此它的基本事件满足无限性和等可能性,将基本事件视为一个点,点均匀的铺满整个区域,且这个区域可度量.追问不是“逼问”,而是引导,发起者是教师,受益者是学生,给其线索,探得“宝藏”.
3.3 要顺势趁热打铁
机智的教师常常会“顺势一击”,抓住一点,轻巧地将学生的思维引向辽远.因为有的时候从表象上看,教师所提的问题似乎已经得到了较为圆满的解决,但是学生的思维还有可拓展或开掘的可能和空间,那么,我们就不能让学生的思维仅止于此,不妨乘势而上、趁热打铁,再追一问,从而拓宽思维的广度、增进思维的深度.
例如,在概念运用环节教材上一例题如下:
在1 L高产小麦种子中混入了一粒带麦锈病的种子,从中随机取出10 mL,含有麦锈病种子的概率是多少?
学生运用几何概型的概率求解公式顺利地得到解答:
解:取出10 mL麦种其中“含有病种子”这一事件记为A,则
此时,笔者追一问:“请问这道题中的基本事件是什么?”学生的回答五花八门,而无一是处,究其原因,那就是“轻概念理解,重公式运用”而造成.所以,此处的追问是“及时雨”,不仅拓展了学生的思维,更是加深了问题的理解———“这粒带麦锈病的种子可能出现的位置”是基本事件.
无论是对症出击、雪中送炭还是趁热打铁,追问都要讲求适时、相机而问,这也许就是所谓的“智慧”.追问能“显智”,强调的是追问的方式.只有追的“及时”,问的“恰当”,这样的追问才有力度,学生的思维才有广度与深度,课堂才有厚度.
4 追问要讲究“良机”
追问的策略,是对学生思维行为作“即时”的点拨和有效的控制,让追问真正成为师生互动的平台,更好地促进学生的思维发展,提高课堂教学的有效性,而这“即时”就是我们所要把握的时机、要掌握的“火候”.下面以苏教版选修2—1中“双曲线的标准方程(1)”教学中的几个片段为例说明.
4.1 追问于混沌状态
不确定性和无序性,是思维混沌状态的重要特点,所谓“山重水复疑无路”,说的也许正是这种现象.而学生的思维一旦出现了混沌状态,其实也就出现了一个值得我们去把握的“良机”,一个需要教师适时追问、点拨的时机.这个时候教师不能“袖手旁观”,恰当的追问,或许就会收到“柳暗花明又一村”的效果.
例如,本节课的引入以“拉拉链”的实验给出,让学生观察“点M”的轨迹,让学生说出“点M”应满足的条件,即|MF1|-|MF2|为定值,此时给出问题:
“你能否类比椭圆定义,给出该曲线的定义?”
学生甲给出自己的定义“平面内到两定点F1,F2的距离之差为一常数的点M的轨迹”,但其他学生中的议论更是激烈,这正是“追问”的好时机:
追问1:当常数等于|F1F2|时,轨迹是什么?
追问2:当常数大于|F1F2|时,轨迹是什么?
追问3:当常数等于0时,轨迹是什么?
此处的“追问三连击”让学生注意到了学生甲给出的定义中漏掉了常数应为“小于|F1F2|的正数”这个条件,让他们对该曲线的定义进行了“修正”.“ 追问”让他们走出了混沌状态,进而引出双曲线的定义来.
4.2 追问于临界状态
追问追求的是一种“激活效应”,孔子早就说过要“不愤不启,不悱不发”,而这“愤”这“悱”,就是追问的前提和时机.所以,只有当学生的思维处于由活跃到受阻时、似懂非懂时实施追问,才能使学生的思维在临界点上产生顿悟、发生质的飞跃;如果学生的思维尚未进入临界状态就去“追”,就不能体现出点拨的作用,追问也就不能收到我们预期的、比较明显的效果.
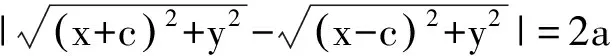
“这个等式如何化简呢?”
学生乙说:两边平方.学生丙说:不行,次数太高!两个根式相乘运算又复杂,故去掉绝对值移项后再平方.于是,笔者请学生丙上黑板给出了板演过程,学生鼓掌称赞.课前,笔者做了预设,此处化简正是可以作为提升学生核心素养“数学运算”的好素材,此时的学生思维已激活,追问可助其“开窍”,所以笔者又问学生乙“你两边平方后是怎样的形式?”学生乙给出如下式子:
(x+c)2+y2+(x-c)2+y2-
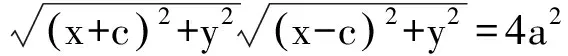
追问1:如果再平方,次数太高,能否降次呢?
追问2:能否进行换元,令t=x2+y2+c2呢?
学生乙心领神会,顺利的给出了化简过程,如下:

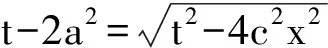
⟹a2t-c2x2=a4
⟹a2(x2+y2+c2)-c2x2=a4
⟹(c2-a2)x2-a2y2=a2(c2-a2).
“追问”的作用在于启发,让学生的思维得到质的飞跃.
4.3 追问于僵持状态
追问的目的是为了帮助学生突破思维的“瓶颈”,因为在课堂教学过程中,学生的思维一般情况下不太可能是一帆风顺、畅通无阻的,总会有暂时停滞、相持不下的时候,特别是教师提出的问题带有一定的思维难度时,如果教师能够抓住这个时机追上一问,或许就能突破“僵持”的“瓶颈”.
例如,在本节课的课堂小结时,笔者问“通过这节课的学习,你有何收获?”学生的回答在意料之中——“认识了双曲线,理解了双曲线的定义和标准方程,并会写出焦点坐标等”.此时的学生,通过对双曲线的标准方程的认识做了一两道例题,思维停留在双曲线的标准方程上,无法抓住本节课探究的价值和意义,所以,在此追问,可以让学生突破“僵持状态”,让认识和理解得到很好地提升:
追问1:本节课我们以椭圆类比双曲线得到了定义、标准方程等内容,请同学们想想除了动点到两定点的距离和、距离差,还可以类比成什么呢?
追问2:距离的商呢?
类比无限,想象无穷!追问就应给学生打开想象的大门.
总之,只有学生在进行了充分的思考之后,思维处于一种由“起点”迈向“终点”但尚未达到“终点”的中间靠后状态时,追问才是最有效的.
5 结语
追问是教师教学智慧的展示,追问是锻造学生思维的手段,追问更是课堂教学的艺术.陶行知说过:“行是知之路,学非问不明.”适时地、有创意的追问是课堂机智的充分表现.“关联原点”、“彰显智慧”和“讲究良机”是数学教学中追问组成的三个关键要素,构成了追问的整体策略.

