导数综合题之谋略
■河南省平顶山市第一高级中学 刘海洋
■河南省平顶山市第一中学 张玲敏
众所周知,导数的综合应用题具有较高的难度,同学们“征服”它不仅要有勇气,而且要有智慧。那么解答这类问题需要哪些谋略呢?下面举例说明,供同学们参考。
一、利用分类讨论思想探究函数性质问题
例1函数f(x)=x3+|x-a|(x∈R,a∈R)。
(1)若函数f(x)在R上为增函数,求a的取值范围;
(2)若函数f(x)在R上不单调时,记f(x)在[-1,1]上的最大值、最小值分别为M(a)、m(a),求M(a)-m(a)。
解析:由已知可得:

令h'(x)=0,得x=±1,所以h(x)在(-∞,-1)和(1,+∞)上是增函数,在(-1,1)上为减函数。
(1)分析可知,若要满足f(x)在R上是增函数,则需要a≤-1。
故a的取值范围为(-∞,-1]。
(2)因为函数f(x)在R上不单调,所以a>-1。
当-1<a<1时,f(x)在(-∞,-1)上是增函数,在(-1,a)上是减函数,在[a,+∞)上是增函数。
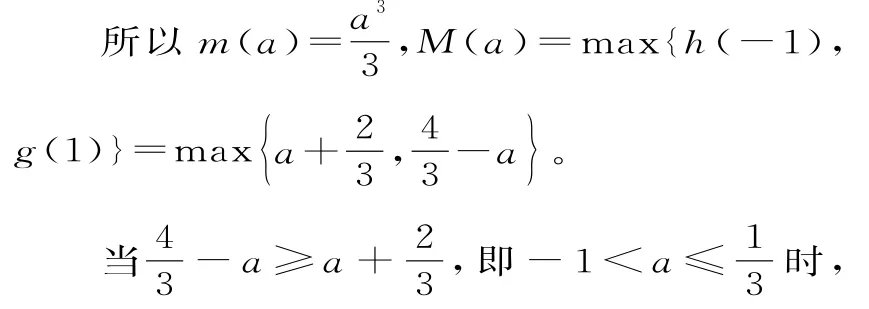

【方法感悟】
1.解答这类题的模板:

2.解答这类题的难点:
(1)何时讨论参数?由于题目条件的不同,有的在求零点时讨论,有的在列表时讨论。
(2)如何讨论参数?需要根据题目的条件而定,有时还需参考自变量的取值范围,讨论的关键是做到不重不漏。
二、利用数形结合思想探究函数的零点问题
例2设函数f(x)=lnx+,m∈R。
(1)当m=e(e为自然对数的底数)时,求f(x)的极小值;
解析:(1)由题设知,当m=e时,f(x)=
当x∈(0,e)时,f'(x)<0,f(x)在(0,e)上单调递减。
当x∈(e,+∞)时,f'(x)>0,f(x)在(e,+∞)上单调递增。
因此,f(x)的极小值为2。
则φ'(x)=-x2+1=-(x-1)(x+1)。
当x∈(0,1)时,φ'(x)>0,φ(x)在(0,1)上单调递增;
当x∈(1,+∞)时,φ'(x)<0,φ(x)在(1,+∞)上单调递减。
故x=1是φ(x)的唯一极值点,且是极大值点。
又φ(0)=0,结合y=φ(x)的图像(如图1),可知:
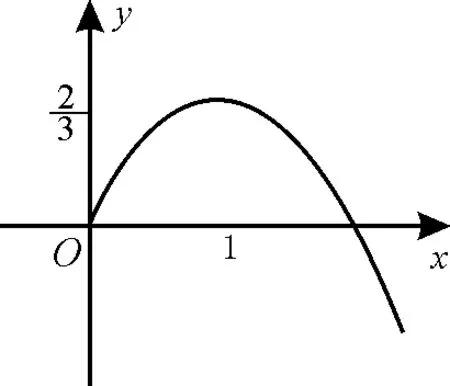
图1
④当m≤0时,函数g(x)有且只有一个零点。
【方法感悟】
利用导数探究函数零点的一般思路:
(1)转化为可用导数研究其函数的图像与x轴(或直线y=k)在该区间上的交点问题;
(2)利用导数研究该函数在该区间上的单调性、极值(最值)、端点值等性质,进而画出其图像;
(3)结合图像求解。
三、利用函数思想探究证明不等式问题
例3已知函数f(x)=ex+m-x3,g(x)=ln(x+1)+2。(1)若曲线y=f(x)在点(0,f(0))处的切线斜率为1,求实数m的值;
(2)当m≥1时,证明:f(x)>g(x)-x3。
解析:(1)因为f(x)=ex+m-x3,所以f'(x)=ex+m-3x2。
因为曲线y=f(x)在点(0,f(0))处的切线斜率为1,所以f'(0)=em=1。
解得m=0。
(2)因为f(x)=ex+m-x3,g(x)=ln(x+1)+2,所以f(x)>g(x)-x3等价于ex+m-ln
(x+1)-2>0。
当m≥1时,ex+m-ln(x+1)-2≥ex+1-ln
(x+1)-2。
因此,要证ex+m-ln(x+1)-2>0,只需证明ex+1-ln(x+1)-2>0。
设h(x)=ex+1-ln(x+1)-2,则
设p(x)=ex+1-(x> -1),则
所以函数p(x)=h'(x)=ex+1-(-1,+∞)上单调递增。
因为h'(x0)=0,所以ex0+1=ln (x0+1)=-(x0+1)。
当x∈(-1,x0)时,h'(x)<0;当x∈(x0,+∞)时,h'(x)>0。
所以当x=x0时,h(x)取得最小值h(x0)。
因此,h(x)≥h(x0)=ex0+1-ln(x0+1)
综上可知,当m≥1时,f(x)>g(x)-x3。
【方法感悟】
1.利用导数证明不等式的基本步骤:(1)作差或变形;(2)构造新的函数h(x);(3)利用导数研究h(x)的单调性及最值;(4)根据单调性及最值,得到所证不等式。
2.构造辅助函数的四种方法
(1)移项法:证明不等式f(x)>g(x)(f(x)<g(x))的问题转化为证明f(x)-g(x)>0(f(x)-g(x)<0),进而构造辅助函数h(x)=f(x)-g(x)。
(2)构造“形似”函数:对原不等式同解变形,如移项、通分、取对数;把不等式转化为左右两边是相同结构的式子的结构,根据“相同结构”构造辅助函数。
(3)主元法:对于(或可化为)f(x1,x2)≥A的不等式,可选x1(或x2)为主元,构造函数f(x,x2)(或f(x,x1))。
(4)放缩法:若所构造函数最值不易求解,可将所证明不等式进行放缩,再重新构造函数。
四、利用转化与化归思想探究不等式恒成立问题
例4已知函数f(x)=lnx。
(1)求函数g(x)=f(x+1)-x的最大值;
(2)若对任意x>0,不等式f(x)≤ax≤x2+1恒成立,求实数a的取值范围。
解析:(1)因为f(x)=lnx,所以g(x)=f(x+1)-x=ln(x+1)-x(x>-1)。

当x∈(-1,0)时,g'(x)>0,g(x)在(-1,0)上单调递增;
当x∈(0,+∞)时,g'(x)<0,g(x)在(0,+∞)上单调递减。
故g(x)在x=0处取得最大值g(0)=0。
(2)因为对任意x>0,不等式f(x)≤ax≤x2+1恒成立,所以:在x>0上恒成立,进一步转
当x∈(1,e)时,h'(x)>0;当x∈(e,+∞)时,h'(x)<0。
【方法感悟】
利用转化与化归思想解决不等式恒成立问题的“两种”常用方法:
(1)分离参数法:

(2)函数思想法:


