兰新高速铁路高寒地段路基温度场数值模拟分析

戚志刚,杨增丽,沈 鑫,杨有海

(1.中国铁路兰州局集团有限公司工务处,兰州 730000； 2.兰州交通大学土木工程学院,兰州 730070)

引言

兰州至乌鲁木齐高速铁路(以下简称“兰新高速铁路”)浩门至大梁区间所处地区海拔高，气温低，冻结期长，属于深季节性冻土区。由于其高寒阴湿的环境，在低温作用下路基会产生不同程度的冻胀变形[1]。虽然高速铁路路基基床底层采取冻胀不敏感的防冻胀填料，但在冻结深度较大的条件下路基仍会产生较大的冻胀量，造成轨面不平顺，将影响线路安全、列车正常运营。因此掌握季节性冻土区路基冻结深度，对路基冻害的防治尤为重要。

目前，通过实测和数值模拟的方法对冻土区的路基温度场已经有了一定的研究。牛富俊等[2]对兰新高速铁路浩门至大梁区间运营期间路基断面不同深度的温度进行监测，分析在冻结期路基不同深度下的温度场季节变化规律。张玉芝等[3]、韩春鹏等[4]、司剑锋[5]等通过实测的方法对不同地区位于季节性冻土区/多年冻土区的铁路/公路的路基温度场进行分析，并总结出不同地区路基温度场的变化规律及变化特征。朱林楠[6]为方便确定热量的上边界条件，提出了气温与下垫面附面层底面温度直接相关的方程。白青波等[7]在路基温度场模拟中的上部热边界条件研究中，给出了附面层厚度的确定方法。在给定附面层厚度条件下，通过数值模拟分析，得到了附面层底部温度增量的计算公式和设计图表。王铁行等[8]通过综合考虑路基走向、风速、辐射、蒸发等多种因素，提出了在一、二、三类边界条件下考虑诸多因素的有限元计算方法，给出了相应计算公式。易鑫等[9]在附面层原理的基础上，考虑采用带有相变的控制方程和数值方法，选取不同的年平均气温为影响因素，对青藏工程走廊公路路基的人为冻土上限和年平均地温进行了研究。李彬嘉等[10]采用显热容法，针对冰-水相变对隧道温度场的影响进行研究，对比分析了考虑相变与否两种情况下的动态温度场差异。韩铠屹等[11]、马勤国等[12]、毛雪松等[13]、董连成等[14]、梁波等[15]依托不同背景下的路基，利用不同的计算方法对路基温度场进行数值模拟，得出在不同因素影响下的路基温度场变化规律，为研究冻土路基温度场的变化规律提供了可靠依据。吕菲[16]通过室内模型试验表明，XPS保温板具有良好的保温隔热作用，并且保温措施有效控制了哈齐客专路基A、B组填料的冻胀变形，同时也降低了其残余变形。闫宏业等[17]、许健等[18]、肖伟[19]、常祥等[20]、岳祖润等[21]利用数值模拟方法研究了保温措施下的路基温度场，研究均表明保温措施可有效减小路基冻结深，用于抑制路基冻胀效果较好。

本文结合兰新高铁高海拔地段气候条件及地质特征，运用ANSYS有限元分析软件，模拟浩门至大梁区间典型断面的路基温度场，分析不同高度路基在冻结过程中温度场的分布规律和变化趋势，研究路基不同深度处铺设保温材料的温度场变化特征，为高寒阴湿地区高速铁路路基冻害防治措施设计提供参考。

1 路基计算模型

兰新高铁浩门至大梁区间位于祁连山南麓，所处地区为门源盆地，处于高寒阴湿环境中。由于高海拔(线路高程为3 000～3 700 m)影响，该地区常年气温较低(年平均气温1.8 ℃)，昼夜温差大。秋季气候阴湿，降雨天数多；冬季气候寒冷(最冷月平均气温-13 ℃)，自每年10月下旬至次年4月下旬长达近6个月的冻结期，为深季节性冻土区。该区间部分段落线路地势低洼，线路周围易积水，下渗至路基中不易排出，导致路基含水率增大，路基在冬季产生冻害现象。发生冻害路基多为零断面换填路基、高度较小的低矮路堤、过渡段及浅路堑等，其中零断面换填路基和低矮路堤处冻害较为典型和普遍，冻害严重、冻胀量大，线路维修工作量大，严重影响轨道的平顺性和列车正常运营。K1 962+618～K1 962+918区段线路高程约为3 500 m，多为零断面换填路基和高度较小的低矮路堤，如图1所示。选取该区段K1 962+618(零断面换填路基)、K1 962+840(路基高度为1 m的低路基)和K1 962+918(路基高度为2 m的低路基)3处典型断面进行路基温度场数值计算，研究冬季路基温度场及其冻结深度的变化规律。

图1 K1962+618～K1962+918处路基

高速铁路路基可视为线性土工结构物，在纵向上假设为无限延伸，路基各土层各向同性且分布均匀，模拟计算时简化为二维平面问题处理。零断面换填路基、1 m和2 m高度的低矮路基计算结构层如图2所示。

图2 路基断面示意(单位：m)

2 土体参数和边界条件

2.1 土体参数

位于季节性冻土区的路基土体在冻融循环过程中，土体骨架和介质水会产生热量传递，而冰水相变会与周围环境进行能量交换，未冻水含量随温度变化，参照文献[13，17-19]采用显热容法将相变潜热的影响等效为比热容的变化，进行简化计算，忽略热流率条件、对流条件和热生成率等条件，主要考虑在外界大气温度的变化下，路基中不同深度处的温度变化。

根据试验资料及相关参考文献，计算模型中各结构层的热物理参数见表1。

表1 计算参数

注：ρd为土体干密度，kg/m3；λ为导热系数，kJ/(m·℃·d)；C为比热，kJ/(kg·℃)。

由于外界温度时刻变化，土的导热系数和比热容都是变化的，为了计算方便，季节性冻土区各土层冻结和融化时的计算参数分别取为常数。在计算中不考虑土体中水分迁移。

2.2 边界条件及初始条件

本文在计算路基温度场中主要采用常用的第一类热学边界条件。所建路基的有限元模型中边界条件分别为：左右边界条件、上边界条件和下边界条件。

根据路基所处地区2016-10-7至2017-11-7气象观测资料(图3)及附面层原理[5]，考虑温度的变化及增温速率的不同，平均增温率取值为0.03 ℃/a。同时结合并应用气象学中的下附面层原理，得出计算区域由于环境温度变化而形成的上边界温度条件，可表述成如下函数形式

式中，Tα为当地初始年平均气温，取值为-1.36 ℃；ΔTc取值为0.03 ℃；A为日平均气温的年振幅，取值为12 ℃；α取值为11π/12；ΔTF取值为3 ℃。

图3 实测气温与拟合气温

计算模型左右边界的温度梯度为零，即两侧绝缘。季节性冻土区，土层的地温变化幅度随着深度的增加而衰减，当达到某一深度即地温年变化深度及以下时，土体的竖向热交换较少，地温基本保持不变，热流条件可忽略不计。结合实测资料和设计资料，该地区地层10 m以下地温基本保持不变，故模型底部下边界条件近似取为常量8.5 ℃。将牛富俊等[2]实测所得2016年3月1日的各土层地温进行稳态计算得到初始条件。由于上边界条件式(1)中计算日期始于2016年10月7日，为计算准确，故将计算日期推至2016年3月2日。

3 路基温度场有限元模型

考虑路基温度场是随空间和时间变化的二维变系数问题，采用有限元和有限差分相结合的混合解法。求解从初始路基温度场开始，在间隔一定的时间步长后，下一阶段对应的路基温度场。

采用ANSYS有限元分析软件来求解路基的温度场，使用平面4节点来划分路基模型单元网格。定义不同结构层材料属性，在分析区域的边界上施加边界条件。由于温度荷载是随时间变化的，将时间-温度曲线离散为荷载步，每1荷载步为1d，进行逐步计算。为精确计算将零断面路基侧沟周围和基床表层及边坡以三角形单元进行划分[12]。路基计算模型的单元长度0.2 m，零断面路基模型共有10 732个节点，10 968个单元；1 m高低矮路基模型共有12 623节点，12 490个单元；2 m高低矮路基模型共有11 403节点，11 282个单元。通过比较冬季各月份的地温曲线分布图对计算结果进行分析。

4 温度场数值计算结果分析

通过对零断面路基、低矮路堤进行温度场模拟，分析其温度场变化规律。对零断面路基不同深度处铺设热阻大、隔热性能良好的XPS保温板的路基温度场进行模拟分析，并与未铺设保温板的路基温度场、冻结深度进行对比，研究XPS保温板对路基的保温效果，为该类路基防冻胀设计提供依据。

4.1 零断面路基冬季实测地温与计算地温对比分析

2015年6月13日～2016年3月1日K1962+618路肩实测地温[2]如图4所示。表2给出了路肩实测冻结深度。

图4 各深度处日平均地温随时间变化曲线

日期冻结深度/cm2015-12-01852016-01-011502016-01-211802016-01-281852016-02-052102016-02-132202016-03-01250

由实测地温可知，路基不同深度处的地温总体呈季节性变化，距离地表越近受外界环境、气温影响越大；随着深度的增加，影响变小，温度-时间曲线趋于光滑。入冬后随着时间增加，冻结深度逐渐加大，2016年3月1日冻结深度达到250 cm。

对K1962+618路基断面处温度场进行数值模拟分析，所得2016年12月到2017年4月路基在不同月份的温度场如图5所示。

图5 K1962+618路基断面处温度场

由图5知，自2016年10月7日该地区进入冬季，随着时间推移，外界温度逐渐降低，路基和周围土体的冻结线逐渐下移，直至达到最大冻结深度；在路基冻结期间，可以看出0 ℃线总体呈“凸”形。路基不同部位冻结深度随时间变化见表3，各处最大冻结深度及发生时间见表4。

表3计算结果与实测结果基本一致，说明计算模型、参数等取值合理，可以为其他相同条件断面数值模拟分析采用。入冬后随着时间增加，气温持续降低，冷量不断输入路基中，各部位冻结深度持续增大。由图5知，零断面路基冻结初期受侧沟影响，使坡脚处于多向冻结状态，其冻结深度大于天然土壤、线路中心、轨道中心的冻结深度。到3月底或4月中上旬路基及周围天然土壤陆续达到季节最大冻结深度；天然土壤、坡脚处分别于3月30日、3月25日达到最大冻结深度2.40，2.60 m；路肩处于4月4日达到最大冻结深度为2.70 m；轨道中心处、线路中心分别于4月12日达到最大冻结深度2.41，2.31 m；与2015年～2016年实测冻结深度基本一致。路基两侧天然土壤的冻结深度和路基中心线处的冻结深度相差不大；路肩处冻结深度最大。

表3 路基不同部位冻结深度随时间变化

表4 各处最大冻结深度及发生时间

由表2实测和表4计算结果可知：浩门—大梁区间路基冬季冻结深度较大，普遍在2.3～3.0 m，达到最大冻结深度时间和解冻时间较晚，这与该区间线路高海拔，冬季冻结时间长且气温低有关。

4.2 设置保温层的零断面路基温度场

参照有关文献中的研究，对路基面下深40 cm或80 cm处铺设厚0.1 m、宽14.4 m的XPS保温板进行数值模拟分析(图6、图7)，图中粗黑线为保温板。

(1)40 cm深处铺设XPS保温板温度场分析

图6给出了在路基面下40 cm深处铺设XPS保温板2017年4月1日路基温度场分布情况。表5给出了轨道中心线、线路中心线下冻结深度随时间变化计算结果。

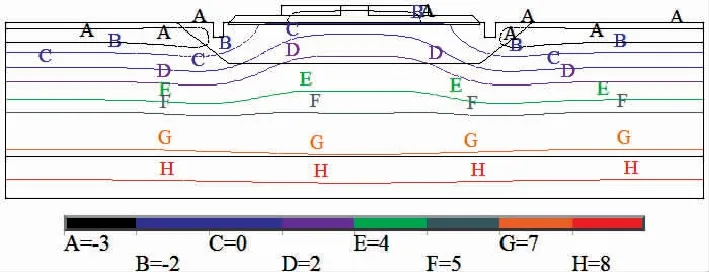
图6 铺设XPS保温板路基温度场(40 cm)

日期轨道中心/m线路中心/m2016-12-010.470.462017-01-010.500.492017-02-010.780.782017-03-011.031.012017-04-011.081.02最大冻结深度1.101.10

从上述计算结果可知，在冻结初期，铺设保温板的路基冻结深度与未设保温板的冻结深度相差不大；之后随着冻结时间增加，铺保温板的路基冻结深度不断加大，但冻结深度及冻结速率远小于未铺设保温层的路基；轨道中心线下与线路中心线下最大冻结深度均为1.10 m，远小于未铺设保温材料的路基冻结深度(2.41，2.31 m)。由此可见，铺设保温材料可以大幅度减小路基冻深，改善路基温度场，路基冻害防治效果十分明显。

(2)80 cm深处铺设XPS保温板温度场分析

图7给出了在路基面下80 cm处铺设XPS保温板2017年4月1日路基温度场的分布情况。表6给出了轨道中心线和线路中心线下冻结深度随时间变化的计算结果。

图7 铺设XPS保温板路基温度场(80 cm)

日期轨道中心/m线路中心/m2016-12-010.840.832017-01-010.880.882017-02-010.900.902017-03-011.161.102017-04-011.191.15最大冻结深度1.201.20

当保温板铺设位置加深时，在冻结前期路基冻结深度与未铺设的相同。随着冻结时间增加冻结深度也增大；但当冻结深度超过80 cm后，由于保温板的存在使得冻结速率显著减小；路基面下80 cm处铺设保温材料时轨道中心线下与线路中心线下最大冻结深度均为1.20 m，略大于在路基面下40 cm深处铺设保温板的值，同样小于未铺设保温材料的路基冻结深度(2.41，2.31 m)。在路基面下40 cm处铺保温板保温效果较路基面下80 cm处好。

4.3 低矮路堤冬季路基温度场分析结果

图8、图9给出了路基高度(h)为1 m、2 m的低路堤典型断面温度场2017年4月1日的数值模拟分析结果。表7、表8给出了不同时间的路堤冻结深度、最大冻结深度及发生时间。

图8 低路堤温度场(h=1 m)

图9 低路堤温度场(h=2 m)

日期轨道中心/m线路中心/m2016-12-010.600.542017-01-011.301.232017-02-011.891.812017-03-012.322.222017-04-012.612.51最大冻结深度/m2.702.61发生时间2017-04-202017-04-21

表8 低路堤冻结深度(h=2 m)

低路堤和零断面路基温度场分布规律除路基边坡附近外基本相同。高度1 m路基轨道中心处和线路中心处最大冻结深度分别为2.7，2.61 m，发生时间分别为2017-04-20、2017-04-21；高度2 m路基轨道中心处和线路中心处最大冻结深度分别为2.61，2.52 m，发生时间分别为2017-04-19、2017-04-18；两处低路堤最大冻结深度均大于零断面换填路基最大冻结深度，且发生时间略晚一些，这与路基基床以下部位土层性质、厚度、热物性参数和地温年变化深度线距离路基顶面的高度等有关。

5 结论

通过对兰新高铁高寒区浩门至大梁区间典型断面路基温度场数值模拟及实测数据对比分析，以及对不同深度处铺设保温材料路基温度场变化特征研究，得出以下结论及建议。

(1)实测数据及数值模拟结果表明：由于兰新高铁浩门至大梁区间海拔高、冬季冻结时间长、气温低等原因，导致该区间路基冻结深度普遍较大(2.3～3.0 m)，达到最大冻结深度时间和解冻时间较晚。

(2)零断面换填路基实测地温和数值模拟计算结果基本相符；计算模型、参数等取值合理，可以为其他相同条件断面数值模拟分析采用。实测及计算结果可为同类条件下的高速铁路路基防冻胀设计参考。

(3)在路基面下40 cm和80 cm处铺设保温板路基温度场较未铺设保温板的0 ℃线上移，冻结深度增加速率变小，最大冻结深度明显减小，受气温影响变小，保温效果好。40 cm处铺设保温板较80 cm处铺设保温板冻结深度小，保温效果更好。

(4)路基高度为1 m和2 m的路堤温度场变化规律与零断面换填路基温度场变化规律基本一致。由于路堤边坡、基床以下部位土层性质、厚度、热物性参数等影响，低路堤最大冻结深度比零断面换填路基的大。