嵌入式反压护道作用下软基路堤稳定性研究

何 杰

(中铁四局集团有限公司设计研究院,安徽 合肥 230022)

0 引言

在近海岸、河口三角洲及山区沟谷等地区存在有大量的软土,该类土具有大孔隙、高含水量、高压缩性、强度低等特性。在该类软土地基上修筑高填路堤,势必会引起路堤产生较大沉降或不均匀沉降。若填土产生的附加压力超过软土地基的承载力,则会导致路堤失稳发生滑动。因此对于软土路基上修筑高路堤时都要采取加固处理措施。

对于软基路堤的加固主要有2种措施:① 改善软土地基的物理力学性质,如预压法、碎石桩法、CFG桩法、水泥土搅拌桩等;② 基于边坡的滑动机理提高抗滑力的措施,如反压护道。反压护道是在路堤两侧填筑一定高度与宽度的土体,高度一般不大于路堤填筑高度的1/2,在土体的自重作用下改善路堤荷载,使软土地基侧向隆起的趋势得到抑制,从而提高路堤边坡的稳定性。

目前常采用极限平衡法对反压护道作用下的软基路堤稳定性进行分析。文献[1]基于极限平衡理论,建立了嵌入式反压护道作用下软基路堤稳定性的极限平衡方程,并给出软土地基上路堤填筑极限高度的解析解;文献[2]采用极限平衡法对反压护道加固的金宜公路钱资荡软基段进行分析,确定了路堤的填筑高度与填筑速率。随着计算机技术的不断进步与土体本构模型的不断发展,数值分析方法得到了广泛应用,并愈发成熟。数值分析方法具有自动化、可视化程度高、模型清晰、无需像极限平衡法预先假定滑动面形状及位置、理论严密等特点，因此许多学者在反压护道数值分析方面做了大量的研究。文献[3]在考虑土体非线性的基础上,利用ANSYS有限元软件对软土地基上填筑高路堤的变形性状进行分析,预测路堤的沉降量;文献[4]提出三维有限元数值方法,结合四川省遂宁-资阳-眉山高速公路的软基监测项目,利用FLAC软件针对典型路段路堤进行三维有限元分析;文献[5]通过有限元软件分析反压护道加固软基路堤机理,结果表明反压护道有助于减小路堤的侧向位移。

目前学者们对反压护道作用的软基路堤开展了较多研究,并取得一定的成果[6-11]。在反压护道应用实践中,也出现一些新的问题,如由于反压护道占地面积大,在有些路段不存在建设空间,无法采用反压护道方法加固地基。针对此问题,本文提出利用嵌入式反压护道对软土地基进行加固,采用数值模拟方法验证嵌入式反压护道的可行性,分析嵌入式反压护道宽度和高度对软基路堤稳定性影响,并探讨了嵌入式反压护道加固软弱地基的机理。本文研究结果对推广应用嵌入式反压护道法、节约建筑场地、保护环境具有重要意义。

1 工程背景

某高速公路软弱路基位于某岛屿上,水资源丰富,地基含水量高。路基顶面宽度为33 m,高度为6 m,坡度为1.0∶1.5。道路一侧为大规模海产养殖场,从保护养殖户利益和保护环境角度出发,不易大规模征用养殖户土地。于是采用嵌入式反压护道,将反压护道体埋入地下既可以保证路堤稳定,又可以节省一些土地,嵌入式反压护道加固软基剖面图如图1所示。

图1 嵌入式反压护道加固软基剖面图

2 数值模型的建立

为了揭示嵌入式反压护道对路堤稳定性的影响,利用FLAC3D建立软基上路堤数值分析模型。数值计算模型分3个部分,上面为路堤,下面为软土地基。路堤顶面宽度方向尺寸为33 m,高度方向尺寸为6 m,路堤坡比为1.0∶1.5;软土地基的高度方向尺寸为20 m,宽度方向尺寸为91 m；反压护道嵌入到软土路基中,具体模型如图2所示。

图2 数值计算模型

软土路基部分X、Y、Z方向单元长均为1.00 m,3个方向分别有91、1、20个单元,整个软土地基单元总数量为1 820个;路堤部分X、Y、Z方向单元长均为1.00 m,3个方向分别有51、1、6个单元,整个路堤模型单元总数量为306个。

采用齐次边界条件,沿整个模型纵向前后2个截面土体沿Y向位移固定,软土左右截面土体X向位移固定,软土下部边界X、Y、Z向位移固定,模型的其余边界取自由面。各土层模型采用摩尔-库伦本构模型。

根据中铁四局集团有限公司设计研究院提供的工程资料可得填土与软土的物理参数,填土路堤重度γ=19 kN/m3,变形模量E=20 MPa,泊松比ν=0.30,内摩擦角φ=24°,黏聚力c=20 kPa;软土地基重度γ=17 kN/m3,变形模量E=5 MPa,泊松比ν=0.35,内摩擦角φ=6°,黏聚力c=8 kPa。路堤两侧的嵌入式反压护道采用与路堤填土相同的材料。

3 模拟方案

对于嵌入式反压护道处理的软基路堤,护道宽度B和高度H是控制软基路堤稳定性的重要因素。为了进一步揭示嵌入式反压护道参数对路堤稳定性的影响规律,本文分析不同护道参数下的路堤稳定性。先开展在没有反压护道的情况下路堤稳定性数值计算,再分别取嵌入式反压护道高度3、4、5、6 m,分析护道高度对路堤稳定性影响;分别取嵌入式反压护道宽度5.0、7.5、10.0 m,分析护道宽度对路堤稳定性影响。每个嵌入式反压护道高度和宽度分别组合,计算不同工况下路堤稳定性系数。采用强度折减法计算路堤稳定系数。

4 计算结果与分析

4.1 嵌入式反压护道加固效果分析

未经加固地基模型中剪应变增量云图如图3所示。

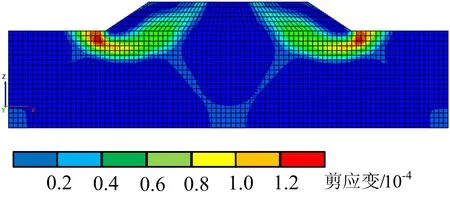
图3 未经加固地基模型中剪应变增量云图

从图3可以看出，滑动面从路堤顶面贯通到软基面,路基发生滑动破坏。采用强度折减法得路堤稳定性系数仅为1.03。由此可知,若不加固,路堤处于临界状态,则在外界扰动作用下易发生失稳。

根据文献[12]可知本工程边坡安全系数为1.2。本文研究护道高度H为3、4、5、6 m共4种工况下,路堤边坡稳定性系数随护道宽度B的变化情况,如图4所示。

从图4可以看出,不同工况条件下,路堤边坡稳定性系数均大于未施加嵌入式反压护道路堤边坡的稳定性系数(FS=1.03)。护道宽度B=10.0 m、高度H=6 m的路堤边坡稳定性系数比未施加护道的稳定性系数增加22.33%,说明嵌入式反压护道对提高软基路堤稳定性有明显的作用。

图4 不同护道加固宽度对路堤稳定性系数的影响

4.2 嵌入式反压护道尺寸对路堤稳定性的影响

对比分析图4中不同高度反压护道发现，路堤边坡的稳定性系数随着护道宽度的增加而增大,增大幅度近似于线性。通过线性拟合计算,得出路堤边坡稳定性系数与护道宽度拟合关系，见表1所列。

表1 路堤边坡稳定性系数与护道宽度拟合关系

由表1可知,随着护道宽度的增加,路堤边坡稳定性系数呈线性增长;随着高度增加增长幅度逐渐增大。

不同护道宽度下,路堤边坡稳定性系数随护道高度的变化如图5所示。从图5可以看出,路堤边坡稳定性系数随着护道高度的增加而逐渐增大,同样近似于线性增大。

图5 不同护道加固高度对路堤稳定性系数的影响

通过线性拟合计算,得出路堤边坡稳定系数与护道高度拟合关系，见表2所列。

从表2可以看出,路堤边坡稳定性系数随护道高度的增加而增大,增大幅度随着护道宽度增加而增大。

表2 路堤边坡稳定性系数与护道高度拟合关系

对比表1、表2可知,随着护道宽度增加稳定性系数增加幅度大于随着护道高度增加稳定性系数增加幅度。由此可知,护道宽度对路堤稳定性系数影响更大。

综上所述,采用嵌入式反压护道加固软基路堤时,宽度越大对路堤的稳定性越有利;同样高度越大对路堤稳定性越有利。护道宽度对路堤稳定性系数影响更大。

4.3 嵌入式反压互道加固路堤最大剪应力分析

为了揭示嵌入式反压护道加固软基路堤机理,本文对路堤最大剪应力分布进行研究。当B=7.5 m时,不同高度护道软基路堤模型中最大剪应力分布云图如图6所示。

从图6可以看出,H为3、4、5 m时,嵌入式反压护道时路堤剪应力最大值为41.3、37.0、30.5 kPa。由此可知,随着护道高度的增加,路堤中最大剪应力逐渐减小。

图6 不同高度护道软基路堤最大剪应力分布云图

嵌入式反压护道可以在一定程度上减小路堤中剪应力,改变了路堤土体局部应力状态,从而增加了稳定性系数。

5 路堤极限高度分析

护道宽度B=7.5 m、高度H=5 m时,路堤边坡稳定性系数为1.22,满足稳定性要求,实际工程中可以将嵌入式反压护道设计为护道宽度B=7.5 m、高度H=5 m。对于软土地基上的填方路堤,一般采用路堤填土极限高度来控制其稳定性。为了计算嵌入式反压护道作用下软基路堤的极限高度,本文针对上述算例开展了护道宽度B=7.5 m、高度H=5 m工况下,不同高度路堤边坡稳定性系数的对比分析。通过计算可知,当路堤高度H′=6 m时,FS=1.200;当H′=8 m时,FS=1.061;当H′=8.5 m时,FS=1.018;当H′=9 m时,FS=0.982。当FS=1.0时,对应的路堤极限高度约为8.75 m,即当路堤高度填筑到8.75 m时,将发生失稳滑动。

在传统极限平衡法中,嵌入式反压护道作用下路堤的极限高度公式[1]如下:

(1)

Nq=tan(45°+φ/2)etan φ

(2)

Nc=(Nq-1)ctanφ

(3)

6 结论

本文提出采用嵌入式反压路堤加固软基路堤,并采用数值模拟方法和理论分析方法,针对典型工程案例进行研究,分析嵌入式路堤作用下软基路堤的稳定性和极限高度,得出如下结论。

(1) 嵌入式反压护道能够显著提高路堤边坡稳定性,对加固软基路堤边坡是有效的。

(2) 随着护道宽度的增加,路堤边坡稳定性系数逐渐增长;随着高度增加增长幅度逐渐增大。随护道高度的增加,路堤边坡稳定性系数同样近似于线性增大,增大幅度随着护道宽度增加而增大。

(3) 软基路堤边坡稳定系数随着护道宽度增加而增加幅度大于随着护道高度增加而增加幅度,即护道宽度对路堤稳定性系数影响更大。

(4) 设置嵌入式反压护道可以在一定程度上减小和改善软基路堤土体的应力状态,尤其减小局部土体剪切程度,从而改变路堤稳定性系数。

(5) 通过数值计算获得的反压护道作用下软基路堤边坡的极限高度与极限平衡法获得的解析解几乎吻合,表明可以采用极限平衡法对嵌入式反压护道破坏路堤稳定性进行计算和设计。