桥上有砟轨道无缝道岔非线性阻力及其影响分析

李少铮,韦安祺,陈嘉胤,刘 浩,王 平,肖杰灵

(1.西南交通大学高速铁路线路工程教育部重点实验室,成都 610031； 2.西南交通大学土木工程学院,成都 610031)

桥上无缝道岔是高速铁路发展建设中铺设跨区间无缝线路不可避免的技术难题。高速铁路无缝道岔具有保证列车平稳、安全运行，提升旅客乘车舒适感，延长线路设备的使用寿命等显著优点[1]，但由于其本身结构和下部基础的复杂多样性，桥上无缝道岔在有砟道床上的铺设一直是铁道科研工作者研究的重点和难点之一。无缝道岔对线路纵向阻力具有很高的敏感性，过量的钢轨附加纵向力及其变形易于丧失无缝道岔的几何平顺性并导致其结构部件的破损[2]。在钢轨纵向力分布及位移分析过程中，参数的合理取值(尤其是道床阻力)是非常重要的，实测线路的纵向阻力-位移曲线表现为幂指数非线性形式[3]。而目前规范[4]将线路纵向阻力值简化为理想的弹塑性阻力取值。采用实测的非线性阻力形式更为接近实际，且考虑阻力非线性变化的无缝道岔阻力特性研究具有十分重要的意义。

近年来跨区间无缝线路技术的相关关键技术不断发展。在道床纵向阻力的测试方面，由于道床的散粒体[5-8]及流变特性[9-10]，道床纵向阻力的测试结果不具有重复性，因此各国学者往往采用统计学方法进行道床纵向阻力研究。此外，关于扣件系统阻力取值的相关问题，也被大家所广泛关注[11-15]。无缝道岔的相关计算理论及方法也在不断完善[16]。王平等[17]探讨了在长大桥梁上无缝道岔的布置方式与伸缩调节器之间的相互影响。杨荣山等[18]根据桥上无缝道岔受力和变形特点，建立道岔-桥梁-墩台一体化计算模型，计算得出桥上无缝线路与桥上无缝道岔的受力和变形差别很大。高亮等[19]从温度荷载、竖向荷载、钢轨横向变形等方面对空间力学特性进行了分析。通过分析列车荷载的影响，得出半联满布荷载下的钢轨挠曲附加力和纵向位移最大。

本文采用试验与理论相结合的方法，进行基于非线性和弹塑性阻力特性的高速铁路无缝道岔状态演变参数试验和仿真分析研究。在室内进行扣件反复加卸载及道床反复推拉试验，分析其纵向阻力的弹塑性变化特性，并提出在重复加载作用下纵向阻力表达式。理论分析阶段则是根据试验研究获得的阻力特征曲线，构建无缝道岔新型线路阻力本构模型，开展实测非线性阻力参数模型与规范阻力参数模型的对比分析。以期对桥上无缝道岔的设计与工程应用提供指导。

1 无缝道岔非线性阻力参数试验

1.1 试验方案

1.1.1 试验材料及设备

为了得到多次荷载作用下线路纵向阻力的弹塑性变化特征，通过建立室内足尺有砟轨道模型[20]。在室内分别进行扣件反复加卸载和道床纵向阻力测试试验，获取扣件纵向阻力和道床纵向阻力。

本次道床阻力试验采用现场使用的一级道砟，使堆积形成的道砟级配满足规范要求[21]。本次试验采用的道砟级配如图1所示。扣件加卸载试验采用60 kg/m钢轨和弹条II型扣件进行测试。

图1 道砟粒径级配

1.1.2 试验原理及方法

扣件反复加卸载纵向阻力测试如图2(a)所示：千斤顶的加载位置为钢轨轨底处，在被测钢轨的另一端安装百分表。施加纵向力，记录百分表的读数，读取钢轨纵向位移值。加载时采用分级加载的方式，速度为1 kN/min，每加一级荷载时保持30 s，待百分表示数稳定后再读数，阻力值开始滑移或者钢轨位移达到4 mm时停止加载，此时开始卸载，待百分表读数稳定后记录钢轨位移残余变形值，记录荷载-位移值并绘制扣件阻力-位移关系曲线。

道床纵向阻力测试原理如图2(b)所示。加载时使千斤顶的加载方向垂直于轨枕，且位于轨枕中部偏下，在被测轨枕的另一侧两端对称安装百分表。试验开始后，施加纵向力，读取并采集百分表的读数，取两百分表的位移均值作为轨枕位移值。加载时采用分级加载的方式，加载速度为1 kN/min，每加一级荷载时保持30 s，待百分表示数稳定后再读数，阻力值开始滑移或道床位移达到6 mm左右时停止加载，此时开始卸载并记录轨枕位移残余变形量，视为初值加载。当全部卸荷完毕后，将千斤顶放置在轨枕另一侧开始反向加载。最后，再将千斤顶放置在和初值加载相同的位置，进行与初值加载方向相同的再加载。如此往复多次，记录轨枕位移阻力值。

图2 线路纵向阻力测试原理

1.2 试验结果及分析

为得出钢轨回弹位移量与位移值的关系，绘出如图3所示的循环荷载作用下的钢轨位移曲线。

图3 180 N·m扣件扭矩下累计位移曲线

由图3可知，钢轨纵向位移的卸载曲线与加载曲线基本吻合，表现出较强的规律性。可以认为在纵向阻力作用下，钢轨在滑移前的位移-阻力曲线表现出弹性特征，且曲线斜率与卸载的一致。试验最后进行一次性卸载，待位移值稳定后进行读数，可以发现各组卸载曲线基本平行，说明在相同加载条件下，钢轨位移回弹量与钢轨最终位移值无关。

图4为试验得到的道床阻力以及扣件系统纵向阻力-纵向位移曲线。为了分析加载历史的影响并减少单次试验的误差，将多次测得的加载数据进行综合指数拟合，并与初次加载后的阻力-位移拟合曲线进行对比分析。根据试验数据，对道床纵向阻力进行曲线拟合分析。

图4 线路纵向阻力拟合曲线

从图4(a)可以看出，进行多次重复加载试验后，钢轨产生位移的线弹性区间变小。分析认为，反复加载试验后，一方面钢轨存在残余变形，胶垫可提供的变形量变小，另一方面，胶垫存在蹿出的情况，这两种因素共同导致钢轨滑移的提前出现。由图4(b)可知，道床纵向阻力随着加载次数的增加存在小幅度增加，经过挤压后道床散粒体结构变得更加密实。

2 岔-桥-墩一体化连续梁模型

为了得到无缝道岔在考虑了非线性的参数及道床阻力的情况下的相关力学参数。在ANSYS中建立4×32 m岔-桥-墩一体化连续梁模型，将道岔和桥梁作为一个相互作用、相互影响的耦合系统，基于非线性有限单元法[22]建立岔-桥-墩连续梁模型。图5为岔-桥-墩一体化有限元模型。

进行考虑纵向阻力弹塑性影响的仿真分析。为消除边界效应，在连续梁两侧各构建两跨32 m简支梁模型，并考虑100 m的路基段，道岔布置位置如图6所示。

图5 岔-桥-墩一体化有限元模型

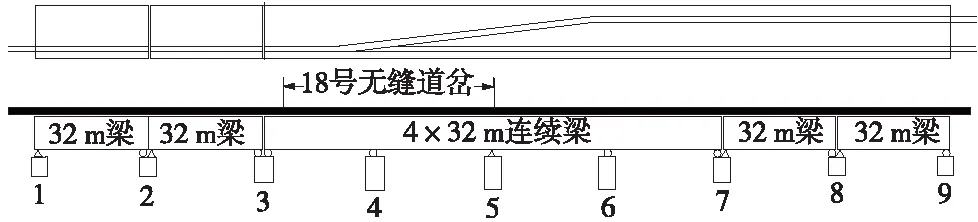
图6 岔-桥-墩一体化四跨简支梁模型

岔-桥-墩一体化有限元模型采用杆单元模拟钢轨，梁单元模拟桥梁和轨枕，非线性弹簧单元模拟钢轨和道床的纵向阻力、限位器和桥墩刚度，线性弹簧模拟间隔铁。采用60 kg/m钢轨，18号可动心轨无缝道岔，弹条Ⅱ型扣件，Ⅲ型混凝土枕，尖轨跟端设置1组限位器，心轨跟端与翼轨间设置4组间隔铁。道岔限位器采用分段线性阻力，限位器子母块间隙取值7 mm，当限位器子母块贴靠，两轨相对位移小于1 mm时，限位器阻力取值为1.5×105kN/m；当两轨相对位移大于1 mm时，限位器阻力取值6×104kN/m。道岔间隔铁阻力采用线性阻力，取值为5×104kN/m。桥梁为C40混凝土连续梁桥，两侧简支梁桥墩的刚度为1×105kN/m，中间固定墩桥墩刚度为5×105kN/m，有砟轨道轨枕间距为0.6 m。试验中线路纵向阻力参数取值如表1所示。

表1 线路纵向阻力取值

注：R为线路纵向阻力；x为轨枕相对纵向位移，mm。

3 温度变化对无缝道岔的影响

分别进行梁体升温15 ℃，钢轨升温0 ℃，30 ℃，40 ℃和50 ℃时的伸缩附加力工况和考虑中-活载作用下的牵引/制动工况仿真分析。并提取桥梁与道岔的受力变形参数进行阻力取值影响的对比分析。使用多段线近似模拟实际线路纵向阻力的变化趋势，如图7所示。

图7 线路纵向阻力取值

图8 伸缩附加力工况下直基本轨受力

从图8可以看出，升温工况下峰值附近的无缝线路岔区的直基本轨纵向力要高于非岔区以及路基段钢轨应力，且岔区段钢轨主要受拉，非岔区地段钢轨应力主要受压。同侧三跨简支梁梁缝处的温度应力值相近，并从岔区向路基方向逐渐递减。从总体看，左侧简支梁梁缝处的温度应力要大于右侧，这种差距随着钢轨温度的升高越来越明显。在钢轨升温40 ℃工况下，限位器开始贴靠并传力，此时钢轨最大应力位置开始出现在限位器附近。

同时，当钢轨温升较低，梁轨相对位移较小时，采用规范值计算所得的直基本轨拉压应力大于采用试验值所得的钢轨拉压应力，这种现象随着钢轨温度的升高渐渐减弱，并最终在钢轨升温达到50 ℃时，二者所得的直基本轨附加力曲线基本重合。当钢轨温度较低时，两种参数计算结果差异较大，最终表现为在两种计算结果下直基本轨受力差异。但随着升温幅度增大，梁轨间相对位移逐渐变大，二者间的差异也在逐渐减小。

在研究纵向阻力取值对牵引/制动附加力的影响时，按文献[4]规定的方法进行计算，Qd取中-活载加载模式，轮轨黏着系数μ取0.164，Q=μ×Qd。加载方式如图9所示。

图9 牵引/制动附加力加载模式

图10 牵引/制动工况下梁轨相对位移

图10为牵引/制动工况下的梁轨相对位移。在考虑中-活载的牵引/制动工况下，连续梁固定支座的右侧大部分区域的梁轨相对位移已经超出4.5 mm，可以近似认为，在连续梁固定墩的右侧的部分线路上，采用非线性阻力参数计算时梁轨相对位移较大，故而常规计算时采用规范值计算偏于不安全。

由图11可知，试验值所对应的直基本轨所受拉压附加力都要大于规范值所对应的钢轨拉压附加应力，且这种差异在固定墩的右侧的桥上线路段表现得更为明显。

图12为牵引/制动工况下直基本轨位移，由图12可以看出，试验值对用的直基本轨位移在固定支座的右侧要大于试验值对用的基本轨位移。

图11 牵引/制动工况下直基本轨受力曲线

表2为各个工况下的无缝道岔受力与变形对比。与采用非线性线路纵向阻力相比，采用线性规范值进行无缝道岔的受力分析，会使钢轨应力和位移普遍偏小。升温幅度较低时，二者的计算偏差不能忽视。以钢轨升温30 ℃为例，采用规范值计算所得的直基本轨的附加温度力与实际值相比小32.7 kN，偏差达到15%。在考虑牵引/制动附加力时，这种偏差可以达到9.3 kN，使用规范阻力值计算所得与实际测试值相比偏小约9%，说明在阻力强化区段使用规范阻力值进行取值计算偏于不安全。限位器开始贴合传力后，二者计算所得的间隔铁与限位器受力也存在一定偏差，应用非线性阻力取值计算下的限位器和间隔铁最大作用力要高于使用规范取值时的计算数值。

图12 牵引/制动工况下直基本轨位移

表2 线路阻力不同时无缝道岔受力与变形比较

4 结论

本文分析了无缝道岔在考虑非线性参数及道床阻力的情况下的相关力学行为，采用试验手段建立有砟道床足尺模型，在考虑参数非线性的条件下建立岔-桥-墩一体化连续梁模型有限元模型，并分析了温度变化对无缝道岔的影响，主要结论如下。

(1)当梁轨相对纵向位移不太大时(本次试验为0～4.5 mm)，使用规范规定的线路纵向阻力进行高速铁路桥上无缝道岔受力与变形分析，会使计算结果与实际相比普遍偏小，本试验中伸缩附加力工况和牵引、制动工况下的最大直基本轨附加温度力偏差分别达到15%和9%。

(2)随着温度的上升，梁轨相对位移变大，规范值与实测值的线路纵向阻力差异开始变小，使用规范值计算所得的直基本轨和限位器、间隔铁的受力也逐渐逼近实际值。

(3)在阻力强化较为明显的情况下，简单采用规范值进行设计计算会使得计算结果偏于不安全，在工程中应尽量进行大量的试验分析，从而修正规范值。