地下水路堑段槽型挡土墙设计若干问题的探讨

孙东泽

(中铁工程设计咨询集团有限公司,北京 100055)

1 概述

为简化计算，一般将槽型挡土墙边墙和底板分开按不同构件类型设计：边墙简化为固定在底板上的悬臂梁，底板简化为支承于地基上的梁—弹性地基梁[1-3]。边墙的受力状态比较明确，简化为悬臂梁较为合理；底板受力状态较为复杂，在特定条件下，边墙外部土体会对底板梁端转动位移形成约束，弹性地基梁模型存在缺陷。

对于作用在边墙上的土压力，多数设计人员认为：一般按主动土压力计算，但边墙刚度较大时，如果墙顶的水平位移小于产生主动土压力所需的位移时，应按静止土压力计算。静止还是主动，欧洲和加拿大的岩土工程标准[4-5]对此给出了明确的位移限值(表1)，我国规范没有相关规定。

对于槽型挡土墙底板来说，基本可变荷载或者说主要可变荷载一般指槽内车辆荷载，对于边墙来说，其外侧的车辆或人群是其基本可变荷载。问题是，底板结构计算时，边墙基本可变荷载引起的内力如何参与荷载组合，公路、铁路规范中都未明确[6-7]。

除前述几个问题外，槽型挡土墙还存在抗浮安全系数取值、地基刚度参数确定等问题，本文将就此展开讨论，并尝试提出改进建议。

表1 发挥土压力所需的位移值

注：H为墙高，m。

2 槽型支挡结构不同工况受力分析

拟定基准路堑式槽型支挡结构：边墙净高6 m，槽净宽12 m，边墙及底板厚度均采用0.8 m，地下高水位与墙顶齐平，墙外活荷载按15 kN/m2考虑，槽内轨道列车荷载按160 km/h城际铁路取用。针对不同工况，按悬臂梁+弹性地基梁模型分别计算其内力及位移，弹性地基梁计算采用链杆法[8]，计算结果见表2。表2中内力、链杆力均为标准值，边墙弯矩以墙外侧受拉为正，底板弯矩以板底受拉为正。

表2 不同工况内力及位移

注：H为边墙净高，m。

(1)在1号工况条件下，由于水压力较大，底板中部出现较大负弯矩(图1)，位于两个边墙之间的弹性地基梁链杆出现负反力，且越靠近梁中点负反力越大。一方面，考虑链杆不能承担负反力，取消产生负反力的链杆，底板中部负弯矩会进一步加大；另一方面，该内力分布情形相应的梁端转角位移使得边墙转而推挤其外侧土体，这种推挤受到限制，反过来约束了地基梁梁端转动，使得底板中部负弯矩减小，端部正弯矩增大。因而，该工况的实际状态是：地基梁梁端地基应力集中，产生较大的向下位移，使得应力迅速重新分布，靠近梁中部可能存在无地基反力区段；边墙对外侧土体的推挤，使得边墙受力大于主动土压力。

因此，实际边墙底部弯矩、底板端部弯矩会较计算值大，底板中部负弯矩会较计算值小。在地下水位较高的情况下，按悬臂梁+弹性地基梁模型计算槽型挡土墙存在缺陷。

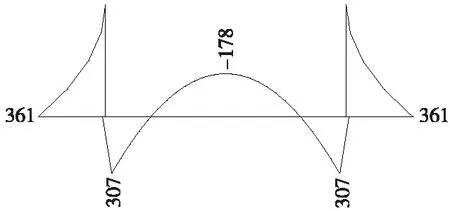
图1 1号工况弯矩(单位：kN·m)

(2)对比2、3号工况，墙外活荷载传递到边墙上的压力、土压力均对底板产生正弯矩，但2号工况底板中部仍然出现负弯矩(图2)，因此，负弯矩主要由边墙自重集中作用于底板端部引起。

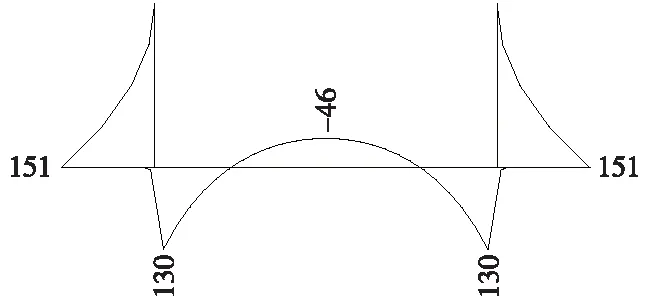
图2 2号工况弯矩(单位：kN·m)

同时，可以看到底板中部的链杆反力仍然是正的。

(3)3、4号工况分别是墙外活荷载、轨道列车荷载单独作用结果。不考虑荷载组合系数，仅简单叠加2、3、4工况，可以看出，底板不再出现负弯矩，链杆也不再出现反力。

(4)各工况条件产生的边墙顶水平位移、转动位移远远小于欧洲及加拿大岩土标准给出的位移限值。

3 关于地下水路堑段槽型挡墙设计的讨论

结合前节受力分析结果，对地下水路堑段槽型挡土墙设计有如下讨论。

3.1 边墙土压力

在地下水位较高且无载工况下，弹性地基梁链杆会出现负反力，暴露出计算模型缺陷的同时，求得的弯矩计算值可能偏小；边墙位移值远远小于欧洲及加拿大岩土标准给出的位移限值，表明一般情况下墙外不产生主动土压力。如改按静止土压力[9-11]计算，边墙底、底板端弯矩将增加30%～40%。

因此，一般情况下墙外土压力按静止土压力考虑更为稳妥。

3.2 地基承载力

由于弹性地基梁模型的局限性，即使不出现链杆负反力，链杆反力也难以反映出应力重分布的影响，有些设计人员以链杆最大正反力来评判地基承载能力甚至作为槽下地基处理的依据，是不恰当的。

因此，对地基承载能力的评价，宜基于结构整体并施加相应荷载，按正常使用极限状态，采用标准组合。

3.3 墙外活载

不论是公路、铁路，目前均将支挡结构上方作用的车辆等活载简化为土柱，连同墙背土体一起计算土压力，按综合作用效应参与组合，采用了相同的分项系数[12-13]，对于路堤支挡结构来说，车辆荷载是主可变荷载，这样处理有其合理性，但对于槽型挡土墙，槽内的车辆荷载是主可变荷载，槽外的活荷载退居其次了，再合并至土压力中就不合理了，也与作用分类、荷载分项系数的概念不协调，易引起设计者概念上的误解。

建议参照德国铁路规范的做法[14-15]，单独计算其侧压力(图3)，或采用弹性理论计算其侧压力，以便于进行不同的荷载组合，考虑不同的分项系数，而且方法明确、概念清晰。

图3 路基面荷载对边墙的侧压力计算图示

3.4 抗浮设计

地下水位较高时，槽型挡土墙存在抗浮稳定问题。

(1)抗浮措施

通常采用加大结构自重、底板向外延伸增加土体配重、设置抗拔桩等方式抗浮[16-17]。水位波动较大时，加大结构自重会对最低水位时的地基承载能力提出额外要求，也不经济；抗拔桩可以满足任何抗浮工况要求且无需改变结构尺寸及轮廓，但抗拔桩的设置导致底板地基刚度突变、底板局部应力集中，不利于承受循环荷载；底板外延利用上部土重抗浮较为经济，也能有效改善边墙下部地基应力集中问题，使底板内力分布更合理，其缺点是基坑偏大易受限于场地条件。底板外延的特殊形式是边墙采用倾斜背坡。

有条件时，优先推荐底板外延方式。采取抗拔桩时，宜设置较大的桩顶托盘或设置纵横向托梁，改善应力集中现象。

(2)关于抗浮系数

地铁规范[18]规定不计地层侧摩阻力时抗浮安全系数不小于1.05；广东省建筑基础设计规范[19]要求：地下室抗浮W/F≥1.05，W为地下室自重及其上作用的永久荷载标准值的总和，F为地下水浮力标准值；水池结构设计规程[20]规定：抗浮稳定验算时作用均取标准值，安全系数不应小于1.05。

参考上述有关规定，建议其抗浮稳定按式(1)验算。

(1)

式中，W为抗浮力标准值；F为浮力标准值；γ0为结构重要性系数(γ0<1.0时取1.0)。

3.5 地基压缩模量

本文进行弹性地基梁计算时，选用的地基变形指标是地基压缩模量。在工程实际中，试验得到的压缩模量值具有一定的离散性，很多设计人员对选取计算用值较为纠结。基于前述2号工况，采用库伦主动土压力，不同地基压缩模量的底板受力(标准值)见表3。

表3 不同地基压缩模量的底板受力对比

在压缩模量由4 MPa逐渐增大到40 MPa的过程中，底板跨中负弯矩由51.9 kN·m逐渐减小到41.3 kN·m，但端部弯矩及链杆反力变化不大。因此，弹性地基梁对地基压缩模量不敏感，设计时不必过于纠结该参数的精确取值。

4 结论

针对地下水路堑段槽型挡土墙，进行不同荷载工况内力及变形分析，分析其计算模型的合理性，对墙背土压力作用状态、结构对地基承载能力的要求、墙外荷载的计算方法、抗浮措施及其安全系数取值、结构受力对地基压缩模量取值的敏感度等方面进行探讨，得出如下结论。

(1)边墙水平位移、转角位移较小，地下水位较高时边墙所受土压力大于主动土压力，因此墙背土压力宜按静止土压力计算。

(2)槽型挡土墙槽外活荷载为非主可变荷载，其对边墙的侧压力不宜与土压力采用相同的分项系数，建议参照德国铁路规范单独计算其侧压力，或采用弹性理论计算其侧压力。

(3)有条件时，优先采用底板外延方式抗浮。抗浮安全系数在考虑不小于1.0的结构重要性系数后取1.05。

(4)弹性地基梁对地基压缩模量不敏感，设计时不必过于纠结该参数的精确取值。