基于滑模控制的卡尔曼滤波在列车定位中的研究

葛 淼,张亚东,李科宏,邓祎宁

(西南交通大学交通信息工程及控制重点实验室,成都 611756)

1 概述

列车测速定位技术作为列控系统的三大关键技术之一，其准确度对于提高列车的安全性和运行效率有着重要作用[1-3]。在实际应用中，由于诸多因素的影响，测速定位误差不可避免。为了提高定位精度，专家学者提出了很多方法。文献[4]对列车位置进行了不确定性算法研究，该方法虽然保证了列车运行过程中的安全性，但由于对位置的估算都采用最恶劣情况，因此运行效率较低。文献[5]通过增加应答器数量，缩短应答器之间的间距来校准恶劣条件下列车的定位。虽然保证了整个定位的精确性，但是对整个系统而言，增加了造价成本和维修成本。文献[6]采用补偿方式，对空转打滑的位移误差进行修正。文献[7]采用改进联合卡尔曼滤波的算法，该算法通过其他信息采集器弥补了某些信息采集器可能出现的误差，适应能力强。文献[8]采用小波神经网络辅助卡尔曼滤波，其滤波结果和适应性都很好，但是其需要处理的数据量庞大。文献[9]采用了扩展卡尔曼滤波进行定位，该方法能够修正偏差较小的数据。

滑模变结构控制是变结构控制系统的一种控制策略。该控制可以使系统在一定特性下沿规定的状态轨迹小幅度、高频率的上下运动，即所谓的滑动模态。这种滑动模态可以通过调节相应的参数进行设计。由于滑模控制器的滑动模态与系统的参数及扰动无关，能够在一定程度上改善由空转或打滑引起误差，因此，采用基于滑模控制的卡尔曼滤波结构能够更加进一步的提高精度[10]。在参考上述文献的基础上，将基于滑模的改进卡尔曼滤波算法用于列车定位并通过仿真进行验证。

2 测速定位原理

本文采用最常见的脉冲速度传感器和加速度计组合定位的方式进行建模。

2.1 轮轴速度传感器工作原理

列车走行的距离主要是通过轮轴速度传感器得出[11]，其工作方式为：当传感器检测到车轮转动时即会产生一定的脉冲序列，那么根据脉冲序列可以计算出列车的走行距离[12]。

(1)

式中D——列车车轮直径，m；

nk——k周期的脉冲个数，个；

n——车轮转动1周输出的脉冲数；

yk——k周期列车里程计算值，m。

2.2 加速度计工作原理

加速度计是一种可以测量加速度力的电子设备。其工作原理是通过压电效应实现的[13]。加速度传感器内部晶体在加速度作用下形变而产生电压，电压又与加速度存在相应的关系。

电压值U与加速度a之间关系可表示为

U=φa

(2)

式中φ——压电系数。

3 卡尔曼滤波算法

3.1 轮轴速度传感器误差补偿模型

采用轮轴速度传感器能够减少数据处理和降低通信产生的负担，但在列车运行过程中，存在空转、打滑(这里暂不考虑测量误差)的误差，设dk为k周期列车运行时的补偿值；sk为k周期列车运行时，不含测量误差的真实值。因此，可以将式(1)改写为

sk=yk+dk

(3)

空转时，yk增加，则补偿值dk为负值；滑行时，sk减小，补偿值dk为正值。

3.2 加速度传感器误差补偿模型

在加速度测量过程中，由于机器本身测量过程中存在扰动，会产生一个误差，因此用εk来表示误差补偿，则

(4)

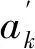
将上面两种误差设为过程误差。

3.3 状态模型的建立

首先离散化列车的走行过程，设采样时间为T，采样间隔足够小且为t。因为采样间隔足够小，可以将两个采样点之间看成匀加速运动，因此根据运动学公式可以得到

(5)

式中，ωk，μk分别为加速度和速度的合成误差，称为过程噪声。

3.4 观测模型的建立

对于列车定位来说，用轮轴速度传感器的里程计算值作为观测量能够简化程序。因此，这里将轮轴速度传感器的里程方程作为观测方程。

Sk=sk+Dk

(6)

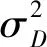
3.5 卡尔曼滤波模型求解

卡尔曼滤波模型的求解过程如下[14-16]。

将式(5)状态方程和式(6)观测方程用矩阵的形式表示成如下。

状态方程

X(k+1)=φX(k)+BA(k)+ΓW(k)

(7)

即

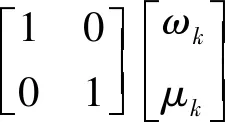
(8)

观测方程

Y(k)=HX(k)+V(k)

(9)

即

(10)

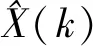
则：

(1)首先基于初始输入量预测下一个系统状态方程

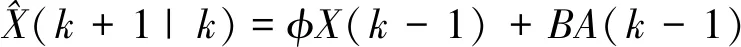
(11)

(2)此时的协方差为

P(k|k-1)=φP(k-1|k-1)φT+Q(k-1)

(12)

(3)滤波增益方程为

K(k)=P(k|k-1)HT[HP(k|k-1)HT+R(k)]-1

(13)

(4)根据前面的公式递推滤波估计方程

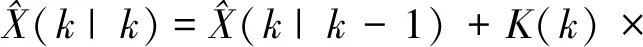
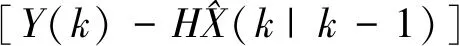
(14)

(5)相应的协方差更新

P(k|k)=[I-K(k)H]P(k|k-1)

(15)

4 基于滑模控制的改进卡尔曼滤波

对于组合定位来说，卡尔曼滤波求解的值在加减速过程中，空转和打滑造成的误差不能得到很好的修正。而滑模控制的滑动模态不受系统的参数和扰动的影响[17-18]，能够很好地降低由空转和打滑所带来的误差影响。因此采用基于滑模控制的改进卡尔曼滤波的方式来进一步减少空转和打滑所造成的误差。

则基于滑模控制的改进卡尔曼滤波结构如图1所示。

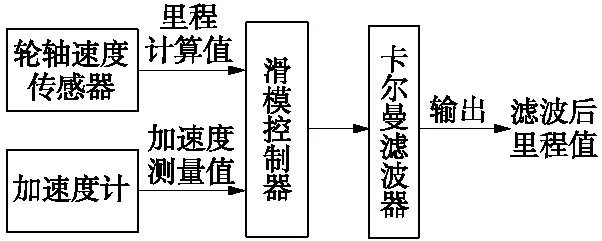
图1 基于滑模控制的卡尔曼滤波结构

由于这里主要讨论的是加速和减速过程中的空转和打滑的影响。假设加速度计只存在测量误差，不存在由于车体不平衡造成的过程误差。则滑模控制器的算法如下[19]。

(1)将轮轴速度传感器得到的里程计算值经滑模滤波后输出值设为yv，则

l(k+1)=y(k)+Cu(k)

(16)

式中，C为单位阵。

(2)确定位置指令r(k)，这里的位置指令即为真实值，即

r(k)=s(k)

(17)

(3)设位置指令的变化率为dr(k)，取

R=[r(k);dr(k)]，R1=[r(k+1);dr(k+1)]

(18)

(4)这里选取线性外推法预测r(k+1)及dr(k+1)，则

r(k+1)=2r(k)-r(k-1)

(19)

dr(k+1)=2dr(k)-dr(k-1)

(20)

(5)设切换函数为sqh(k)，则

sqh(k)=CeE=Ce(R-y(k))

(21)

式中，Ce=[c，1]。参数c表示滑模面的斜率。则切换函数的递推式为

sqh(k+1)=Ce(R1-y(k+1))

(22)

(6)设控制率为u(k)，结合式(7)，则

u(k)=(CeB)-1(CeR1-CeφX(k)-

CeBA(k)-sqh(k+1))

(23)

(7)设切换函数为指数趋近率，则

sqh(k+1)=sqh(k)+

t(-εsgn(sqh(k))-qsqh(k))

(24)

式中q——趋近速度参数；

ε——符号函数的增益参数；

sgn(x)——符号函数，其性质为，

当x>0，sgn(x)=1；

当x<0，sgn(x)=-1；

当x=0，sgn(x)=0。

(8)最后将得到的l值按照前面卡尔曼滤波的步骤进行求解。

同理可将加速度计得到的加速度值通过滑模得到相应的输出值。

5 仿真分析

由于获取现场数据较难，本文利用仿真数据对上面的算法进行分析说明。

设列车运行过程为一维运动；采样间隔t=0.01 s，根据文献[20]可知，对于卡尔曼滤波来说，系统噪声协方差矩阵Q设置越大，表示对状态方程置信度越低；观测噪声协方差R越大，表示对观测方程置信度越低；协方差矩阵P初值越大，表示对初值的置信度越低，算法收敛效果越好，但是P初值如果过大，算法结果会出现超调现象，震荡剧烈。因此，R、Q和P需要通过调试得出。

本文的仿真过程分为3个过程，即加速过程、匀速过程和减速过程。过程的真实值设定为：列车以-1 m/s2的加速度进行10 s的减速运动。

仿真中，在列车加速过程中加入空转误差随机数和测量误差随机数；在匀速过程中，只加入测量误差随机数；在减速过程，加入打滑误差随机数和测量误差随机数。即在整个仿真过程中不考虑由于车体不平衡造成的加速度计的过程误差。

首先采用卡尔曼滤波进行滤波，在卡尔曼滤波器参数设计中，观测噪声协方差R不宜过大，R越大，对观测结果越不置信，为了更好地反映滑模加卡尔曼合成滤波的效果，将参数设置为

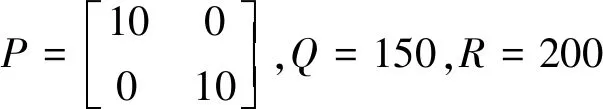
通过Matlab软件对加速过程进行仿真，得到的时间位移曲线如图2所示。

图2 卡尔曼滤波时间-位移曲线对比

从图2(a)可以看出，在加速阶段，卡尔曼滤波能够消除一定的抖动，但对加速过程中造成的空转误差修正结果较差。

从图2(b)可以看出，在匀速阶段，卡尔曼滤波能够一定程度上消除由测量引起的系统误差。

从图2(c)可以看出，在减速阶段，卡尔曼滤波能够消除一定的抖动，但对减速过程中造成的打滑误差修正结果较差。

然后采用基于滑模的改进卡尔曼滤波方式进行滤波。根据文献[21]可知，对于滑模控制来说，参数q主要影响切换函数的过程，参数c是滑模面的斜率，参数ε决定系统的抖振幅度。

为了直观地比较滤波结果，保持卡尔曼滤波器中的参数保持不变，通过仿真调节滑模控制器中的参数，则当滑模控制器中的参数如下时，结果较为理想。

通过Matlab软件得到时间-位移曲线，如图3所示。

图3 基于滑模的改进卡尔曼滤波时间-位移曲线对比

从图2和图3可以看出：

在加速阶段中，对于卡尔曼滤波来说，由于空转的影响使得其位移值远远大于真实值，其累计误差比真实值多出40.028%；而对于基于滑模的改进卡尔曼滤波值来说，其累计误差比真实值高4.324%。虽然还是存在一定的误差，但已经大大减小。

在列车匀速运行阶段，虽然卡尔曼滤波能够很好地降低系统误差，但基于滑模的改进卡尔曼滤波误差也要优于卡尔曼滤波的误差值。

在减速阶段与加速阶段类似，只是过程误差中的空转变成了打滑。

6 对比分析

目前，利用多传感器进行信息融合的方法是一种普遍采用的能够有效提高列车测速定位的方法。本文选取文献[7-9]的算法进行对比。

文献[7]采用了改进联合卡尔曼滤波，通过自适应算法，将测得的信息进行比例分配，对每个信息都要进行一次滤波，然后通过分配信息比例进行最后的滤波。该算法适应能力强，但对整个系统的结构要求很高。

文献[8]提出了采用小波神经网络辅助卡尔曼滤波，采用均方差作为研究变量，最终结果显示其均方差由改进前的0.15降低到改进后的0.01。虽然精确度很高，但是该结构复杂，数据庞大。

文献[9]采用了扩展卡尔曼滤波进行定位，首先通过扩展卡尔曼滤波对观测方程进行线性优化，结合盲区数据进行分析，从结论可以看出，在不发生大的偏移时，仿真结果较好。但并不适用于本文所述情况。

本文主要是针对轮轴传感器空转打滑产生的误差，这种情况属于较大的偏移量，采用基于滑模控制的卡尔曼滤波方法的矫正精度要优于采用扩展卡尔曼滤波的方法，更加具有适用性。从结构上来看，较之改进联合卡尔曼滤波和小波神经网络辅助卡尔曼滤波，基于滑模控制的卡尔曼滤波方法结构更为简单，易于理解与实现，在应用上能节约成本，同时定位精度也能得到一定的保证。

7 结语

主要针对目前轮轴测速传感器与加速度计组合定位下存在定位误差的问题进行分析。在卡尔曼滤波对空转打滑矫正效果不理想的情况下，利用滑模控制器的滑动模态与系统的参数及扰动无关的特点，提出基于滑模控制的卡尔曼滤波算法。该算法结构较之其他改进卡尔曼算法结构更为简单，通过仿真结果也可以看到：基于滑模控制的改进卡尔曼滤波方法能够在卡尔曼滤波算法的前提下进一步减小空转打滑误差，提高滤波结果的稳定性，同时也提高了列车定位精度。