支座刚度对高铁箱梁结构声辐射影响分析
罗 锟,欧开宽,雷晓燕,汪振国,张新亚
(华东交通大学 铁路环境振动与噪声教育部工程研究中心,南昌330013)
随着高铁桥梁占比的日益增多以及沿线居民环保意识的不断提高,其引起的环境振动与噪声问题也日益受到关注。当列车高速通过桥梁时,振动能量将通过轨道结构传递到桥面及其它构件,并激发其振动,振动能量将使桥梁各构件成为一个个声板,形成结构噪声的“声源”。振动严重时,振动能量通过桥梁墩台、土层和桩基传递给周边建筑,形成噪声的“二次辐射”[1–2]。桥梁结构噪声具有频率较低和衰减慢等特点,长期处于低频噪声环境中将对人们的身心健康造成极大的危害[3]。
目前,国内外学者对桥梁结构噪声进行了相关的理论和试验研究,并取得了一系列的研究成果。英国南安普顿大学声与振动研究所的研究比较具有代表性,其对铁路环境振动与噪声产生的机理、模型和控制方法进行了深入的研究[2];日本学者研究了公路桥梁低频噪声带来的危害,同时针对此制定了相应的法律规范[4];西南交通大学李小珍教授等采用边界元法对混凝土简支箱梁的结构噪声进行了理论分析,并且得到了外界因素对桥梁结构噪声的影响规律[5-6];同济大学李奇教授等基于车-线-桥耦合振动分析理论,通过边界元法求得模态声传递向量,研究了轨道交通混凝土U 梁的声辐射特性[7]。谢旭等结合车桥耦合振动理论和声传播理论,对交通荷载作用下桥梁低频噪声声场进行了实验分析和数值模拟,研究了地面的声反射作用对桥梁附近声场分布和声压水平的影响[8]。石广田等利用板壳单元,采用有限元-间接元法对高铁板式轨道箱梁结构噪声进行了研究[9]。夏禾等研究了桥梁阻尼、行车荷载等各参数对桥梁结构振动与噪声的影响程度[10]。
关于桥梁结构噪声研究较多,但支座刚度对桥梁结构声辐射的影响分析却相对较少。本文以京沪高铁32 m混凝土简支箱梁为研究对象,利用有限元和边界元的方法,对不同支座刚度条件下的箱梁结构声辐射特性进行研究。文中,有限元和边界元的方法利用1/10箱梁模型的有限元计算和试验验证。
1 声辐射的理论计算-边界元法
边界元法具有降维、误差小和适用于无穷域等优点,用来求解声学问题具有很大的优势。边界元法分为直接边界元法和间接边界元法,直接边界元的网格要求是封闭的,间接边界元的网格可以是封闭,也可以不封闭。因而直接边界元法可以计算封闭网格内部声场或是外部声场,但不能同时计算内外部声场,间接边界元法可同时用来计算内声场和外声场。为同时关注内声场辐射,本文采用间接边界元法。由于间接边界元计算网格在边界元网格两侧,因此,需要确定边界两侧速度差和声压差。将Helmholtz积分方程应用于边界表面两侧,通过计算其积分差值,可得声场中任意观测点的声压。结构在流体介质中振动,引发的声辐射问题要依次满足声波波动方程、流固界面的诺依曼(Neumann)边界条件以及萨摩菲尔德(Sommerfield)辐射条件,即式(1)、式(2)、式(3)。


式中:∇为拉普拉斯算子;p为声压;k=ω/c为波数,ω为圆频率;c 为声速;vn 为结构法向振动速度矢量;j为单位虚数;ρo为流体密度;r= ||Q-P,Q为结构表面S上的任一点,P为声场中的任意点;S为结构表面积。通过自由空间格林公式G(Q,P)=e-jkr/4πr,将Helmholtz积分方程应用于边界表面两侧,即可得声场中任意观测点的声压

式中:s(Q)、μ(Q)分别为Q 点表面两侧速度差和声压差,分别表示为
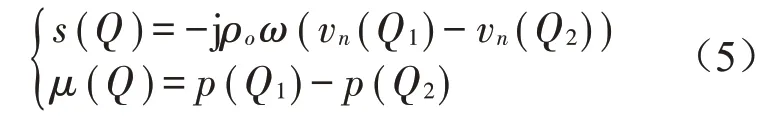
式中:p(Q1)、p(Q2)分别为结构表面Q 点两侧压力;vn(Q1)、vn(Q2)分别为结构表面Q点两侧法向振动速度。将结构表面用边界单元离散,则表面边界上各节点两侧速度差和声压差为

式中:C 为对称复数满秩矩阵,与结构表面形状、尺寸及插值形函数有关,并是激励频率的函数;f 为外激励向量,取决于结构表面振动速度。
对于结构表面外部任意观测点P,由式(4)得

式中:p(P)为任意观测点的声压;D为插值矩阵,由式(4)确定。
2 箱梁结构噪声计算方法
以京沪高铁32 m简支箱梁为研究对象,利用模型试验与有限元-边界元相结合的方法研究箱梁结构噪声问题,其步骤如下:
(1)按现有1/10 缩尺箱梁模型,建立箱梁有限元模型,并施加简谐荷载计算箱梁动响应;
(2)建立箱梁结构声学边界元模型,并提取箱梁结构振动响应导入Virtual.Lab软件中作为声学边界条件,计算箱梁结构声辐射。箱梁结构声学边界元模型建立时,最大单元的边长应小于计算频率最短波长的1/6,即单元边长应满足

式中:c为声音在介质中的传播速度,fmax为最高计算频率。
(3)利用模型试验的方法,实测不同场点的声压级,验证边界元模型与声学计算方法的正确性;
(4)利用以上被验证的模型和方法,重复步骤(1)和(2),采用京沪高铁箱梁原型的参数,计算不同工况条件下的箱梁结构噪声值。
建立高速列车-轨道耦合模型时,考虑轨道不平顺的影响,计算机车车辆行驶时轨道结构作用于箱梁结构上的动荷载。其中,轨道不平顺以德国轨道低干扰谱进行模拟,车辆为2 节CRH3 车辆编组,速度为200 km/h,详细的计算参数如表1所示;
京沪高铁简支箱梁有限元模型按照实际参数建立,其中梁体全长32 m,计算跨径为31.40 m,顶板宽12.00 m,底板宽5.5 m,梁高3 m;采用C50混凝土浇筑;桥上采用CRTS-II 型双线板式无砟轨道结构。利用有限元的方法建立箱梁有限元模型如图1所示。

图1 箱梁有限元模型
再将箱梁结构动荷载施加于箱梁有限元模型关键节点后,得到箱梁结构的振动响应。跨中断面典型位置的振动响应如图2所示。

图2 加速度振动响应
3 模型与方法的试验验证
以京沪高铁箱梁为原型制作1/10 缩尺模型,通过模型试验的方法验证箱梁结构声学计算模型和方法。
3.1 1/10缩尺箱梁振动试验
箱梁缩尺模型以京沪高铁箱梁为原型,按照几何相似比1/10 进行设计,采用自密实混凝土和钢丝等材料现场制作(成品如图3所示)。

图3 1/10箱梁缩尺模型
待养护28 天后测得梁体密度为2 203 kg/m3、弹性模量30×109Pa。模型箱梁和桥墩之间通过弹性支座连接,支座刚度为2.8×108N/m。
缩尺箱梁的振动试验过程为:首先,基于模型相似理论,理论推导缩尺箱梁与原型箱梁之间关键参数的相似关系,包括荷载、位移、速度和加速度响应等值的相似关系;然后,利用有限元方法建立原型箱梁与缩尺模型的有限元模型,分别进行模态分析和谐响应分析,验证原型与模型之间的相似关系;最后,利用模型试验的方法,获取1/10模型箱梁的自由模态和约束模态,验证模型箱梁与原型具有相似关系。
箱梁缩尺模型自由模态和约束模态的结果如表2所示。由表2结果可知,缩尺模型与原型具有相同的振动形态,且符合相似关系。缩尺模型的详细测试结果参见文献[11]。
3.2 1/10缩尺箱梁声学试验
试验目的:在半消声室内,实测1/10缩尺箱梁跨中断面声压级,验证箱梁结构噪声计算模型与方法。
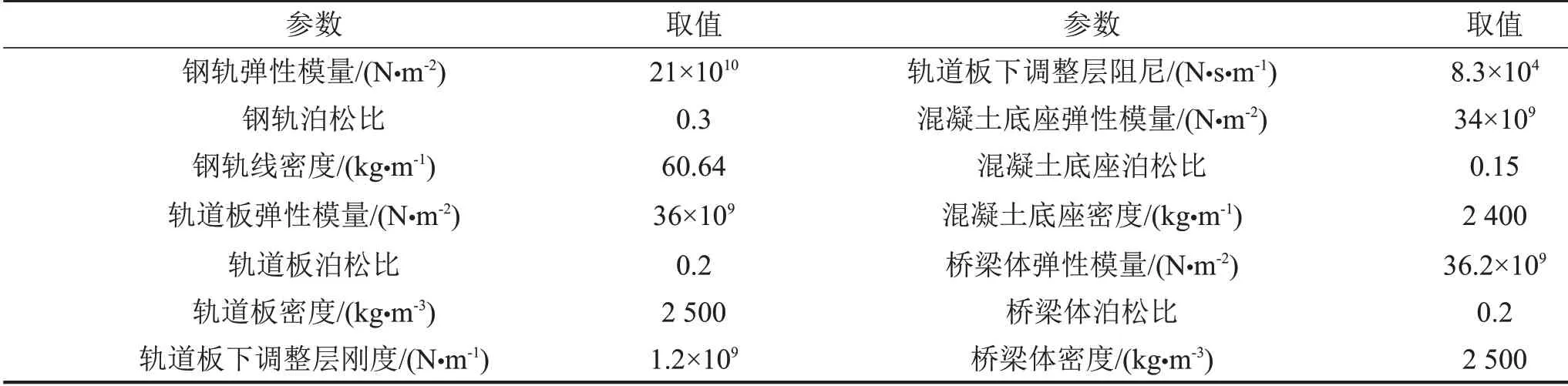
表1 高速列车-轨道耦合模型计算参数

表2 模态频率的理论与实测值对比/Hz
试验仪器:激振器、德国HEAD振动噪声采集分析系统和GRAS声学传感器。
传感器布置:在跨中断面布置6 个GRAS 声学传感器。包括,顶板上方0.03 m 和0.6 m 位置2 个,底板下方0.03 m 和0.6 m 2 个,翼板下方0.03 m 和0.5 m 位置2个,具体布置如图4所示。

图4 场点及激励点位置/m
激励:采用谐荷载在箱梁角点进行激励,荷载幅值为20 N、频率为1 Hz~200 Hz,方向向上。测试前,对激振器做一定的隔声处理,尽最大可能避免影响测试结果。
测试共分3组进行,每组测试时间为60 s。实测图如图5所示。

图5 声压级实测图
3.3 缩尺箱梁声学计算与分析
模型试验的同时,利用有限元和边界元相结合的方法,按照步骤(1)和(2)计算箱梁跨中断面不同位置的声压值。计算频率同测试频率,为1 Hz~200 Hz。同时考虑到地面反射作用,用障板模拟地面。为便于验证,在数值计算时,提取同测试场点相同位置的计算结果进行对比,结果如表3所示。

表3 实测声压级与仿真值对比/dB
通过对6个场点的实测结果和数值计算结果对比分析,可知实测结果和预测结果较为相近,多数场点仅相差1 dB,只有场点6 一点相差3 dB。因此可以认为本文所建立的箱梁声学仿真计算模型与方法是正确的,用该模型来计算箱梁的结构噪声结果是可靠的。
4 支座刚度对简支箱梁结构声辐射影响分析
为了对比分析不同支座刚度对简支箱梁结构声辐射的影响,选用3种不同型号支座进行分析计算,其刚度分别是:A 型支座:3.38×109N/m;B 型支座:1.13×108N/m;C 型支座:2.33×107N/m;将上述不同刚度值工况下有限元中箱梁结构部分振动响应结果作为边界条件,通过声学软件Virtual.Lab 边界元中内置模块离散FFT 进行时频转换,然后进行结构声辐射求解。
由模态分析可知,箱梁前20阶的模态频率均低于100 Hz,且考虑到计算时长与效率问题,因此本文仅分析1 Hz~100 Hz 内结构噪声。分析时,在箱梁跨中断面建立一个24 m(垂向)×56 m(横向)的面声场及4个场点,具体为:箱梁中心线下距底板垂向距离为2 m和10 m的N1和N2;距底板10 m、横向距离依次9 m和18 m的N3和N4,详细位置如图6所示。
4.1 声功率分析

图6 跨中断面场点示意图
声功率反映的是声源在单位时间内辐射的能量指标。利用上述模型,可得到不同刚度支座条件下梁体声功率辐射曲线,结果如图7所示。

图7 声功率辐射曲线图
由图7可知,
(1)在1 Hz~48 Hz 范围内,支座刚度越大,声功率辐射值越小,但3 种工况条件下的声功率曲线变化趋势较为相近,支座刚度对声辐射的影响较小;
(2)在48 Hz~100 Hz 范围内,声功率曲线基本重合,支座刚度对声功率几乎不产生影响;
(3)支座刚度越大,声功率峰值越小。由图可知,三种不同工况条件下的声功率峰值,分别出现在19 Hz、3 Hz 和3 Hz,对应的声功率分别为115 dB、118 dB和120 dB。
4.2 声压级分析
箱梁结构噪声多以低频为主,因此采用线性计权声压级进行分析。不同刚度支座条件下的线性声压级如图8所示。
由图8可知:
(1)在1 Hz~20 Hz范围内,各场点声压级变化与声功率变化趋势较为接近;
(2)三种支座在相同场点的声压级变化趋势较为接近,但支座刚度越大,声压级越小;
(3)在同一场点,支座刚度越大,声压级峰值越小;
(4)声压级随距离的增加而减小。如A型支座条件下4个场点最大声压级分别为92 dB、86 dB、81 dB和73 dB;B型支座条件下4个场点最大声压级分别为99 dB、91 dB、87 dB和81 dB;C型支座条件下4个场点的最大声压级分别为100 dB、93 dB、90 dB和84 dB;
(5)不同支座条件下箱梁结构噪声最大声压级均出现在较低频段,分别为19 Hz(A 型支座)、3 Hz(B型支座)和3 Hz(C型支座)。
4.3 跨中场点二维声场分析
不同工况条件下的声压级峰值多集中于1 Hz至20 Hz范围内,图9为跨中断面峰值频率下的二维声压级分布云图。从声压级分布云图可知:
(1)箱梁结构噪声辐射峰值多集中于梁体正上方和正下方,且呈上下对称分布;
(2)箱梁结构噪声具有明显的指向性,在顶板和底板处声压级较大,斜上方和斜下方声压级较小;
(3)支座刚度值越大,最大声压级越小。其中,A型支座的最大声压级为95 dB,B型支座的最大声压级为105 dB,而C型支座的最大声压级为107 dB。
5 结语
本文以京沪高速铁路32 m 简支箱梁为研究对象,运用模型试验与有限元、边界元相结合的方法,研究了不同刚度支座条件下的箱梁结构噪声辐射特性,得到以下主要结论:
(1)采用模型试验的方法进行箱梁结构噪声的研究,得到的结果是可靠的。
(2)在1 Hz~48 Hz 范围内,支座刚度越大,箱梁声功率辐射值及峰值越小。
(3)箱梁最大声压级主要集中在1 Hz~20 Hz;3种支座在相同场点的声压级变化趋势较为接近,但支座刚度越大,声压级越小;
在同一场点,支座刚度越大,声压级峰值越小。
(4)在48 Hz~100 Hz内,支座刚度值对梁体的声功率辐射及场点声压级大小影响不大。
(5)不同支座条件下箱梁结构噪声最大声压级均出现在较低频段,这为桥梁减振降噪提供了一种思路:针对支座刚度值较小的桥梁可优先考虑消除频率较低处的噪声。

图8 跨中断面场点线性声压级

图9 跨中断面场点二维声场云图/dB
(6)在1 Hz~20 Hz范围内,各不同刚度值支座所产生的结构噪声具有明显的指向性。

