《实际问题与一元一次不等式》教学设计
◎韩玲
一、教学目标
知识目标:能利用一元一次不等式解决“哪家商场购物花费少”这类含有不等关系的方案选择类实际问题.
技能目标:通过观察、思考、讨论等活动,积累利用一元一次不等式解决实际问题的经验,提高分类讨论问题的能力.
情感目标:在积极参与数学学习活动的过程中,感受生活处处有数学,逐渐养成从数学的角度思考问题的习惯.
二、教学的重点
分析方案选择类实际问题中的不等关系,列出一元一次不等式;
三、教学难点
如何从方案选择类实际问题中抽象出不等关系,建立不等式模型进行求解.
四、教学过程的设计
1.问题引入
老师昨天和朋友去百富考霸吃饭,点了一个大漠烤鸡(49元),两个汉堡(36元),一份薯条(8元),两杯奶茶(16元).服务员建议我购买套餐(套餐:两个汉堡,两杯热饮,一份薯条,一个大漠烤鸡,共计99元).
问题1:你们认为老师是否应该购买套餐?
师生活动:学生自由发表意见
设计意图:贴近生活的问题情境可以把学生拉入到一个亲切、轻松的环境中,让学生主动思考.
问题2:你能用一个数量关系,表示你的建议的合理性吗?
师生活动:引导学生发现,选择问题中的不等关系,能借助不等式进行表述.
设计意图:让学生感受,买不买套餐,关键是看哪一种花费更少.花费更少体现的是不等关系,可以用不等式来表示.从而引出本节课课题,一元一次不等式的应用.
2.新课探究
甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费.顾客在哪家商场购物花费少?
问题1:如果要买一个30元的耳机,选哪家商场花费少?如果要买80元的书包呢?200元的钢笔呢?
师生活动:学生回答,教师指导学生准确计算、比较、得出结论.
设计意图:引导学生感受,由于优惠起点的不同,需要分类讨论,问题生活化,具体化,让学生比较容易列出每种情况对应的算式.
问题2:如果购物款累计达到x元,你能用含x的式子分别表示顾客在两家商场花费的钱数吗?
师生活动:学生回答,其他同学补充,教师引导完善,并用表格表示在黑板上.
设购物款累计达到x元.

购物款 在甲商场花费 在乙商场花费0<x≤50 x x 50<x≤100 x 50+0.95(x-50)x>100 100+0.9(x-100) 50+0.95(x-50)
设计意图:通过列式子,让学生将在问题1中感受到的,需要分类讨论的消费情况表示出来.
问题3:你能从表格中直接看出,哪家商场花费少吗?
师生活动:学生思考,交流.师生共同分析讨论,发现
(1)如果累计购物不超过50元,则在两家商场购物花费一样;
(2)如果累计购物超过50元,但不超过100元,则在乙商场购物花费少;
(3)如果累计购物超过100元,不能确定到哪家商场购物花费少,需要再进行分类讨论.
设计意图:借助表格,学生直观地看出,当累计购物不超过100元时,可以确定到哪家购物花费少,但是当累计购物超过100元时,不能确定,需要继续分类讨论.
问题4:如果累计购物超过100元,在两家商场花费会出现哪些情况?
师生活动:引导学生得出结论,可能会出现三种情况:甲商场花费少;乙商场花费少;两商场花费一样.根据上述分析,引导学生发现三种情况中的不等关系,学生分小组讨论,教师指导,学生小组汇报.
当x>100时,
若在甲商场购物花费少,则100+0.9(x-100)<50+0.95(x-50)
解得 x>150
若在乙商场购物花费少,则100+0.9(x-100)>50+0.95(x-50)
解得 x<150
若在两个商场购物花费一样,则100+0.9(x-100)=50+0.95(x-50)
解得 x=150
即当累计购物超过150元时,在甲商场购物花费少,累计购物超过100元但不超过150元时,在乙商场花费少,累计购物150元时,在两家商场花费一样.
设计意图:学生经历从实际问题中找出数量之间的不等关系,并用不等式来解决问题,体会建立不等式模型解决实际问题的过程.
问题5:你能借助数轴,把选择商场的情况表示在数轴上吗?
师生活动:学生尝试,教师指导,完善.
学生在黑板上展示:
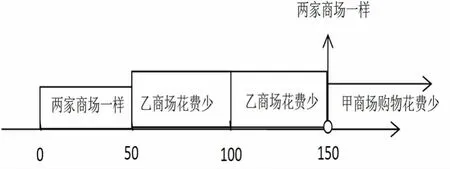
设计意图:学生借助数轴将分散的讨论进行综合,体会数形结合的思想.教师引导学生及时归纳、总结,培养学生有条理地思考和表达的习惯.
问题6:借助数轴,综合上面的分析,你能给出一个合理的选择方案吗?
师生活动:学生得出:购物不超过50元和刚好150元时,在两家商场购物,花费一样;超过50元但不到150元时,在乙商场购物花费少;超过150元后,在甲商场购物花费少.
设计意图:学生能够将数学问题的解转化为实际问题的解.
3.归纳总结
请同学们思考并回答:
(1)生活中,在选择哪家商场购物时,如果需要分类讨论,一般会有几种情况?
(2)我们在购物时面临的选择问题可以利用不等式来解决,利用不等式解决实际问题的步骤是什么?
设计意图:通过总结本节课所学,让他们感受身边中的不等关系,感受数学来源于生活,生活中更需要数学.
4.布置作业
教科书习题9.2第5、6题
补充题:下表给出的是两种移动电话的计费方式:

月使用费/元 主叫限定时间/min 主叫超时费/(元/min)被叫方式一 58 150 0.25免费方式二 88 350 0.19免费
你觉得选哪种业务更优惠?
设计意图:补充题是七上一元一次方程的例题,改编问题后可以用不等式来解决.一方面,学生对问题背景既有生活经验,也有学习基础,另一方面,通过此题,让学生再次巩固上课所学购物选择类问题,加深印象.
五.教学反思
本节课从学生身边的实际问题出发,从学生已有的认知出发,激发学生的学习兴趣,调动他们的积极性.引入问题贴近学生,数据明确,学生容易解决,为后面用不等式解决选择类问题做了铺垫,使新课内容更容易理解.通过用含有x的式子表示实际花费,使学生加深对数学建模中的“符号化”的理解与运用.借助表格,让学生直观地对比,对累计购物不超过50元和超过50元但不超过100元的情况得出结论.利用数轴,直观地综合所有分类,培养学生数形结合的思想.教师在教学中关注学生对待学习的态度是否积极,关注学生参与度和思考层次能否在引导下得到进一步的提升,关注学生能否把实际问题中的不等关系,抽象成不等式,并利用不等式解决实际问题,关注学生能否从数学的角度考虑问题.

