系杆拱桥吊杆索力计算方法对比分析研究

许汉铮, 蔡昌伟, 李浩师

(长安大学 公路学院，陕西 西安 710064)

0 引 言

钢箱系杆拱桥造型优美，结构轻巧，跨越能力大，但结构受力复杂[1]，一般采用分阶段逐步完成的施工方法，其吊杆索力和桥梁结构内力、变形也随施工阶段不断发生变化[2-3]。采用临时支架施工的下承式钢箱系杆拱，为保证拆除拱肋支架时全桥的受力和线形，须进行吊杆初张拉；拆除下部支架的支撑点时，须进行吊杆二次张拉。为减少调索工作量，须确定合理的二次施工索力以保证最终成桥状态与合理成桥状态[4]相近。目前确定系杆拱桥合理施工状态的索力问题与斜拉桥的施工索力问题具有相似的研究方法，如正装倒拆优化法[5]、无应力状态法[6]、差值迭代法[7-8]、正装迭代法[9-10]等。但鉴于调索方法众多，设计施工人员并不能快速准确的确定一种适用于系杆拱桥合理施工调索的方法。鉴于此，笔者基于差值迭代法、正装迭代法应用于同一系杆拱桥进行有限元分析，对比分析合理施工状态及成桥状态下的结构受力，研究两种方法的适用性，得出何种计算方法更适用于确定系杆拱桥的合理施工索力。

1 合理施工索力计算原理

1.1 差值迭代法

设索力控制参数为n，以合理成桥状态下的吊杆索力为目标索力，记为:

{F}=(f1,f2,…,f3)T

(1)

按照实际施工顺序张拉吊杆，每次张拉一组吊杆作为一个施工阶段。拟定初吊杆索力，记为：

{T0}=(t1,t2,…,tn)T

(2)

将{T0}输入到有限元软件中计算，得到初吊杆索力对应的成桥索力，记为：

(3)

此时，目标索力与成桥索力与存在一个差值：

{T0}={F}-{F0}

(4)

为减小差值，由式(4)再确定一组张拉索力：

{T1}={T0}+{ΔT0}

(5)

式(5)所得索力再次输入有限元软件中，计算对应的成桥索力{F1}。如此循环，最终得到成桥索力与目标索力的差值：

{ΔTi}={F}-{Fi},i=0,1,2

(6)

当满足：

(7)

即成桥索力{Fi}收敛。一般工程中可取：ξ1≤0.5%,ξ2≤5%。

1.2 正装迭代法

与差值迭代法类似，拟定一组吊杆索力{T0}，按实际吊杆张拉顺序得到索力影响矩阵[A1]n×n和相应成桥索力{F0}。单位力张拉第i号吊索时，计算出j吊杆的影响系数aij，最终组成一个矩阵即为索力影响矩阵：

(8)

将目标索力与成桥索力作差值，即：

{b}={F}-{F0}

(9)

记吊杆索力的调整量为:

{X}=(x1,x2,…,xn)T

(10)

式(10)与式(8)、式(9)构成矩阵方程组 ：

[A1]{X}={b}

(11)

利用数学软件MATLAB可求解：

{X}=[A1]-1{b}

(12)

然后进行吊杆索力修正，即：

{T1}={T0}+{X}

(13)

式(13)所得索力再次输入有限元软件中进行正装计算，生成新的影响矩阵[A2]n×n和成桥吊杆索力{F1}。重复上述迭代过程，直到{Fi}能收敛到目标索力{F}。收敛准则和差值迭代法一致，见式(7)。

2 工程概况

研究对象为一单孔123 m下承式钢箱系杆拱桥，桥宽15.3 m，纵、横桥向对称，结构总体布置如图1。除桥面板为钢混组合结构外，其余全为钢结构。拱圈计算跨径L=120 m，失高为24.16 m，矢跨比为1/5，拱轴线为二次抛物线。拱圈为两个分离式的矩形钢箱，中心间距为13.7 m，拱肋高为2 m，宽为1.6 m，拱肋截面顶、底板、腹板均各设置两道加劲肋，拱肋间全桥设置3道风撑。纵向系杆为矩形钢箱，系杆之间对应吊杆的位置设有矩形钢箱横梁。

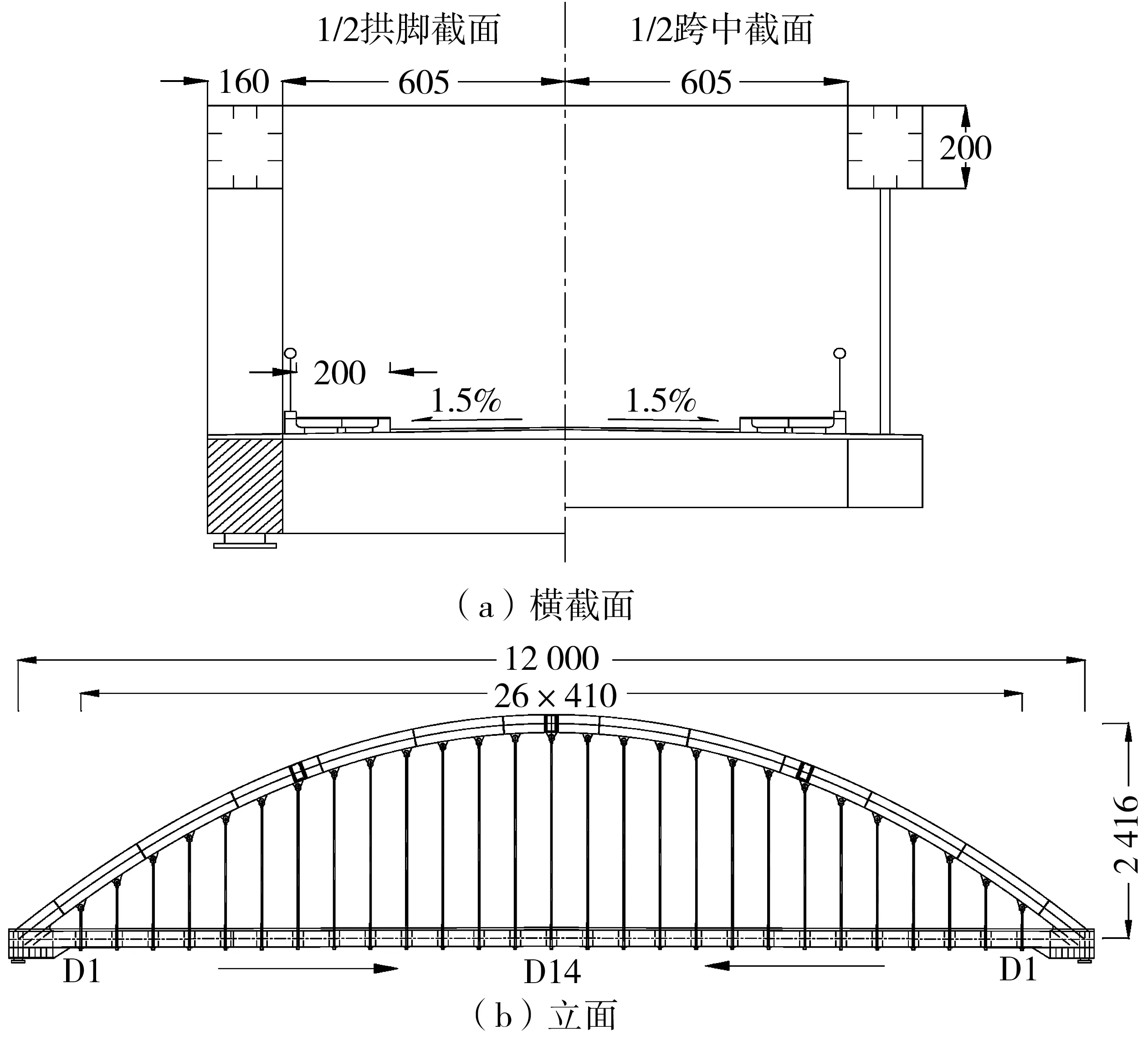
图1 系杆拱桥总体布置(单位:cm)Fig. 1 General layout of the tied arch bridge

吊杆采用PES.E(FD)7-37环氧喷涂拉索，强度等级为1 670 MPa，吊杆间距为4.1 m，单侧共27对吊杆。吊杆下端采用OVMAM7-37(IV型)冷铸锚具，上端为插销式吊耳。桥梁结构各种材料属性如表1。

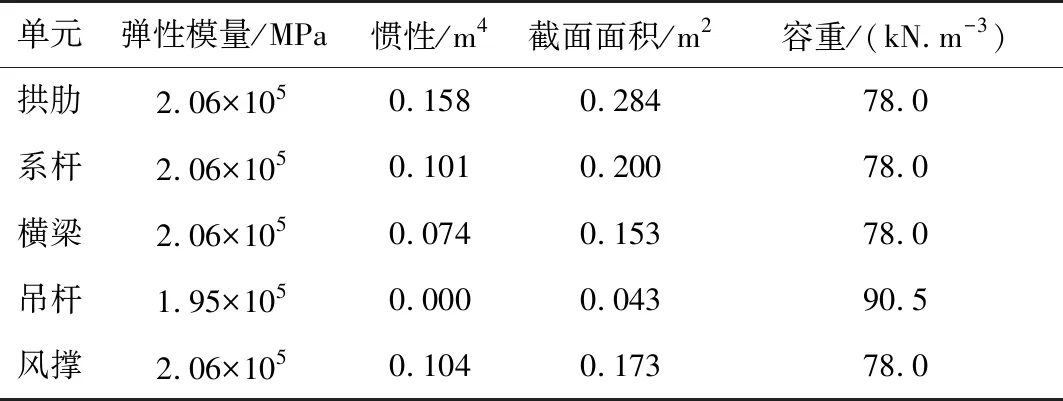
表1 材料属性 Table 1 Material property

系杆拱桥采用先梁后拱的施工方法。拆除拱肋支架时安装所有吊杆，从拱脚向拱肋跨中进行初张拉，每次对称张拉4根吊杆，索力值均为100 kN。待拆除系梁支架时，对吊杆进行二次张拉。采用有限元方法对全桥进行建模，精确模拟各个施工阶段。算例采用影响矩阵法[11]求得目标索力值，见表2。

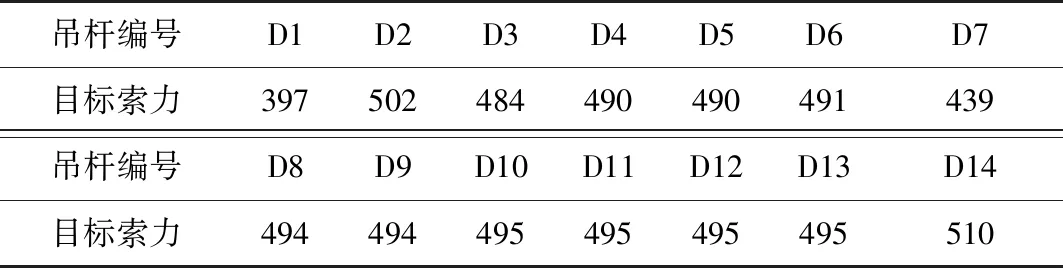
表2 目标索力值以及各参数 Table 2 Values of target cable force and various parameters kN

3 迭代计算结果

3.1 差值迭代法计算结果

为使差值迭代法加速收敛于目标索力，选择目标索力与初张拉索力差值作为初始迭代索力。每次迭代后吊杆成桥索力值{Fi}见表3。

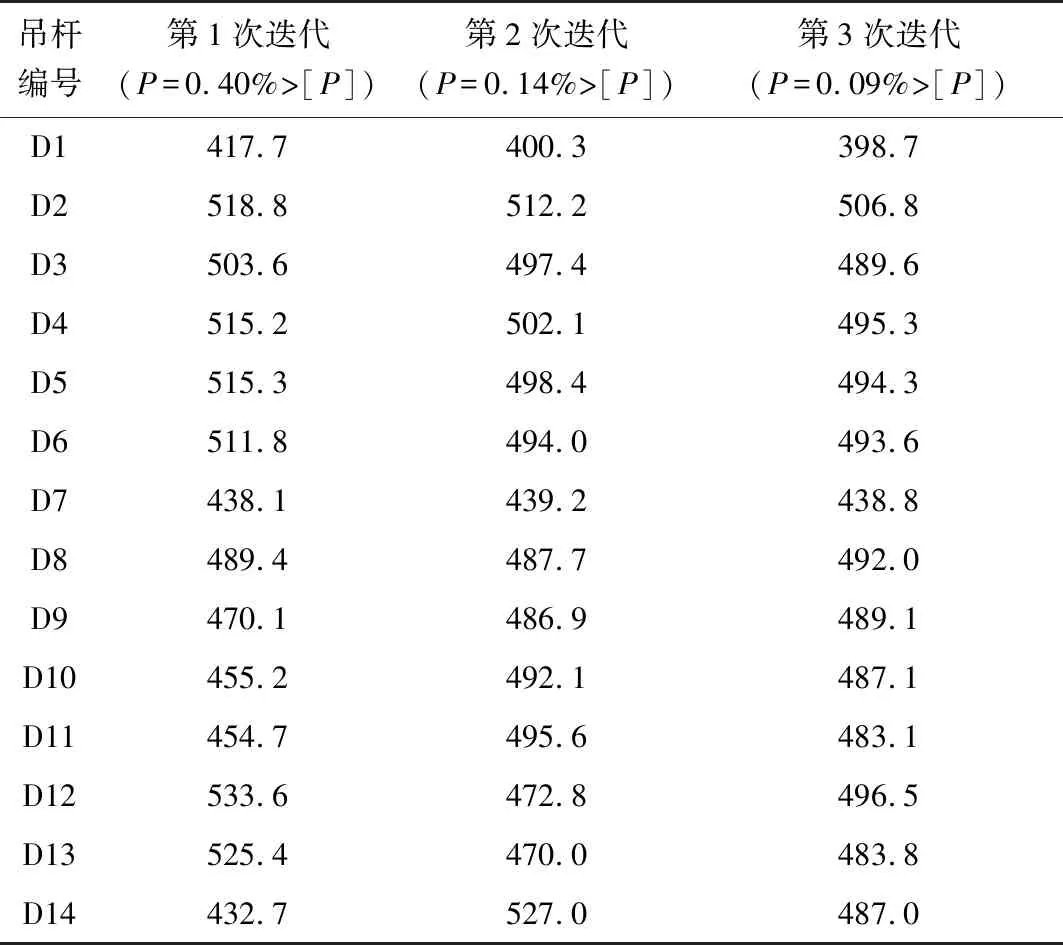
表3 吊杆成桥索力差值迭代法计算值 Table 3 Calculated value of suspender bridge cable force by difference iteration method kN

表3列出了差值迭代法计算的吊杆成桥索力值，3次迭代后，成桥索力与目标索力最大相差4.51%，控制在误差范围内。经计算：当进行第4次迭代后，吊杆索力最大误差比减小2.4%，计算精度显著提高；当短吊杆满足精度要求时，可直接对长吊杆进行迭代计算，收敛速度也明显加快，且同样获得较高计算精度。

3.2 正装迭代法计算结果

取目标索力与初张拉索力差值作为初始迭代索力。在形成影响矩阵时，取小数点后3位有效数字以减小后期计算带来的误差。初次影响矩阵如式(14)。

由式(10)可以明显看出:当张拉某组吊杆时,相邻吊杆索力值均减小,且长吊杆影响较短吊杆大,但离张拉吊杆较远处时,吊杆表现为索力值增大。

每次迭代后吊杆成桥索力值{Fi}见表4。

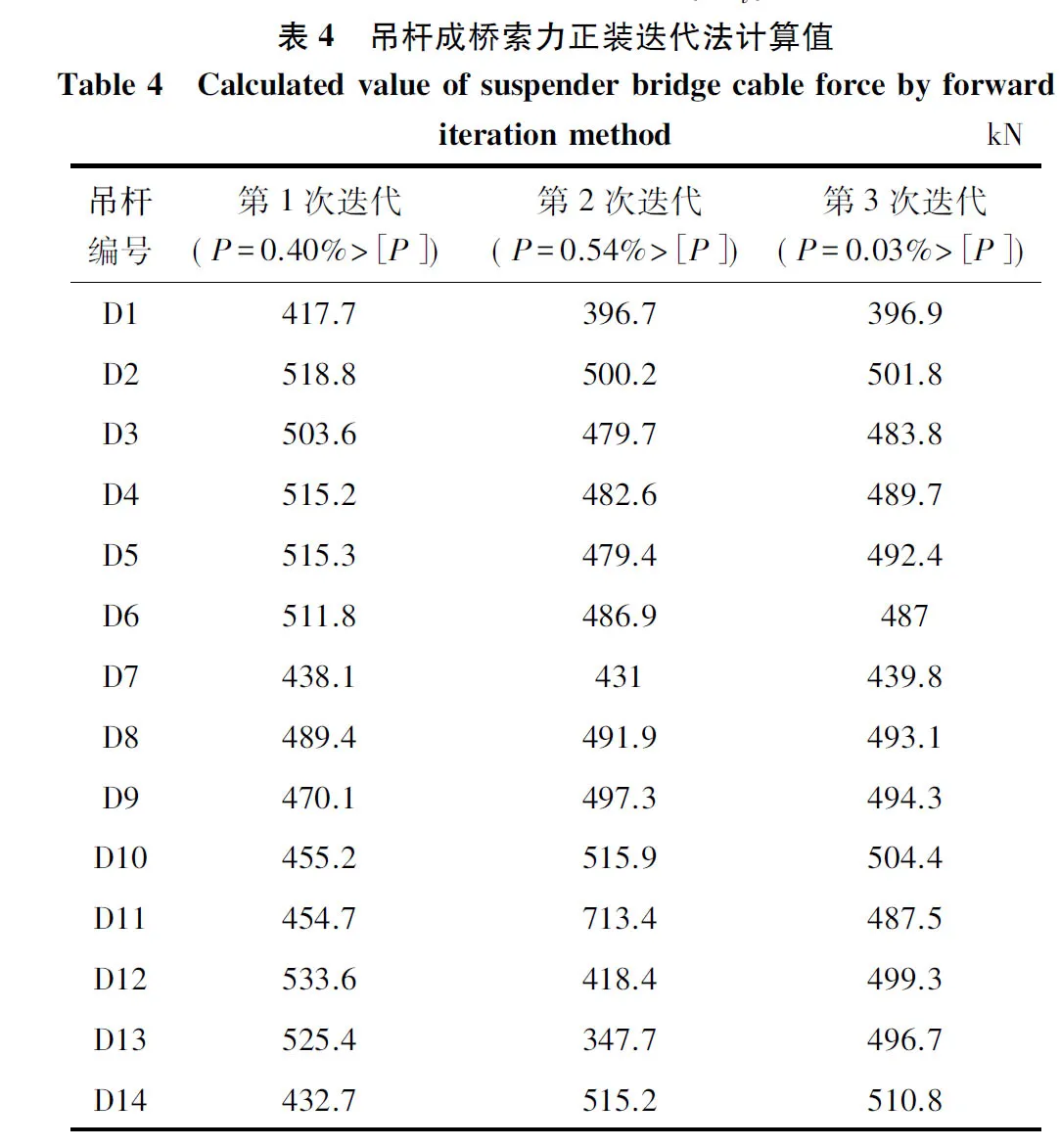
表4计算结果表明:利用影响矩阵求解的正装迭代法与差值迭代法相同,3次迭代即能满足计算精度要求。但3次迭代计算下,吊杆索力值的最大误差仅为1.9%,比差值迭代法精度高2.61%。

4 施工索力、成桥索力及拱桥内力、线型对比分析

4.1 施工索力对比分析

通过以上两种迭代法计算,吊杆施工索力均快速收敛于目标索力,但施工索力值差异性大,其各次迭代索力值对比如图2。

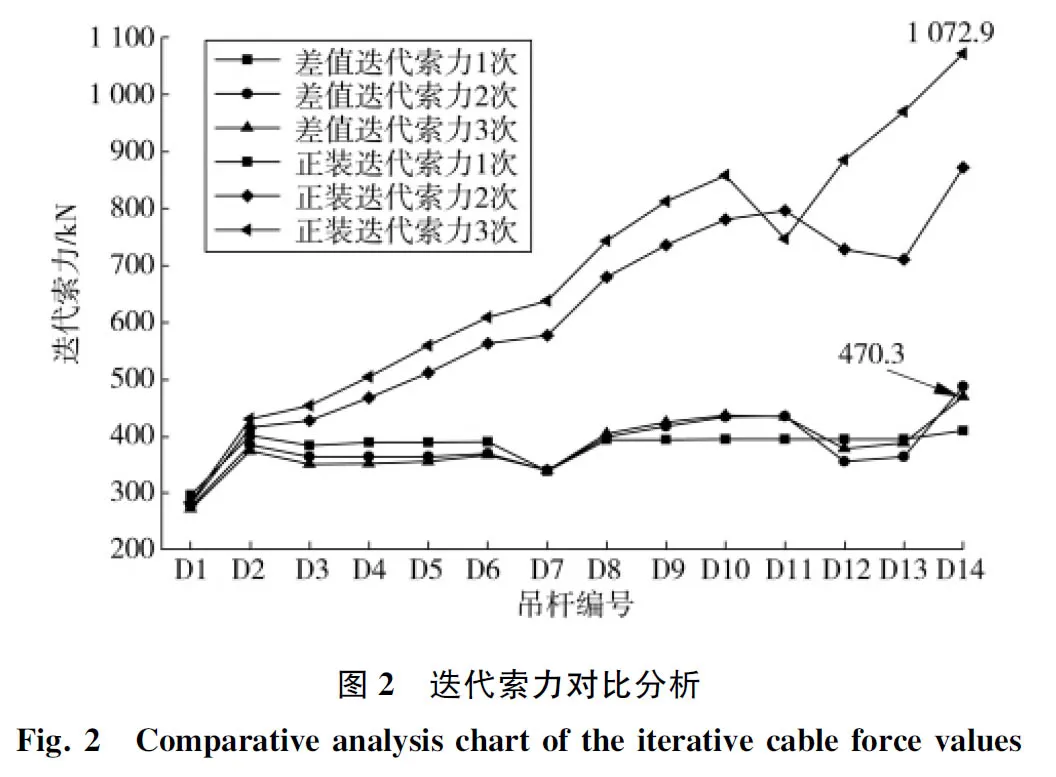
由图2可知:差值迭代法的施工索力较正装迭代法均匀,有利于单根吊杆受力,便于施工;正装迭代法的施工索力为从拱脚到拱顶大致呈线性递增趋势,最大张拉索力的吊杆为D14,应力753 MPa<0.5fpk=835 MPa,安全系数低,但满足施工阶段吊杆索力安全要求。

4.2 成桥索力对比分析

两种方法在迭代过程中,目标索力与成桥索力误差比变化曲线如图3。可以看出:两种方法中短吊杆的索力收敛速度均明显快于长吊杆;差值迭代法的误差整体波动较正装迭代法大,且随着迭代次数增加,后者收敛速度明显快于前者,最后一次迭代 后者误差几乎趋近于零,收敛精度明显高于前者,但从迭代计算时间分析比较,前者却明显优于后者。

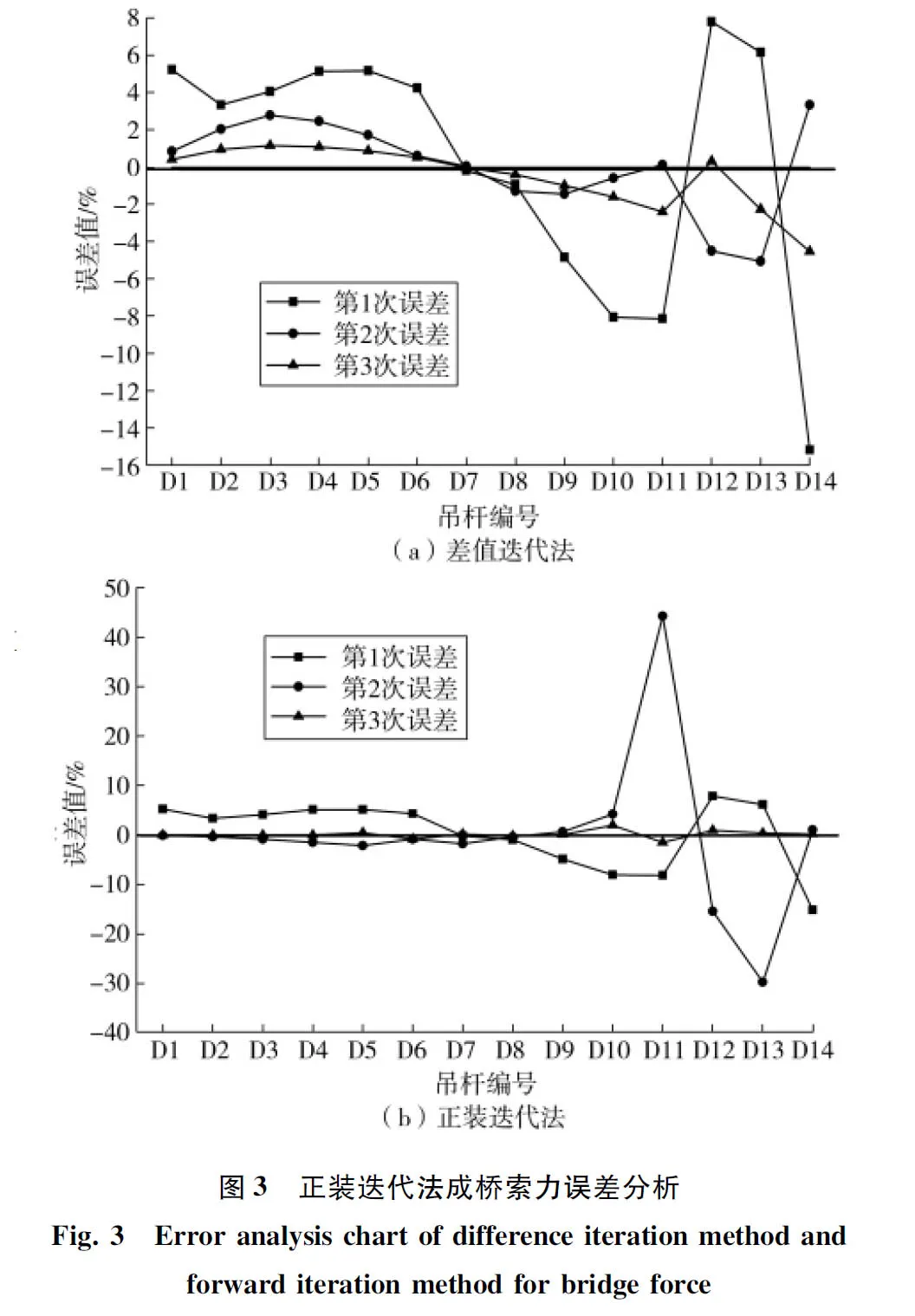
4.3 结构内力、线型对比分析

索力调整时,各施工阶段及成桥状态下关心截面的变形和应力为主要控制内容。经施工阶段受力分析,在各施工阶段结构变形和应力均满足规范要求。

在两种迭代法各次迭代计算后,成桥状态下系杆、拱肋关心截面变形及应力如图4、图5。通过图4(a)对比分析可以明显看出:正装迭代法计算下的系杆竖向变形变化规律与差值迭代法有显著差异,前者系杆竖向变形与合理成桥状态最大误差仅为12.32 mm,系杆整体变形较后者均匀,但后者竖向变形曲线为二次抛物线,且未超过规范容许值,有利于提供良好的施工预拱度线形,便于施工。

对比分析图4(b)中的拱肋竖向变形曲线可以看出:两种迭代法随着迭代次数累积,对其拱肋的竖向变形并无较大影响;迭代方法的不同并不影响拱肋的竖向变形,拱肋竖向变形均达到60 mm左右,可通过设置施工预拱度来消除此变形,使拱肋线形符合设计要求。

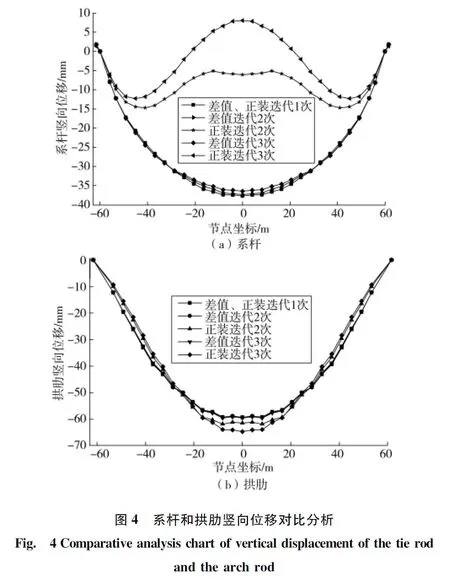
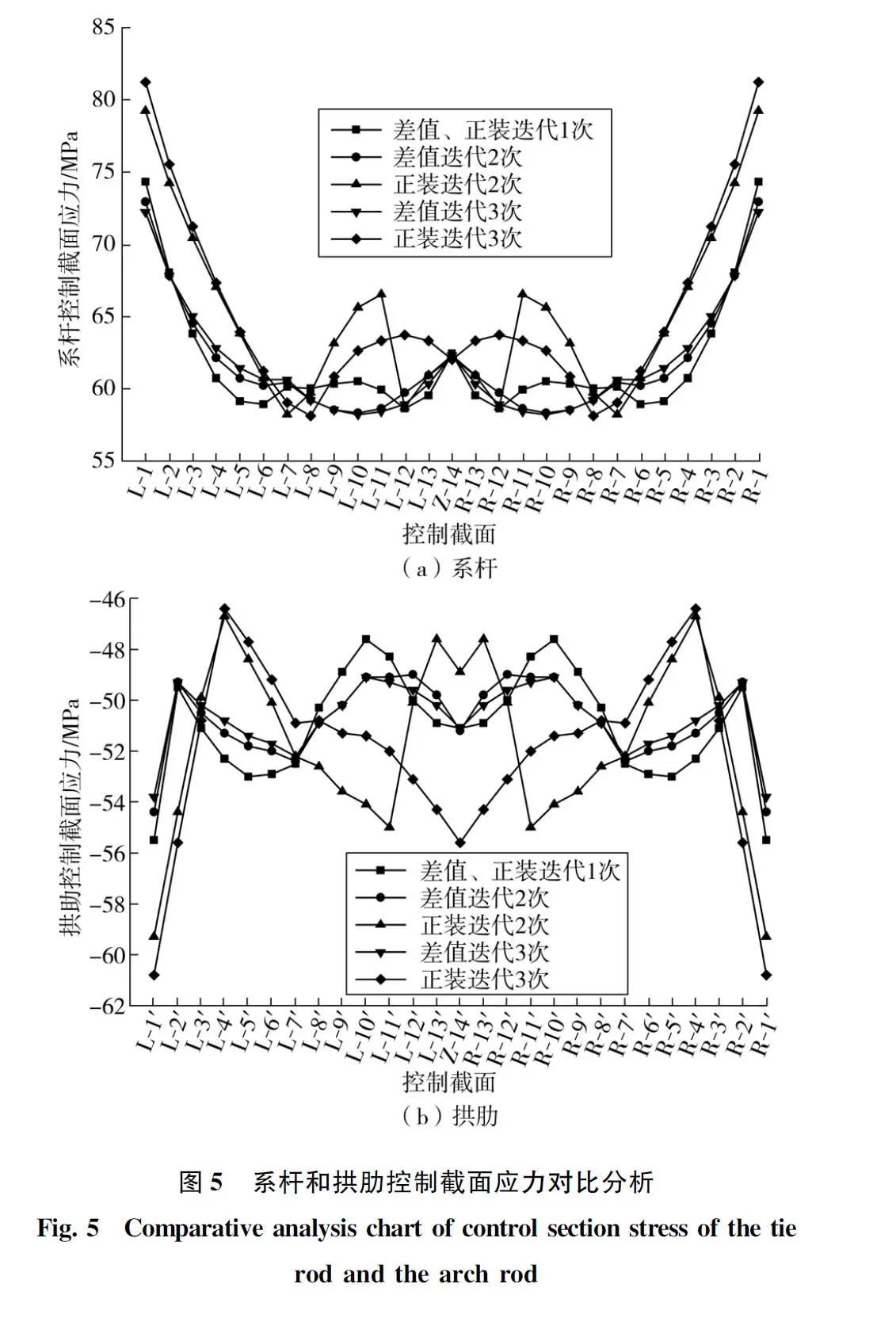
图5为系杆和拱肋控制截面应力对比分析结果。图5 中“-”为压应力,“+”为拉应力。系杆与横梁连接处为控制截面,截面编号与拱桥纵断面前进方向一致。拱肋与吊杆连接处为控制截面,截面编号与拱桥纵断面前进方向一致。

图5中对比分析结果表明:两种迭代法所得系杆、拱肋应力沿跨径分布不均匀,但在各次迭代成桥状态下,系杆1/2关心截面处应力相等。

二次施工索力张拉完成后,系杆和拱肋最大应力分别为81.2 MPa(拉应力)和60.8 MPa(压应力),均发生在拱脚处,两者均远小于Q345钢材的容许容许应力,符合设计安全要求。差值迭代法在各次迭代计算所得的系杆和拱肋控制截面应力中变化规律相似,所得系杆及拱肋应力整体低于正装迭代法,有利于系杆拱的受力。正装迭代法在系杆及拱肋的1/4～1/2处应力波动较大。

5 结 论

1)提出的差值迭代法和正装迭代法确定系杆拱桥二次施工索力,计算结果均符合相关规范要求,具有较好的实用性。

2)差值迭代法原理简单,避免计算繁琐的影响矩阵,简单快捷,所得二次施工索力均匀,系杆形变曲线线形、系杆应力及拱肋应力均优于正装迭代法,有利于系杆拱的受力。

3)正装迭代法用较少迭代次数获得较高迭代精度,较差值迭代法收敛快,但计算繁杂。二次施工索力与差值法相比呈线性递增趋势。跨中吊杆索力应力达到极值753 MPa安全系数低,不利于施工控制。

4)通过两种迭代方法在实际工程的应用对比分析,可以得出差值迭代法计算方便快捷,迭代索力更有利于整体结构受力,便于设计施工人员使用。至此,笔者在确定下承式钢箱系杆拱的二次施工索力时优先采用差值迭代法。