DSMC量子动理学化学反应模型的数值模拟

李锦，耿湘人，陈坚强，江定武，李红喆

1. 中国空气动力研究与发展中心 计算空气动力研究所，绵阳 621000 2. 中国空气动力研究与发展中心 设备设计及测试技术研究所，绵阳 621000

高超声速飞行器，经常在稀薄气体环境中飞行，面临极端速度和高度[1]。当钝头体高超声速飞行器以近乎轨道速度再入大气层时，其头部激波之后将出现超过20 000 K的高温。这样的流动条件会激发分子的振动模态，并导致离解反应的发生。置换反应和原子的复合反应将在冷的催化壁面附近以及气体绕过飞行器肩部的膨胀流动中发生[2]。高超声速稀薄流动中的化学反应过程将显著改变飞行器周围流场的特征，影响飞行器表面的温度、压力和热流以及飞行器的气动性能[2]。如果不考虑化学反应，就无法精确描述飞行器周围的流动物理。

利用实验手段研究高超声速稀薄流动中的化学反应效应非常昂贵且难以实施。而分子模型非常适合用来研究化学反应气体流动，因为气相化学反应的基本理论主要与分子层次的过程相关。直接模拟蒙特卡罗(Direct Simulation Monte Carlo,DSMC)方法可用来模拟这些复杂流动，化学反应模块能够在分子层次插入[3]。DSMC方法中的化学反应模型有很多种，最常用的是Bird教授提出的总碰撞能(Total Collision Energy, TCE)模型[3]。不过TCE模型强烈依赖于宏观的化学反应速率系数实验数据。由于高温区域测量数据的缺失和不确定性，高超声速流动模拟中常采用的Arrhenius化学反应速率系数或是从测量的低温平衡化学反应速率系数中插值而来，或是从辐射数据估算而来。对有的反应，不存在实验测量数据，只能从类似的反应中通过近似估算[4]。而且在TCE模型中，从宏观数据到微观反应概率的推导使用了平衡理论，这也使得它可能对分布函数显著偏离平衡形式的气体反应不够精确[5]。为了摆脱这一束缚，发展更高效的方法，基于量子振动模型，Bird教授又提出了新的量子动理学(Quantum Kinetic,QK)模型[5]，用于从微观层次直接计算化学反应气体流动。QK模型不再需要宏观的化学反应速率系数数据，只依赖于碰撞分子的性质，包括可用的碰撞能、离解能和量子化的振动能级[6]。该模型将化学反应过程与碰撞分子的振动模态能量关联起来。这对于深空探测等难以获取可靠实验数据的领域可能是一个值得尝试的选择。

QK模型已经成功吸引了许多国外研究者对DSMC方法的关注[6-9]，但是在国内相关研究工作还处于起步阶段。陈浩等[10]评估了QK模型在氮氧离解复合反应中的表现。近年来国内在DSMC方法方面的研究主要集中在时间步长、并行算法[11-13]、碰撞模型[14]、统计误差[15]以及应用[16-19]等方面。

因此，本文在自研DSMC方法计算程序RariHV中建立QK化学反应模型，通过绝热单元热泳测试和高超声速绕圆柱流动对QK模型的性能进行详细的计算评估。RariHV是中国空气动力研究与发展中心计算空气动力研究所自主研发的一款基于DSMC方法的计算软件，主要用于高超声速稀薄气体流动的气动特性数值模拟，支持三维复杂外形大规模并行计算[14]。

1 量子动理学模型

1.1 离解反应

QK模型中离解反应发生的条件是，如果碰撞能量足够高，超过了离解所需能量，那么反应就会发生。离解反应AB+M→A+B+M(AB代表分子；A和B代表原子；M可以是分子，也可以是原子)发生的条件为

imax>Θd/Θv

(1)

式中：Θd为分子的离解特征温度；Θv为振动特征温度；imax为碰撞能Ec对应的最大振动能级。

(2)

Ec=εtr,AB,M+εv,AB

(3)

式中：为截断取整符号；εtr,AB,M为碰撞对的平动能；εv,AB为分子的振动能;k为Boltzmann常数。

QK模型的一个特点是尽管其执行过程并不需要气体处于平衡态，但是如果假设气体处于平衡态的话，那么可以推导出相应的反应速率kf(T)的解析解。对于可变硬球(Variable Hard Sphere, VHS)模型而言，有

(4)

(5)

(6)

式中：ε为对称因子，如果M分子与AB分子相同，则ε=2，反之ε=1；T为温度；rref为在参考温度Tref时的分子半径；mr为简并质量；ω为黏性温度指数；Q(a,x)=Γ(a,x)/Γ(a)为不完全Gamma函数；zv(T)=1/[1-exp(-Θv/T)]为振动配分函数。

1.2 置换反应

置换反应的现象学过程类似于离解模型。置换反应A+B→C+D(A和C为分子，B和D为原子)发生的概率为

Pr=(1-Ea/Ec)3/2-ω

(7)

式中：Ea为反应活化能，当Ea/k小于Θv时，分母中的求和可近似等于1。

解析的反应速率表达式为

(8)

(9)

本文只计算离解和置换反应。关于复合反应可以参考文献[5]。TCE模型的介绍参见Bird教授的专著[3]，这里不再赘述。

TCE模型将总碰撞能量作为确定反应概率的主要控制参数，没有考虑化学反应对能量依赖的选择性。与TCE模型不同，QK模型将碰前的碰撞对平动能以及所考虑分子的振动能作为碰撞能量参与碰后振动模态能量分配，强调了振动能量在促进反应方面的重要性。这与广义Larsen-Borgnakke模型中的平动-振动能量分配是一致的[7]。

2 绝热单元热泳测试

DSMC方法中碰撞计算只在单元内进行，而化学反应模块是碰撞模块的子模块，因此对化学反应模块的测试可以只考虑一个网格单元。这样做最大程度避免了几何外形、边界条件、网格分区等复杂性所带来的干扰，有利于分析查找问题。分子在单元内自由运动、碰撞，这样的测试称为热泳。具体的测试方法分为2种：一种是平衡测试，另一种是非平衡测试。

所谓平衡测试，就是指并不真正发生化学反应，碰撞对并不真的进行离解、复合或者置换等反应，而是仅仅在程序中对发生碰撞和反应的数目进行计数。反应概率的模拟值可以根据模拟中发生化学反应的碰撞数与总碰撞数的比值来计算。反应速率则根据理论公式计算。单元内能量是不变的，温度也不会改变。反应概率和反应速率存在理论平均值，可以与模拟值进行对比。

反应速率的理论计算公式为[20]

(10)

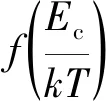
反应概率的理论计算公式为

(11)

化学反应的速率系数数据采用5组分(O2、N2、O、N、NO)19反应空气模型[1]，包括15组离解反应和4组置换反应。需要指出的是，文献中的这些反应速率系数并非实验数据，而是根据QK模型的理论计算结果拟合得到的。采用这套数据是为了方便QK模型和TCE模型的比较。

2.1 平衡反应测试

平衡反应测试在一个边长为10-5m的绝热正方体网格单元内进行。单元的6个面均为镜面反射条件。单元内的初始密度ρ可取为ρ/ρd=107，ρd为特征离解密度，它是温度的函数，但是其变化范围较小，计算结果对其不敏感，通常可以取为常数，如1.30×105kg/m3。单元内布置50 000个 模拟分子，时间步长取为1.52×10-9s。碰撞模型选择VHS模型。内能和平动能之间的松弛采用Larsen-Borgnakke模型，转动和振动松弛碰撞数都取为1。

图1给出了氧气和氮气离解反应的平衡反应速率系数的理论值与模拟值的对比情况。温度范围为5 000～13 000 K，只考虑正向反应。从图中可以看出，反应速率系数随着温度的升高而增加，模拟值与理论值基本吻合。模拟值相比理论值略低，特别是在温度为5 000 K时。这是因为QK模型中离解反应是直接根据碰撞能量以及离解能量的比较来进行的，并不像TCE模型那样计算反应概率，因此，模拟值与理论值无法精确匹配。氮气的离解反应速率系数低于氧气，这是由于氮气离解温度高导致的。图2给出了2组置换反应的平衡反应速率系数随温度的变化情况，模拟值与理论值在所有温度下都高度吻合。本文对其余15组反应也进行了相应的测试，结果都吻合良好，限于文章篇幅，这里没有给出。

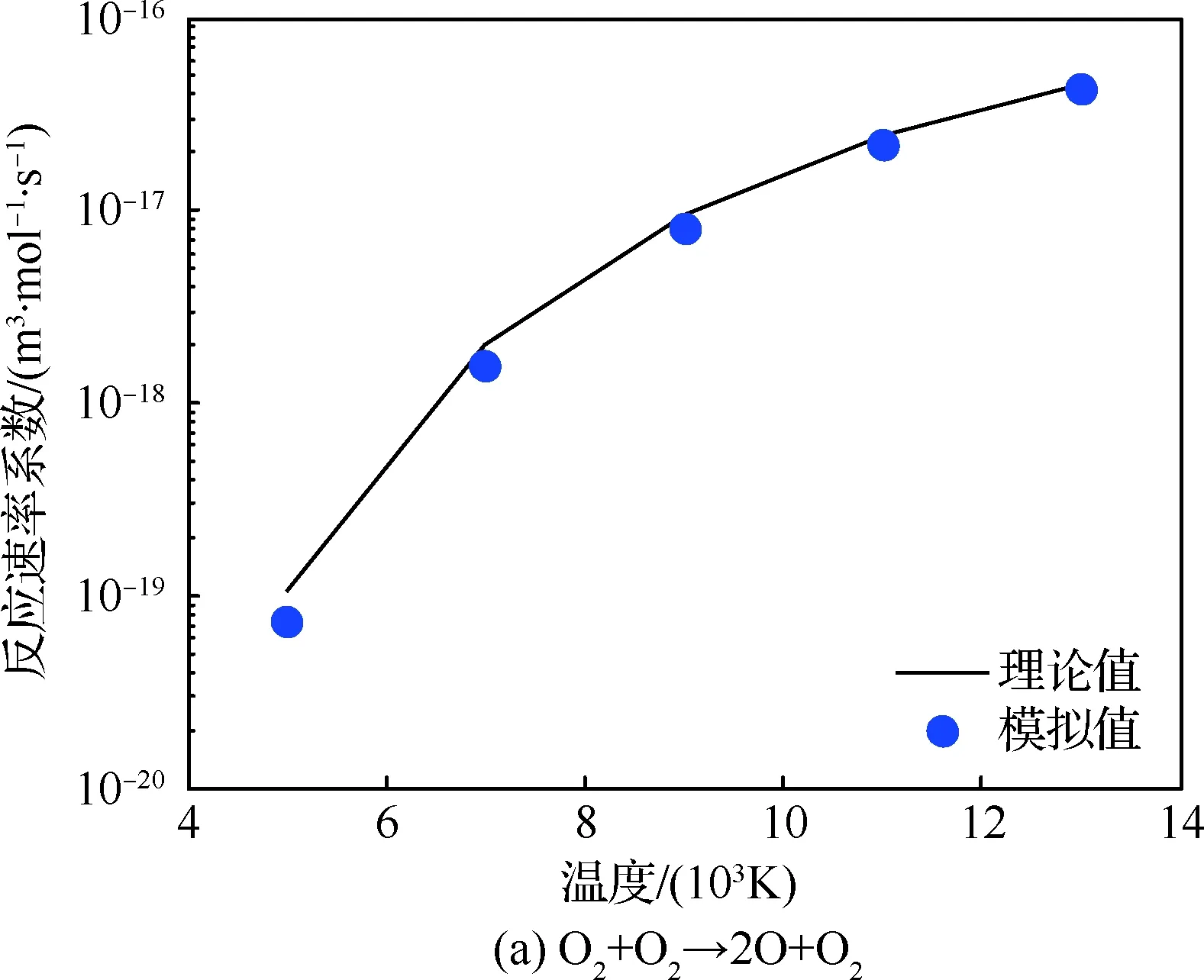
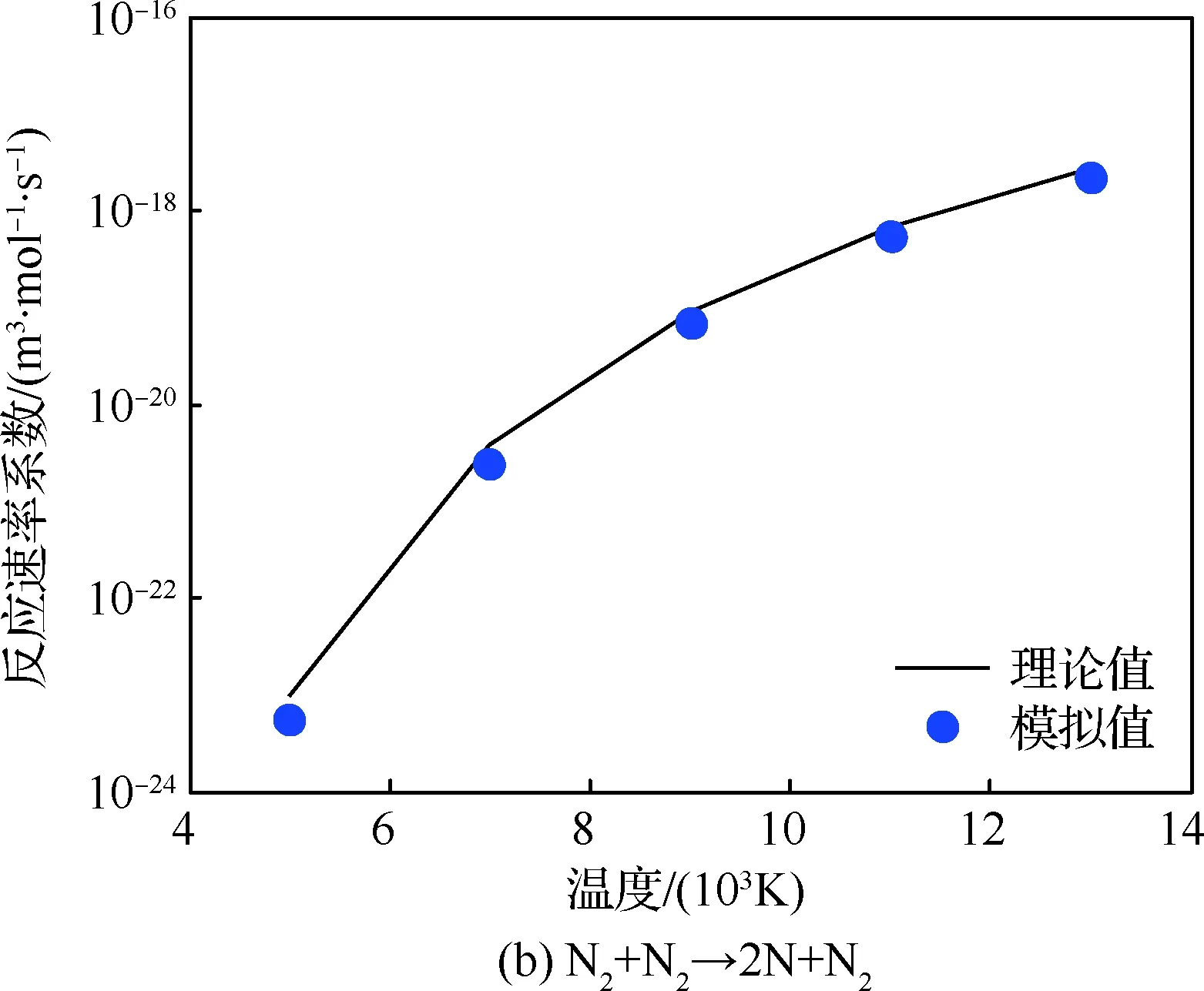
图1 离解反应的平衡反应速率系数Fig.1 Equilibrium reaction rate coefficient for dissociation reactions

图2 置换反应的平衡反应速率系数Fig.2 Equilibrium reaction rate coefficient for exchange reactions

平衡反应的测试结果表明，在一定精度范围内，QK模型可以给出准确的化学反应速率系数。

2.2 非平衡反应测试

非平衡反应测试采用Haas和Mcdonald[21]提出的方法。该方法可以求得反应过程中单元内各化学组分的浓度变化以及宏观温度随时间变化的解析解，以便与模拟解对比。表1是测试条件，其余条件与平衡反应测试中相同。

工况2～4对全部19组空气反应同时测试。组分均为21%的氧气和79%的氮气，仅初始温度和数密度不同。初始的单元温度分别是30 000、20 000、10 000 K。图4给出了不同工况下组分浓度与单元温度随时间的变化。随着温度的降低，氮气的离解变弱，平衡后的组分浓度分别约为20%、50%和76%。氧气离解比较充分，但离解的速度也随温度的降低而变慢。3个工况均以吸热反应为主，单元温度随时间不断下降。除工况3中氮气分子和氮原子的组分浓度与理论解有一定偏差外，QK模型预测的组分浓度及单元温度随时间的变化与理论解基本吻合。

表1 非平衡反应测试条件Table 1 Test conditions of non equilibrium reactions

图3 组分浓度和单元温度随时间的变化(工况1)Fig.3 Temporal evolution of species concentrations and temperatures (Case 1)

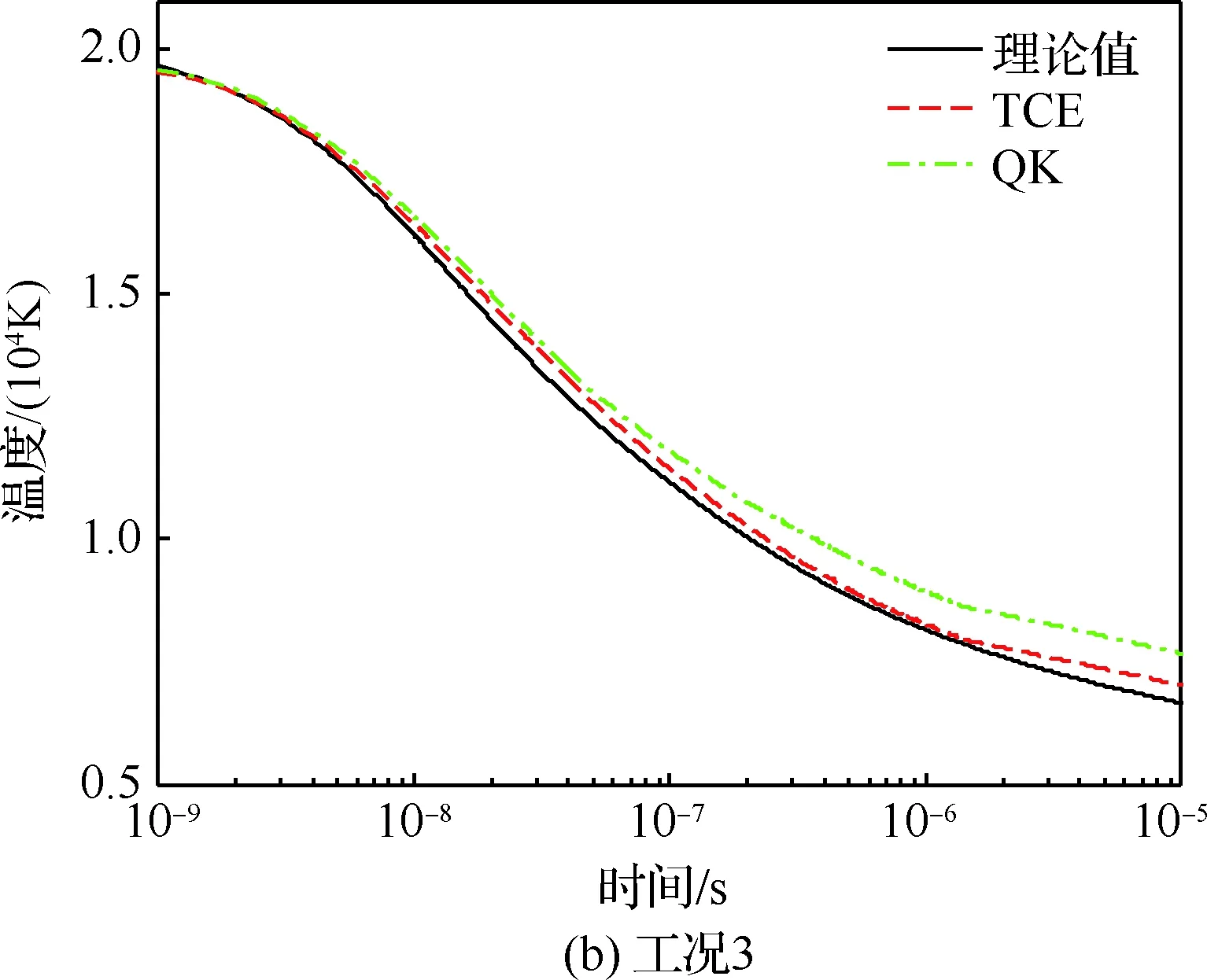
图4 不同工况下组分浓度和单元温度随时间的变化Fig.4 Temporal evolution of species concentrations and temperatures under different cases

非平衡反应测试的结果表明，在一定精度范围内，QK模型可以准确预测化学反应热松弛过程。

3 数值算例

为了进一步测试QK模型的应用能力，本文模拟了高超声速绕圆柱流动。圆柱直径为2 m。来流由78.85%的氮气和21.15%的氧气组成，来流数密度为1.43×1020m-3。来流克努森数约为0.004。来流马赫数为24.85，迎角为0°。来流温度为187 K，圆柱表面温度为1 000 K，完全漫反射，不考虑催化。更详细的信息参见文献[1]。

图5给出了不同模型预测的温度场的比较。图5(a)是无化学反应和QK模型结果的比较，图5(b)是TCE模型和QK模型结果的比较。从图中可以看出，TCE模型和QK模型计算的流场温度分布吻合良好。与无化学反应的计算结果相比，尽管来流克努森数较小，属于近连续流，但由于化学反应，流场最高温度降低了约3 800 K。

图6给出了驻点线上的平动、转动及振动温度分布。从图中可以看出，温度非平衡效应十分明显。图中各线型(直线、虚线及点划线)分别代表本文模拟值，与之相对应的各符号(方框、菱形及圆形)为文献[1]结果。弓形激波位于圆柱前约25 cm处。气体经过激波后温度迅速上升，然后在近壁面处下降。平动、转动和振动温度的峰值分别为约20 000、13 000、9 000 K。从图中可以看出，除了转动温度的峰值略低之外，本文计算结果与文献[1]结果吻合良好。

图5 不同模型温度场的对比Fig.5 Comparison of temperature contours by different models

图7给出了驻点线上5组分的数密度分布情况。图中各线型为本文模拟值，与之相对应的各符号为文献[1]结果。从图中可以看出，QK模型可以准确捕捉到化学反应流场中的组分分布。

图6 驻点线上温度对比Fig.6 Comparison of temperatures along stagnation line

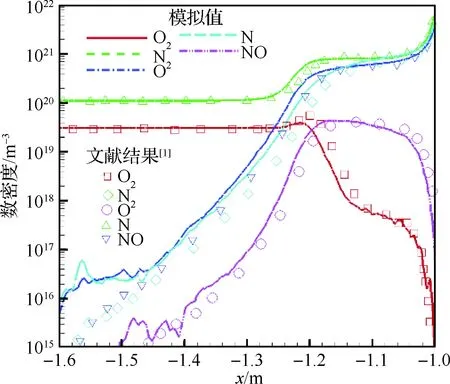
图7 驻点线上组分数密度对比Fig.7 Comparison of number densities along stagnation line

4 结 论

本文在自研DSMC软件中实现了新的量子动理学化学反应模型，并对其进行了计算精度的测试，得到以下初步结论：

1) QK模型在绝热单元平衡和非平衡热泳中表现良好，模拟结果与理论解吻合。这表明，QK模型可以给出准确的化学反应平衡速率并预测化学反应非平衡过程。

2) 本文将QK模型应用于高超声速绕圆柱计算中，所得计算结果无论是宏观的驻点线上温度，还是微观的组分数密度分布等，都与文献[1]结果吻合良好。这表明QK模型具有计算真实高超声速化学反应流动的能力。

从本文初步的评估来看，QK模型具有优良的特性，可应用于高超声速化学反应流动计算。QK模型不依赖宏观的化学反应速率数据，未来有希望应用于深空探测等领域，当然其性能也还需要进一步的考察和检验。

下一步，将应用QK模型进行火星探测器稀薄气动特性的计算。