修正Camassa-Holm方程的可积推广及其可积性质
洪建彬,吴红霞
(集美大学理学院,福建 厦门 361021)
0 引言
修正的Camassa-Holm(modified Camassa-Holm,mCH)方程最初以一种新的可积系统被研究[1-3]。之后,文献[4-5]重新发现并推导出该方程。文献[1]把三哈密顿结构运用于mKdV方程的双哈密顿形式中,从而推出mCH方程。
众所周知,mCH方程在很多领域都有重要的应用。例如,在物理学上,该方程描述是在浅水波上单方向传播时的相互作用,其中u是自由液面高度,文献[6]从二维流体力学的表面波推导出该方程;在几何学上,该方程也来自一种内在的(弧线保留)流在欧几里得几何[7]不变的平面曲线。从此,mCH方程引起了人们的关注。研究表明,mCH方程与CH方程有很多相似的可积性质,该方程具有Lax对和达布变换[8]、爆破波和peakon[7]、Well-posedness[9]、双哈密顿结构[1]、无穷守恒律、孤子解[10]。然而,mCH方程与CH方程的可积性质[11]不同之处在于mCH方程具有高阶非线性,所以mCH方程具有包括爆破波和multi-peakon动态等新的特点。而且,无论mCH方程在有无界条件下,该方程都具有光滑的亮孤子解[12]。
作为孤子方程的可积推广,带源的孤子方程(soliton equations with self-consistent sources,SESCS)在很多领域如等离子体、固体物理和流体力学等均有广泛的应用。例如,带源KdV方程描述了长短毛细-重力波的相互作用[13]。2010年,文献[14]考察了带自相容源的Camassa-Holm方程(Camassa-Holm equation with self-consistent sources,CHESCS)在浅水中不同孤立波的相互作用,同时构造了CHESCS及其相应Lax对、无穷守恒律和互反变换,也给出了CHESCS的一些新解,例如soli-ton、negaton、positon和单peakon解。
已有学者对CHESCS进行了研究,但对mCHESCS研究过少。由于CH方程具有二次非线性,而mCH方程具有三次非线性,这必将使得mCHESCS的构造要比CHESCS的更复杂。本文主要研究mCH方程
(1)
的推广问题,这里u(x,t)是与空间变量x和时间变量t有关的函数。本文主要研究mCHESCS的构造和求解,同时,mCHESCS的Lax对、无穷守恒律和互反变换等一些可积性质也会相继给出。
1 带源mCH方程及其Lax对
1.1 带源mCH方程
众所周知,mCH方程(1)Lax对中的空间部分为
(2)
时间部分为
(3)
这里λ为谱参数。
利用式(2)和式(3)的相容性可推导出mCH方程(1)。以下为mCH方程的双哈密顿形式
(4)

对于n个不同的实数λj,考虑以下谱问题
(5)
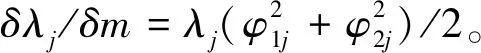
(6)
其中φ1j和φ2j由式(5)确定。由式(6)可推导出mCHESCS
(7)
φ1jx=-φ1j/2+λjmφ2j/2,φ2jx=-λjmφ1j/2+φ2j/2,j=1,…,N。
(8)
在式(8)条件下,mCHESCS可以重写为
(9)
1.2 带源mCH方程的Lax对
下面推导出mCHESCS的Lax对。假设mCHESCS有如下的Lax对
(10)
(11)

(12)
有
λm(B3+C3)/[2(λ-λj)]+λm(B4+C4)/2+λ2m(B5+C5)/2}=0,
(13)
B3/(λ-λj)+B4+λB5],
(14)
(15)

(16)
(17)
-A4x+m(B0+C0)/2+mλj(B2+C2)/2=0,-A5x+m(B2+C2)/2+m(B4+C4)/2=0,
(18)
B5+C5=0,A5=0,
(19)
(20)
(21)
B4x+mA0+λjmA2+B4=0,mt=2(B5x+mA2+mA4+B5)=0,
(22)
(23)
(24)
C4x+mA0+λjmA2-C4=0,mt=-2(C5x+mA2+mA4-C5)=0。
(25)
(26)
(27)

2 带源mCH方程的无穷守恒律
基于mCHESCS的Lax形式,构造出带源mCH方程的无穷守恒律。令Γ=φ2/φ1,其中φ1和φ2是由方程(26)和(27)所确定。由式(26)知道Γ满足Riccati方程[15]
Γx=-λm(Γ)2/2+Γ-λm/2。
(28)
由方程(26)和(27)可得出
(lnφ1)x=-1/2+λmΓ/2, (lnφ1)t=V11+V12Γ,
(29)
其中,
(30)
注意到方程(29)的相容性条件,
θt=Fx,
(31)
其中,θ=mΓ,
(32)
其中,θ为守恒密度,F为伴随通量。以下通过两种正负不同的λ的阶展开Γ,从而得到守恒密度的显式表达式。
第一种以λ负阶形式展开Γ,
(33)
其中Γj,θj和Fj(j=0,1,2,…)是与x,t有关的函数。
将式(33)代入式(28)并比较λ的系数,得到
Γ0=I, I2=-1, Γ1=1/m,
(34)
以及与Γj有关的递推公式:
(35)
将式(33)~式(35)代入式(32),分别得到方程(9)的守恒密度和伴随通量,
(36)
其中Γj由式(34)和式(35)所确定。
第二种Γ的展开是以λ的正阶展开
(37)
将式(37)代入式(28)并比较λ的系数,得到
(38)
将式(37)和式(38)代入式(32),同样得到
θ2j=0,F2j=0,j≥0,
(39)
以及
(40)
其中Γ2j+1由以下递推公式所定义
(41)
3 带源的mCH方程的互反变换
方程(7)可重写为
(42)
方程(42)给出封闭的1-form
(43)
以下通过文献[8]的关系定义互反变换(x,t)→(y,s)
(44)
以及
(45)
进而mCHESCS(7)可转为以下新的形式
(46)
mφ1jy=-φ1j/2+λjmφ2j/2,mφ2jy=-λjmφ1j/2+φ2j/2,
(47)
且u与m有关,即
(48)
称式(46)、式(47)和式(48)的系统为相伴的mCHESCS(associated mCHESCS,AmCHESCS)。基于互反变换(45),谱问题(26)的空间部分可转变为薛定谔中的谱问题
φ2yy=-λ2φ2/4+Uφ2,
(49)
以及
U=1/(4m2)-my/(2m2)。
(50)
同样,谱问题(27)的时间部分也可转为
(51)
且
V=-2(u+ux)=-2(u+muy)。
(52)
由式(49)和式(51)的相容性,可得出
(53)
不难发现,式(53)为负阶的KdVESCS(negative order KdVESCS,NKdVESCS)。
令ρ=φ2y/φ2。由方程(49)发现,ρ满足Riccati方程
ρy=-λ2/4+U-ρ2。
(54)
将式(50)代入式(54),得到
m=1/(2ρ)|λ=0=φ2(y,s,λ)/(2φ2y(y,s,λ))|λ=0。
(55)
注意到式(55)可用来求AmCHESCS的multi-soliton、multi-negaton和multi-positon解。
4 带源的mCH方程的解
4.1 带源的mCH方程的multi-soliton解
由文献[8],注意到负阶的KdV方程的N-soliton已给出
(56)
其相应特征函数
φ=W(f1,f2,…,fN,eξj)/W(f1,f2,…,fN),
(57)
其中W是N个函数f1,f2,…,fN的朗斯基行列式。这里函数fj由以下
(58)
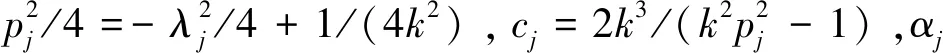
根据文献[16]和常数变易法,得到NKdVESCS(53)的N-soliton解
(59)

(60)
(61)
注意到φ1和φ2的渐近性质分别为
(62)

(63)
进一步,把式(63)代入式(48)中,得到以下mCHESCS的N-soliton解
(64)
其中α为任意常数且
(65)
特别地,当N=1,从方程(64),得到如下mCHESCS的one-soliton解的参数形式
(66)
4.2 带源的mCH方程的multi-negaton解

αj(s)=yj(pj)
(67)
αN+j(s)=(pN+j-pj)ej(s)/pN+j+yj(pN+j),j=1,2,…,N,
(68)
其中:yj(k)是与k有关的渐近函数;ej(s)是与s有关的任意函数。
通过泰勒展开式和假设pN+j→pj,j=1,2,…,N,得到如下NKdVESCS(53)的N-negaton解
(69)

(70)
与mCHESCS的N-soliton解的做法相似,得到如下mCHESCS的N-negaton解
(71)
其中α是任意可积常数且
(72)
特别地,当N=1,从方程(71),得到mCHESCS的one-negaton解
(73)

4.3 带源的mCH的multi-positon解
当N=0时,令V=-2k和U=1/(4k2)为NKdVESCS(53)的解,从方程(49)和式(51),得到
φ2yy=(-λ2/4+1/(4k2))φ2,φ2s=-2kφ2/λ2。
(74)
注意到-λ2/4+1/(4k2)<0,得到如下(74)的解
fj=sinξj,
(75)

与N-negaton解的做法相似,如下得到NKdVESCS(53)的N-positon解
(76)

(77)
由式(77)知道如下φ1和φ2的渐近性质
(78)
其中I2=-1。类似地,得到
(79)
与N-negaton解的做法类似,得到如下mCHESCS的N-positons解
(80)
其中α是任意可积常数且
(81)
特别地,当N=1时,从方程(80),得到如下mCHESCS的one-positon解
(82)

5 结语
本文推导出mCHESCS及其相应的Lax对。此外,构造出该方程的互反变换和无穷守恒律。基于达布变换和常数变异法,得到mCHESCS的N-soliton、N-negaton和N-positon解。众所周知,由于mCH方程存在peakon解,那么mCHESCS是否也有peakon解?这是一个令人感兴趣的问题,在以后的研究中,笔者将会做进一步的探讨。

