马尔可夫调制的双分数布朗运动模型下亚式期权定价*
宋瑞丽,李 旭,王 伟
(南京财经大学 应用数学学院,南京 210023)
0 引 言
本文利用马尔可夫调制的双分数布朗运动来描述B-S市场中风险资产的价格动态,利用马尔可夫链刻画经济周期中的结构变化,通过亚式期权所满足的概率密度转移函数,采用测度变换技巧将实际概率测度变换成等价鞅测度,利用风险中性定价原理分别得到具有固定执行价格的亚式看涨和看跌期权的定价公式,且可基于双分数布朗运动亚式期权定价模型对分数布朗运动的几何平均亚式期权定价模型进行推广。
1 模型假设
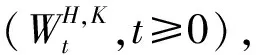
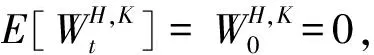

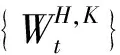
假定在无套利金融市场中有一种债券和一种股票,它们的价格过程分别满足如下随机微分方程:
其中,r:=(r1,r2,…,rN)∈RN,rt:=[r,Xt]表示市场的利率;σ:=(σ1,σ2,…,σN)∈RN,σt:=[σ,Xt]表示股票的波动率;μ:=(μ1,μ2,…,μN)∈RN,μt:=μ,Xt表示股票的平均回报率;·,·表示内积均依赖于{Xt}t∈Γ的状态;是具有Markov调制的双分数布朗运动,存在新的等价-鞅测度Q和满足

是概率测度Q下的双分数布朗运动,并且有
(1)
对任意0 (2) 对于固定执行价格的几何平均亚式看涨期权,它的损益为 (3) (XtYt-K)+ (4) 注意到当前时刻是t时刻,则Xt是已知的,由式(2)可得: e(r*(t)+Zt) (5) 其中, 根据双分数布朗运动的定义及性质可得: 由分数型等距公式[12]可得: 其中, 那么 (6) 令ut表示几何平均亚式看涨期权的损益在当前时刻的贴现值,则由式(3)(4)可得: (7) (8) 定理1 具有固定执行价格的几何平均亚式看涨期权价格为 其中, 证明根据式(6)中Zt的分布和式(8)确定ut的分布: 随机变量ut的期望为 (9) (10) 把式(10)代入式(9)可得: (11) Ct=E[ut|Gt,T]= 几何平均亚式看跌期权的损益为 (12) 定理2 具有固定执行价格的几何平均亚式看跌期权价格为 其中, 证明同理,由式(6)中Zt的分布和式(8)可得损益νt的条件分布: 随机变量νt的期望为 (13) 所以将式(13)代入看跌期权的价格公式,可得: (14) Pt=E[vt|Gt,T]= 通过等价-拟鞅测度变换,在市场利率、股票波动率和股票回报率均受Markov链调制的情形下得到了双分数B-S市场的固定价格几何平均亚式期权定价公式,将经典的测度变换方法与拟鞅相结合,并推广到双分数布朗运动市场环境。在一定程度上,相对多数只研究分数布朗运动或市场利率、股票波动率和股票回报率均为常数的模型有所改进。对于Markov链调制的受双分数布朗运动驱动的浮动执行价格的亚式期权定价公式有待进一步研究。2 具有固定执行价格的亚式看涨、看跌期权定价公式

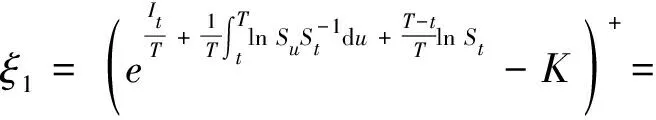
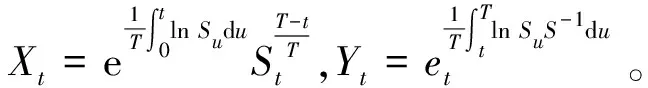
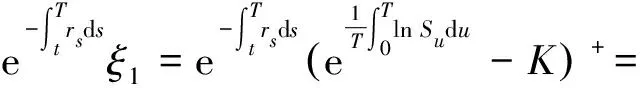
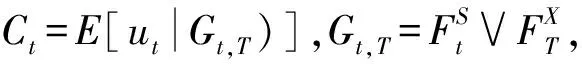
2.1 具有固定执行价格的亚式看涨期权定价公式
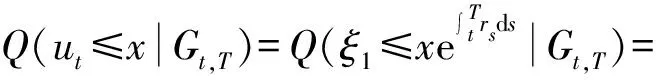
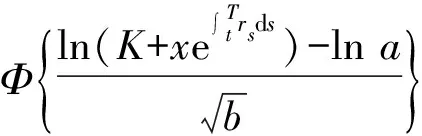
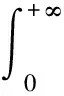
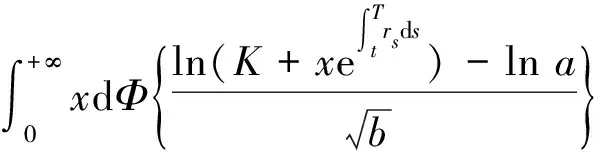
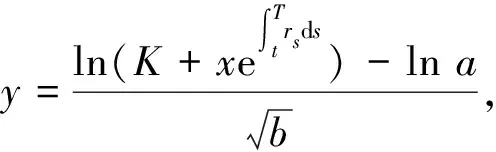
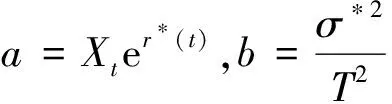
2.2 具有固定执行价格的亚式看跌期权定价公式
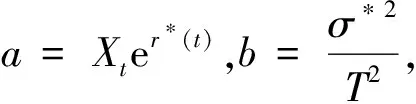
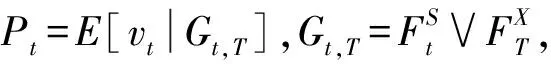
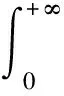
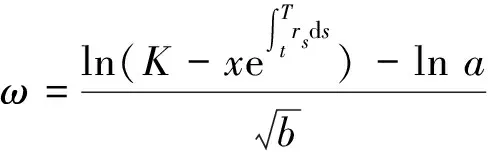
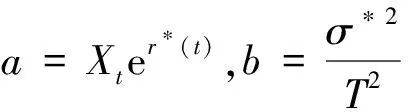
3 结 论

