软弱围岩浅埋小净距隧道合理净距影响因素探讨

李松, 陈秋南, 黄林华

(1.湖南科技学院 土木与环境工程学院, 湖南 永州 425000；2.湖南科技大学 土木工程学院)

当前，小净距隧道成为高速公路和高速铁路中常见的结构形式，其上下行导洞开挖对围岩稳定的影响成为重要的研究内容。近年来，小净距隧道施工关键技术一直得到较多学者的研究，针对小净距隧道合理净距的讨论也有比较多的成果，研究者们大多通过数值模拟分析中间岩柱塑性区的方法来确定合理净距，有研究者采用屈服接近度、中间岩柱应力应变等方法来确定合理净距，也有学者尝试推导简化的解析解。现行隧道设计规范中以隧道跨度和围岩等级两个因素来界定小净距隧道与分离式隧道，考虑的因素较少，特别是大断面小净距隧道的安全净距没有明确规定，但是，决定小净距隧道合理净距的因素有很多，目前无论哪一种研究手段对于这个问题的研究都具有一定局限性，很多研究成果试图建立隧道跨度与合理净距之间的关系，但是单纯建立隧道跨度与合理净距之间的关系参考意义有限。该文将考虑不同跨度、埋深、高度和初始地应力等条件，进行数值模拟对比分析，研究各因素对小净距隧道合理净距的影响。

1 不同类型隧道的合理净距

1.1 模型建立

JTG D70-2004《公路隧道设计规范》提供了两车道和三车道公路隧道标准内轮廓断面图纸，TB 10020-2009《高速铁路设计规范》中也提供了250 km/h和350 km/h的高铁隧道标准内轮廓断面图纸，实际设计时在满足隧道建筑限界要求的条件下设计成果一般与标准图纸略有差异，以表1中不同断面隧道作为此次数值计算的对象，隧道开挖断面参数来源于实际工程设计图纸。

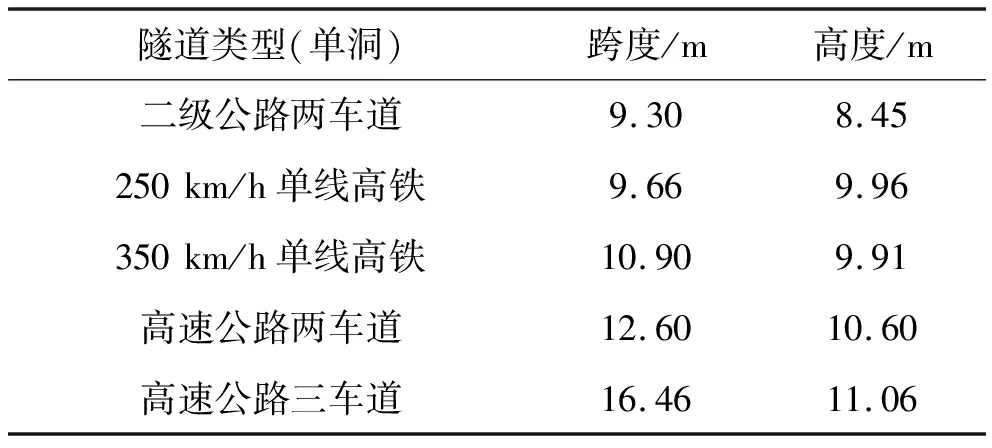
表1 隧道开挖断面参数

注：高度为仰拱底至拱顶的高差。

通过FLAC3D建立Ⅴ级围岩隧道模型，强度准则为摩尔-库仑准则，其围岩计算参数见表2。

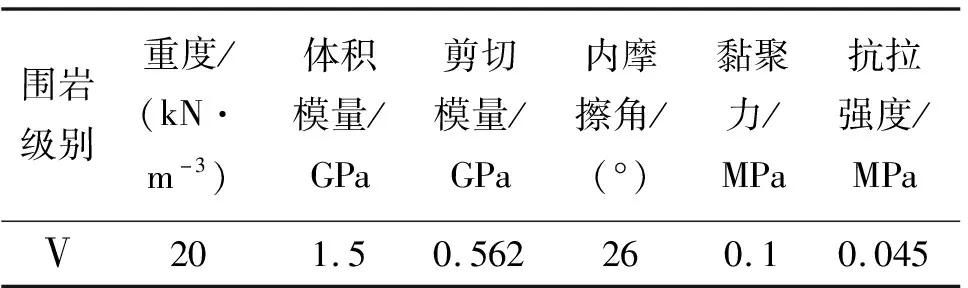
表2 围岩计算参数

按JTG D70-2004《公路隧道设计规范》，浅埋隧道和深埋隧道的分界深度与隧道的跨度有关，表1中两车道二级公路隧道在Ⅴ级围岩中的分界深度约26 m，据此分析，其余隧道分界深度大于26 m，故将模型隧道埋深统一取25 m，所有隧道模型理论上均为浅埋隧道。

模型左右边界200 m，上下边界100 m，进深1 m。

初始地应力由自重形成，侧压力系数(水平地应力系数)λ为0.5。

考虑最不利情形，所有模型均不施加支护结构，一次性开挖。

为了方便叙述，下文称本组模型中的高速公路两车道隧道模型为模型1。

模型网格在以下分析结果中列出，此处不再单列。

1.2 计算结果

对各类型隧道建立不同净距的小净距隧道模型，以中间岩柱塑性区不贯通为安全净距，各类隧道塑性区分布特征及合理净距见表3。

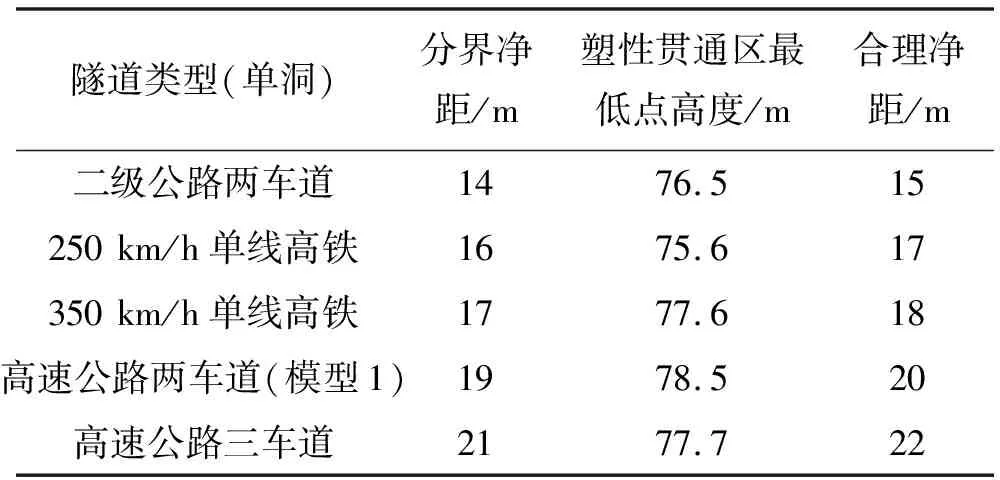
表3 各类隧道塑性区特征及合理净距

注：① 分界净距为中间岩柱塑性区贯通条件下的最大净距；② 塑性贯通区最低点高度为模型底部至塑性贯通区域最低点的距离。

1.3 结果分析

图1为不同类型隧道的跨度与合理净距的关系，图2为二级公路两车道隧道和250 km/h单线高铁隧道分界净距时的塑性区。计算结果表明：随着隧道跨度的增大，合理净距也随之增大，但是不同类型隧道的跨度与合理净距之间并非线性关系，比较二级公路两车道隧道和250 km/h单线高铁隧道合理净距可看出，把合理净距表示为跨度的倍数是不合适的。从塑性区开展深度来看，贯通区的最低点相差不大，但是计算过程中隧道的净距在增大，所以中间岩柱的塑性区开展方向的角度也在增大，隧道设计过程中确定围岩压力时应当对滑动破裂角进行修正。

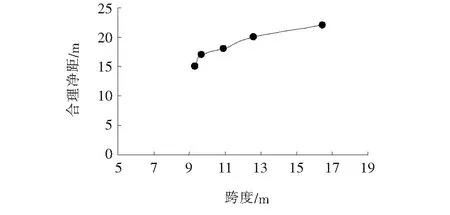
图1 隧道跨度与合理净距关系

2 埋深对合理净距的影响

2.1 模型建立

隧道类型选高速公路两车道隧道，围岩等级为Ⅴ级围岩，参数见表1、2，维持模型1下边界不变，增加上边界高度分别建立25、27、29、31、33 m共5种埋深的隧道模型，初始地应力及开挖支护见模型1。

2.2 计算结果

对各种埋深的小净距隧道建立不同净距的模型，以中间岩柱塑性区不贯通为安全净距，各种埋深条件下塑性区分布特征及合理净距见表4。

2.3 结果分析

图3为隧道埋深与合理净距的关系，图4为埋深分别为27、33 m的围岩塑性区。计算结果表明：隧道埋深与合理净距大致呈线性关系，埋深越大，合理净距也越大，塑性贯通区的高度随埋深增大而增大。隧道埋深增大则围岩压力增大，安全净距也随之加大，在可预见的范围内，小净距隧道合理净距将按此规律变化，文献[9]确定的浅埋隧道围岩压力计算方法与该数值模拟结果不矛盾，而一般情况下隧道埋深大围岩更稳定，故用此数值方法来确定深埋小净距隧道合理净距则不合理，更何况深部围岩的力学参数和初始地应力与浅部围岩有较大差异。摩尔-库仑强度准则由大小主应力决定围岩剪切破裂角，计算结果也表明中间岩柱塑性区开展方向的角度随埋深增大而增大，所以进行小净距隧道围岩压力设计计算时，也应该考虑埋深对破裂角的影响。

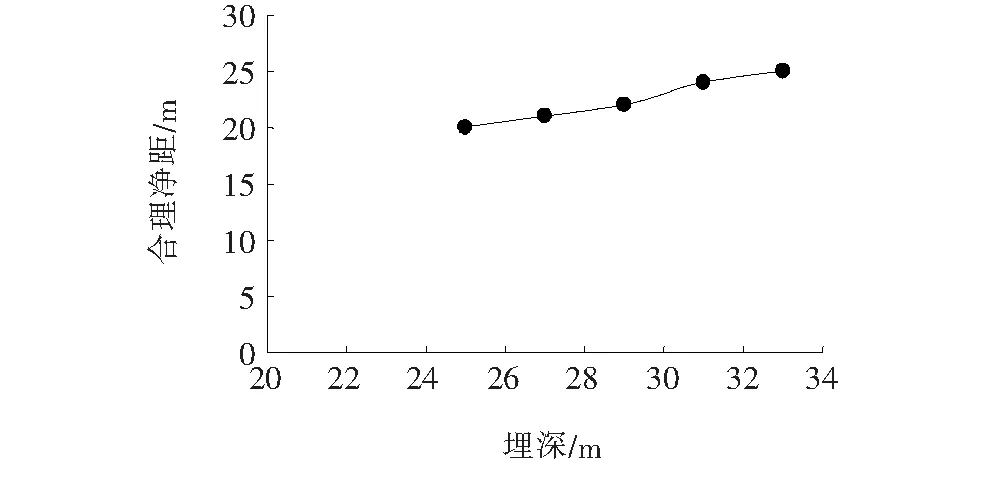
图3 隧道埋深与合理净距的关系

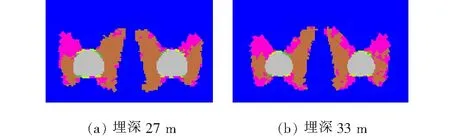
图4 围岩塑性区分布

3 初始地应力对合理净距的影响

3.1 模型建立

隧道类型选高速公路两车道隧道，围岩等级为Ⅴ级围岩，参数见表1、2，隧道埋深取25 m，分别建立侧压力系数λ=0.5、0.45、0.4、0.35共4种隧道模型，模型边界及开挖支护同模型1。

3.2 计算结果

对不同侧压力系数的小净距隧道建立不同净距的模型，以中间岩柱塑性区不贯通为安全净距，各条件下塑性区分布特征及合理净距见表5。

表5 不同初始地应力条件下隧道塑性区特征及合理净距

3.3 结果分析

图5为侧压力系数与隧道合理净距的关系，图6为λ=0.4和λ=0.35时合理净距模型的围岩塑性区分布。随着侧压力系数减小，合理净距随之增大，中间岩柱上部塑性贯通区高度随之增高，而中间岩柱拱脚处塑性区开展明显比拱腰处深，λ=0.35时，隧道间距达到28 m时拱脚处塑性区仍然贯通。侧压力系数决定了自重初始应力场，以上计算结果表明侧压力系数对围岩的稳定性影响很大，而文献[9]推荐的Ⅴ级围岩侧压力系数为0.3～0.5，故设计小净距隧道时选择合理净距和支护结构时应当重视侧压力系数的取值。

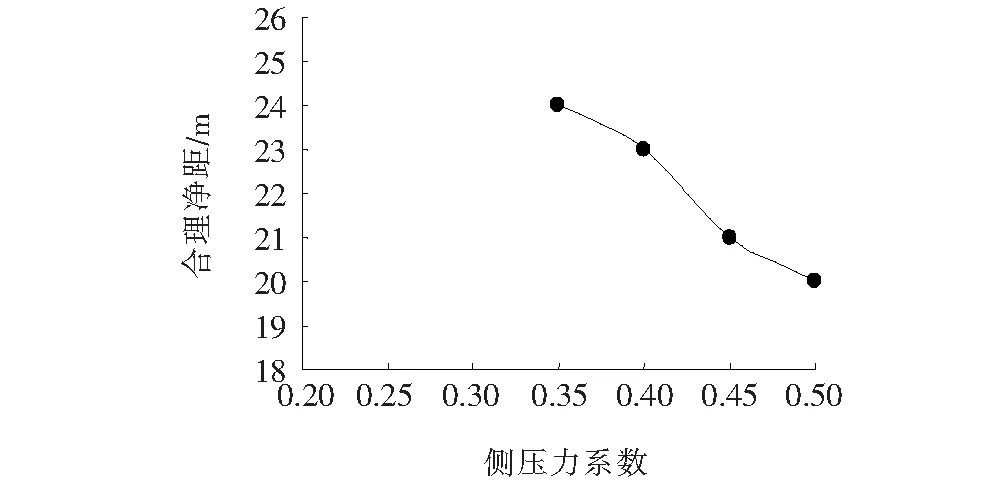
图5 侧压力系数与合理净距的关系

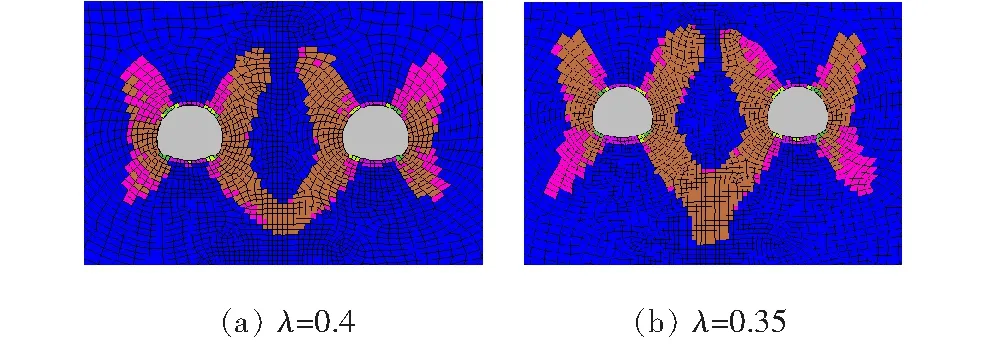
图6 围岩塑性区分布

4 隧道高度对合理净距的影响

4.1 模型建立

参照高速公路两车道隧道的跨度和高度，建立跨度为12.6 m，高度分别为10.6、11.6、12.6、13.6 m共4种不同高度的隧道模型，为方便模型建立，隧道边墙为直墙，不带仰拱。

模型为Ⅴ级围岩，参数见表2，隧道埋深均为25 m，侧压力系数λ=0.5，模型边界、初始地应力及开挖支护同模型1。

4.2 计算结果

对不同高度的小净距隧道建立不同净距的模型，以中间岩柱塑性区不贯通为安全净距，各条件下塑性区分布特征及合理净距见表6。

表6 不同高度隧道塑性区特征及合理净距

4.3 结果分析

图7为隧道高度与合理净距的关系，图8为隧道高度10.6、13.6 m时的围岩塑性区。埋深不变的条件下，隧道高度与隧道埋深有较强的线性关系，大致上高度增加1 m，合理净距增加2 m，这一结果与二级公路两车道隧道和250 km/h单线高铁隧道合理净距的计算结果相似。隧道高度为10.6 m时的计算结果与表2中计算结果有出入，表2中二级公路两车道隧道合理净距计算结果为20 m，此处相同跨度和高度的隧道模型计算结果为23 m，说明断面形状对围岩应力场的重新分布有明显的影响，从而对合理净距有显著的影响。中间岩柱塑性贯通区高度随隧道高度增加而增加，同样表明围岩塑性区开展方向的角度随高度增大而增大，设计计算围岩压力时应当考虑隧道断面形状和高度的影响。

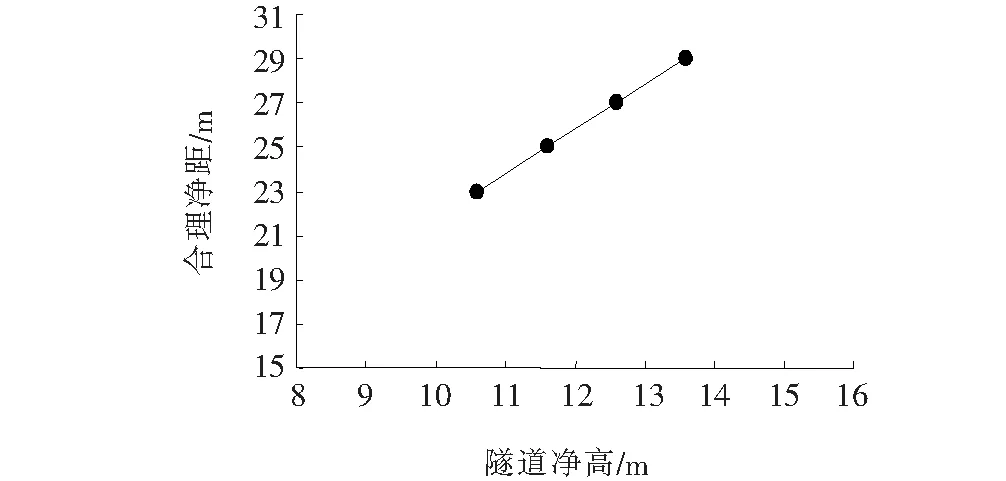
图7 隧道高度与合理净距的关系

图8 围岩塑性区

5 偏压对合理净距的影响

5.1 模型建立

隧道类型为高速公路两车道隧道，围岩等级为Ⅴ级，参数见表1、2，左右隧道拱顶连线中点埋深为25 m，分别建立坡比1/8、1/6、1/4、1/3、1/2共5种偏压隧道模型，模型下边界及开挖支护同模型1。

5.2 计算结果及分析

以中间岩柱塑性区不贯通为安全净距判定标准，除坡比1/2外，其他偏压条件下的合理净距均为20～21 m，图9为20 m净距时各偏压条件下塑性区分布情况。

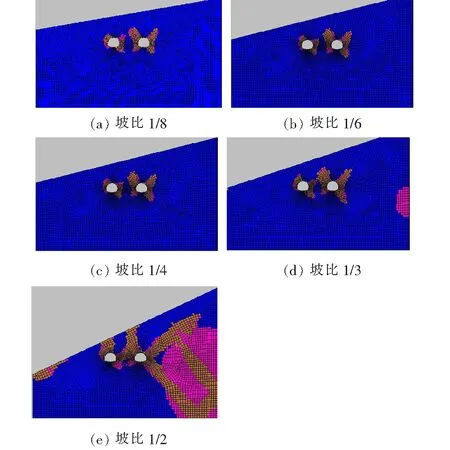
图9 围岩塑性区分布(净距20 m)

计算结果表明：从中间岩柱稳定性的角度来分析，偏压对合理净距的影响并不明显，但对围岩塑性区的影响很大，随着偏压程度增加，埋深大的那一侧隧道围岩塑性区开展范围增大，当偏压达到一定程度，中间岩柱、边坡及埋深大的一侧隧道围岩稳定性的危害急剧增大。

6 结论

通过对不同跨度、埋深、高度和初始地应力等条件下的软弱围岩浅埋小净距隧道进行数值模拟分析，得到以下结论：

(1)跨度作为小净距隧道合理净距的重要影响因素，并不应该成为唯一决定性因素，小净距隧道的合理净距与隧道埋深、地应力和隧道高度等条件密切相关。

(2)小净距隧道合理净距随隧道埋深加大而逐步增大，在可预见的范围内，小净距隧道合理净距将按此规律变化下去，这与工程实际情况不一致，所以在进行数值模拟确定深埋小净距隧道合理净距时，应当改变计算手段。

(3)围岩侧压力系数减小，小净距隧道合理净距随之增大，而且中间岩柱拱脚处塑性贯通区甚至先于拱腰处出现，故设计小净距隧道时应当高度重视侧压力系数的取值。

(4)隧道高度对小净距隧道合理净距也有一定的影响，相同埋深相同跨度的小净距隧道，其合理净距随高度增大而增大。

(5)隧道埋深、侧压力系数及隧道断面形状等因素影响了围岩初始应力场和重分布应力场，小净距隧道中间岩柱塑性区开展方向的角度也随之改变，设计计算围岩压力时应当考虑这些因素。

(6)偏压对合理净距的影响并不明显，但对围岩压力塑性区的影响很大，当偏压达到一定程度，中间岩柱、边坡及埋深大的一侧隧道围岩稳定性的危害急剧增大。