基于自然选择策略的PSO-BP神经网络的滑坡可靠性评价方法
王彪龙,孟凡利,曾超,郭将,刘晓*
(1.中国地质大学(武汉)教育部长江三峡库区地质灾害研究中心,湖北 武汉 430074;2.中交第二公路勘察设计研究院有限公司)
1 引言
在边(斜)坡稳定性评价中,由于岩土体参数(如黏聚力c、内摩擦角φ等)存在着不确定性,而传统的确定性分析往往难以满足实际的需要,所以应综合考虑各种不确定性因素,对其进行可靠性分析。传统的可靠性求解方法有蒙特卡洛法(Monte Carlo Simulation, MCS)、一次二阶矩法(First Order Second Moment Method, FOSM)等,其中蒙特卡洛法需大量抽样,而每一次抽样均需对应一次完整的边坡稳定性分析隐式过程,因此总体计算量大,但其优点在于概念明确,可用来检验其他计算方法的精度。
响应面法包括多项式函数、支持向量机、BP(Back Propagation)神经网络等。其中BP神经网络具有较高的拟合精度和自适应性,在函数拟合、数据预测方面运用广泛。但是,基本BP神经网络容易陷入局部极值点,同时收敛速度也较慢。为此,众多学者对基本BP神经网络进行了改进,如将粒子群算法用于BP神经网络权值和阈值的寻优,主要包括:① 运用粒子群算法先优化得到一组较好的权值和阈值,作为BP神经网络的初始权值和阈值,而后采用BP神经网络内置的最速梯度下降法继续寻优,得到最优权值和阈值。该类方法由于梯度下降法是一种局部优化方法,最后所得的权值和阈值并非全局最优;② 将粒子群优化算法完全替换BP神经网络内置的最速梯度下降法,以期得到BP神经网络的最优权值和阈值。相比于第①类方法,第②类方法充分发挥了粒子群算法的全局寻优能力,可以以更小的误差搜索到最优权值和阈值。但是基本粒子群算法本身也存在不足,容易过早地收敛于局部最优解,此时的权值和阈值只是局部极小值点,并非全局最小值点。
鉴于此,该文在第②类方法的基础上做进一步改进,在基本粒子群算法中引入自然选择算子,按照自然选择机理,将粒子群体的目标函数值从小到大排序,并将前半部分粒子的位置和速度赋予后半部分粒子,对粒子群算法进行改进,用于BP神经网络权值和阈值的更新,搜索其最优解,从而形成基于自然选择PSO-BP神经网络算法,用于拟合自变量(黏聚力、内摩擦角)和因变量(稳定系数)的近似函数关系,构造功能函数,同时将上述神经网络算法和蒙特卡洛法相结合,求取可靠度指标β和失效概率Pf。最后以贵州省马达岭HP1滑坡为例,验证上述理论和方法的有效性。
2 BP神经网络的改进策略
2.1 BP神经网络基本原理
BP神经网络是一种信号向前传播、误差反向传播的多层前馈神经网络。基本的BP神经网络有3层,即输入层、输出层和隐含层,其拓扑结构如图1所示。
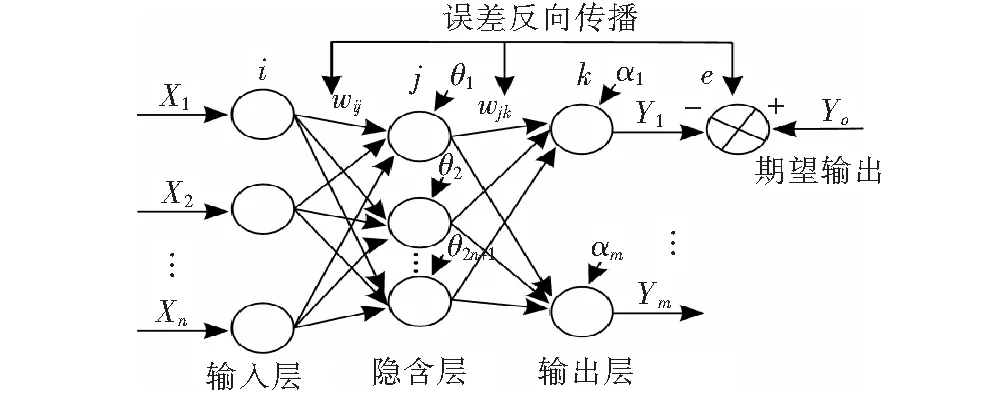
图1 3层BP神经网络拓扑结构
图中:2n+1为隐含层的节点数;wij(i=1,2,…,n;j=1,2,…,2n+1)为输入层到隐含层的连接权值;wjk(j=1,2,…,2n+1;k=1,2,…,m)为隐含层到输出层的连接权值;θj为隐含层的阈值;αk为输出层的阈值;X=[X1,X2,…,Xn]T为输入变量组成的向量;Y=[Y1,Y2,…,Ym]T为输出向量;e为预测输出与期望输出的误差。
传统的BP神经网络基于最速梯度下降法来调整网络的权值和阈值,使得网络的预测输出不断地逼近期望输出,误差最小。
2.2 采用更高阶方法调整权值和阈值的可行性
由于BP神经网络对其权值和阈值的初始设置较为敏感,并且可能因为初始参数设置的随机性而造成误差较大。本质上BP神经网络权值和阈值的调整是一个最优化问题,可表示为:
(1)
式中:
w=[w11,w12,…,wij,w11,w12,…,wjk]Tw⊂R
(2)
θ=[θ1,θ2,…,θ2n+1]Tθ⊂R
(3)
α=[α1,α2,…,αm]Tα⊂R
(4)
(5)

虽然BP神经网络内置的最速梯度下降法也是一种通用的非线性优化方法,然而当前在非线性优化方法领域,一系列智能算法显示出更好的全局寻优性能。因此,基于模块化的理论,采用更高阶的优化方法来替换传统BP神经网络内置的最速梯度下降法,进行算法升级,以期获得更佳的性能,这是一个可行的方案。
3 采用自然选择策略的粒子群算法优化BP神经网络的权值和阈值
3.1 粒子群算法基本原理
对形如式(1)的优化问题,其以BP神经网络的权值和阈值为自变量,以BP神经网络的预测输出和期望输出的误差平方和为目标函数,通过寻找BP神经网络权值和阈值的最优组合,使目标函数达到最小。鉴于粒子群算法具有很好的全局搜索能力,该文选用粒子群算法寻优。在D维搜索空间中,假定粒子i的位置为Xi=(xi1,xi2,…,xiD),速度Vi=(vi1,vi2,…,viD),通过粒子个体最优位置pbest和粒子群体最优位置gbest的比较,粒子i更新自己的位置和速度:
Vi,j(t+1)=w×Vi,j(t)+c1r1[pbest-Xi,j(t)]+c2r2[gbest-Xi,j(t)]
(6)
Xi,j(t+1)=Xi,j(t)+Vi,j(t+1)
(7)
w=wmax-(t-1)(wmax-wmin)×(maxgen-1)
(8)
式中:w为惯性权重,wmax=0.9,wmin=0.4;t为当前迭代次数;maxgen为最大迭代次数;c1,c2为学习因子,c1=c2=2;r1,r2为[0, 1]之间的随机数。
3.2 基于自然选择策略的算法改进
基本粒子群算法在寻优过程中如若搜索到一个局部最优解,则剩余所有粒子往往向其靠拢,出现过早收敛局部最优的情况。借鉴遗传算法中的选择思想,在基本粒子群算法之上引入自然选择算子,按照自然选择机理,在每次迭代寻优过程中,将粒子群体的目标函数值从小到大排序,并将其中前半部分粒子对应的位置和速度赋予后半部分粒子,且每个粒子保留以往的最优函数值,这样即可增加粒子群体中靠近最优解粒子所占的百分比,使每次迭代的粒子都具有较好的性能,提高收敛速度,从而形成基于自然选择策略的混合粒子群算法。对于当前迭代次数t,将所有粒子的目标函数值排序:
[a,b]=sort(G)
(9)
Index=round[(N-1)/2]
(10)
X{b[(N-Index+1):N]}=X[b(1:N)]
(11)
V{b[(N-Index+1):N]}=V[b(1:N)]
(12)
式中:sort为升序排列函数;N为粒子的个数。
3.3 自然选择粒子群算法优化权值和阈值
采用自然选择粒子群算法对式(1)的优化目标函数进行优化。将BP神经网络的权值和阈值作为待优化的变量,其构成的向量表示成粒子i的位置向量Xi=(xi1,xi2,…,xiD),D为BP神经网络权值和阈值的总个数,式(1)作为自然选择粒子群算法待优化的目标函数。对于n个训练样本(输入变量为黏聚力、内摩擦角,输出变量为稳定系数),在确定BP网络的拓扑结构后,可将粒子群算法产生的初始位置(权值和阈值)赋予BP神经网络,并依据训练样本数据,BP神经网络计算式(1)所示的目标函数,将该值返回给粒子群算法中的粒子,粒子通过目标函数值的比较,确定当前粒子群体中的全局最小值及最优位置,并判断是否达到最大迭代次数。若未达到最大迭代次数,粒子依据式(6)~(12),进行位置(权值和阈值)更新,并将其赋予BP神经网络的权值和阈值,继续计算式(1)的目标函数,返回给粒子。如此循环,直至达到最大迭代次数。将此时自然选择粒子群算法搜索到的最优权值和阈值赋予BP神经网络。
4 采用基于自然选择PSO-BP神经网络构造功能函数
滑坡可靠性分析的重点之一是提取功能函数g(X),这是从物理模型到数学模型概化的关键一步。假设可靠性分析中存在n个随机变量,稳定系数fos是n个随机变量x1,x2,…,xn的函数,令X=[x1,x2,…,xn]T,记为fos(X)。则功能函数可表示为g(X)=fos(X)-1。上述功能函数g(X)是隐式的,且具有显著的非线性。针对这一情况,该文采用自然选择PSO-BP神经网络构造功能函数。将可靠性分析的随机变量(如黏聚力、内摩擦角)作为输入变量,g(X)作为输出变量。基于均匀设计法取样,构造功能函数。
5 基于自然选择PSO-BP神经网络滑坡可靠性计算流程
采用自然选择PSO-BP神经网络构造功能函数,并和蒙特卡洛法(MCS)相结合,计算滑坡的可靠度指标β和失效概率Pf。基本步骤如下:
(1)数据预处理。确定滑坡可靠性分析随机变量(如黏聚力、内摩擦角)的个数,采用均匀设计法构造n个样本。基于此样本,采用SLOPE/W(稳定性计算方法为Morgenstern-Price法)计算n个样本的稳定系数fos,并将其数值减一。将上述样本作为训练样本,为消除各变量之间数据的量级影响,采用mapminmax函数统一进行标准化。
(2)初始化BP神经网络。确定BP网络的拓扑结构、神经元传递函数。该文采用n-2n+1-m的三层神经网络,则粒子的维度D采用下式计算:
D=n×(2n+1)+(2n+1)×m+(2n+1)+m
(13)
对于该BP神经网络,输入层至隐含层的传递函数选用logsig函数,隐含层至输出层的传递函数选用purelin函数。
(14)
purelin(x)=x
(15)
(3)确定粒子群的基本参数。包括粒子数N、迭代次数maxgen等,并同时初始化各粒子的飞行速度和位置(权值和阈值组成的向量)。
(4)将粒子初始位置赋予BP神经网络,并计算式(1)的目标函数,将其赋予粒子i,同时将粒子当前个体最优位置赋予pbest,整个粒子群当前最优位置赋值于gbest,全局最小目标函数值赋予fitnessbest。
(5)判断是否达到最大迭代次数。若满足,则将此时的权值和阈值赋予BP神经网络,执行步骤(9)~(10)。否则,执行步骤(6)~(8)。
(6)对于粒子i,依据式(6)、(7)更新其速度和位置。
(7)将粒子i新目标函数值和以往最小目标函数值相比较,若新目标函数值较小,则将其替换以往目标函数值,并将此时的最优位置替代pbest。同时,将新目标函数值和以往全局最小目标函数值fitnessbest相比较,若新目标函数值较小,则将其作为新的fitnessbest,并将此时的位置替换gbest。
(8)依据自然选择机理,将当前所有粒子的新目标函数值按从小到大排序,并将前半部分粒子对应的位置和速度赋予后半部分粒子,且每个粒子保留当前的最优函数值,并返回步骤(5)。
(9)据随机变量的分布形式,随机生成Q组数据用于测试BP神经网络,并计算期望输出与预测输出的绝对误差和,进行拟合精度分析。
(10)基于训练好的BP神经网络,依据随机变量的分布形式,生成M组随机变量,并将其运用于神经网络的输出计算,统计其中小于零的个数P。当M足够大时,依据式(16)、(17)计算失效概率Pf和β。
(16)
β=Φ-1(1-Pf)
(17)
式中:Φ为标准正态分布函数。
自然选择PSO-BP神经网络可靠度计算流程见图2。

图2 自然选择PSO-BP神经网络可靠度计算流程图
6 实例分析
为验证基于自然选择策略PSO-BP神经网络的全局拟合能力,采用贵州省马达岭HP1滑坡为例进行分析。基于自然选择PSO-BP神经网络构造功能函数,并结合蒙特卡洛法,计算该滑坡4种工况下的可靠性指标,而后对其稳定状态做出评价。
6.1 马达岭滑坡基本特征
马达岭滑坡位于贵州省都匀市南西方向,直线距离约24 km,地理坐标为东经107°17′48″,北纬26°11′01″。依据斜坡变形破坏特征,将斜坡区域分为已滑滑坡HP1、HP1滑坡堆积体经降雨搬运后的泥石流NSL1区域、滑坡隐患DY208-1三部分。
斜坡为一平缓反倾斜横向坡,上陡下缓。岩层近南北走向,缓倾向坡内,呈软硬互层结构。斜坡上覆第四纪残坡积土,陡崖下部分布有以砂岩、泥岩为主的崩坡积物,冲沟中为第四纪冲洪积层。基岩出露地层自上而下分别为细粒石英砂岩、炭质页岩和煤层,灰色中厚层状粗晶生物灰岩夹细粒石英砂岩,细晶灰岩和泥盆系上统高坡场组细晶白云岩。
马达岭滑坡位于都匀至香格里拉高速公路原有规划线上,且该滑坡前缘距离规划线路较近。由于滑坡主要物质成分为砂岩、页岩及煤层,结构松散,且由于煤层开采,在坡顶形成裂缝,变形严重,在极端降雨条件下滑坡可能失稳,对原有线路造成威胁。为此该文取HP1滑坡为可靠性分析对象,其地质剖面如图3所示。

6.2 马达岭滑坡岩土体物理力学参数
结合已有研究成果和现场调查,将岩土体参数进行一定折减,得马达岭滑坡HP1各个层位岩土体的物理力学参数值,见表1。

表1 HP1滑坡岩土体物理力学参数
对马达岭HP1滑坡地质剖面进行简化,不考虑裂缝的影响,选取表1各土层天然状态下的物理力学参数作为材料参数,采用SLOPE/W(计算方法为M-P法)进行计算,预置搜索的滑面为10 000条。经计算,得临界滑动面的位置(图4),滑面为近似圆弧形,据此滑面作可靠性分析。

图4 马达岭HP1滑坡临界滑动面计算结果
为考虑地震对HP1滑坡稳定性的影响,结合地震相关规范和现场调查,取地震动水平加速度为0.05g,相应的地震基本烈度为Ⅵ度,采用拟静力法对其进行分析。分别计算HP1滑坡在天然、天然+地震、饱和、饱和+地震4种工况下的可靠度指标β和失效概率Pf。
6.3 基于均匀设计法取样
将碎石土的黏聚力c值和内摩擦角φ值考虑为随机变量,且服从独立正态分布,其均值和变异系数采用表1的数据,而其余变量视为确定性变量。依据随机变量的取值区间[μ-3σ,μ+3σ]生成20组样本,并基于均匀设计法取样,而后将上述样本点采用SLOPE/W计算稳定性系数fos,计算方法为M-P法,假设土体的破坏服从Mohr-Coulomb准则,同时将其数值减1,得20组训练样本,如表2所示。
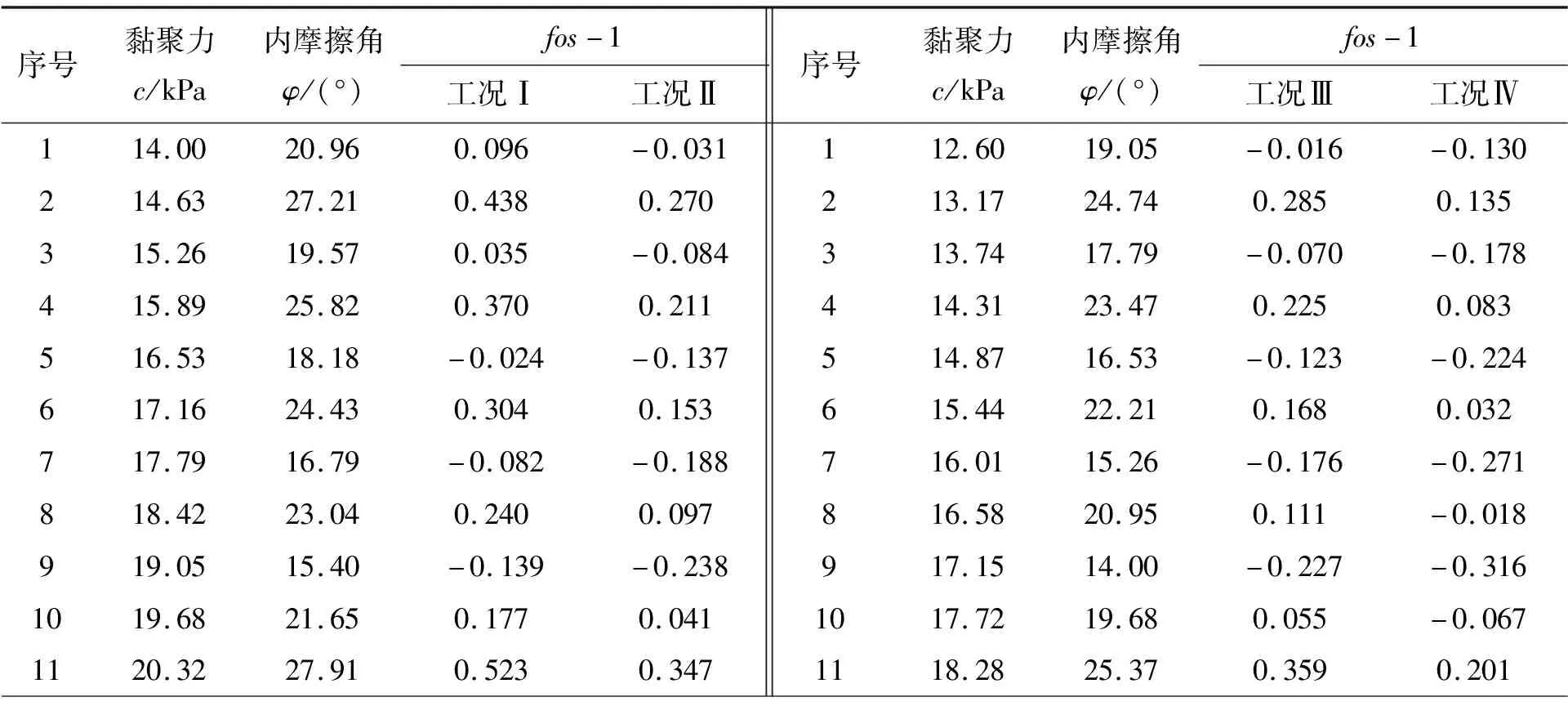
表2 均匀设计样本

续表2
注:Ⅰ、Ⅱ、Ⅲ、Ⅳ分别代表天然工况、天然+地震工况、饱和工况、饱和+地震工况。
6.4 误差分析
为分析PSO-BP神经网络在引入自然选择算子后的有效性,需对BP神经网络和PSO算法参数进行设置:
(1)BP神经网络:网络的拓扑结构为2-5-1;训练函数为traingd;学习函数为learngd;学习率为0.01;输入层至隐含层的传递函数为logsig,隐含层至输出层的传递函数为purelin。
(2)PSO算法:粒子数N=30;粒子的飞行速度区间范围为[-1,1],当其飞行速度超过该区间的上下限时,分别将上下限赋予该粒子;初始化权值和阈值的区间范围为[-5,5];天然、天然+地震、饱和、饱和+地震工况下的最大迭代次数maxgen分别为2 000、2 600、3 600、3 300。
基于上述基本参数,采用生成的均匀设计样本点分别对传统BP神经网络、PSO-BP神经网络和基于自然选择策略的PSO-BP神经网络进行训练,并依据变量的分布形式随机生成15组样本用于测试网络,经计算,得到3种网络的训练误差曲线及误差如图5~8及表3所示。

图5 天然工况下训练误差

图6 天然+地震工况下训练误差

图7 饱和工况下训练误差

图8 饱和+地震工况下训练误差

表3 网络误差结果
6.5 HP1滑坡可靠性分析
基于上述训练好的BP神经网络,依据变量的分布形式随机生成100万组数据作为输入变量,并驱动上述训练好的BP神经网络,计算相应的输出(fos-1),同时据式(16)、(17)计算Pf和β。为检验上述BP神经网络的精度,以直接蒙特卡洛法(MCS)抽样100万次的计算结果为基准,稳定性计算方法为M-P法。4种方法计算结果如表4所示。

表4 可靠度指标计算结果
7 结果分析
7.1 神经网络预测误差分析
由图5~8、表4可知:① 相对于传统BP神经网络,PSO-BP神经网络和基于自然选择策略的PSO-BP神经网络的训练误差和预测绝对误差和都比其要小。就训练误差而言,它们相差两个量级,可见基于最速梯度下降法搜索最优权值和阈值能力有限,容易收敛局部最优,而基于智能算法(PSO)优化权值和阈值,能够收敛于更优的权值和阈值,使得训练误差更小。就预测误差而言,饱和工况下,传统BP神经网络的预测绝对误差和为1.247,而PSO-BP神经网络和自然选择PSO-BP神经网络的误差分别为0.045、0.041,可见采用智能算法(PSO)优化的BP神经网络预测结果更为精确,误差更小;② 基于自然选择PSO-BP神经网络其4种工况下的训练误差和预测绝对误差和比PSO-BP神经网络都要小,其中饱和+地震工况下的训练误差和预测绝对误差和最小,PSO-BP神经网络、自然选择PSO-BP神经网络的训练误差分别为1.27×10-4、1.14×10-4,而预测绝对误差和仅为0.040、0.038。可见自然选择算子的引入,能够防止基本粒子群算法过早收敛于局部最优,从而达到全局最优,使改进后的网络有更好的全局拟合能力。
7.2 可靠性精度分析
由表4可知:基于自然选择PSO-BP神经网络和PSO-BP神经网络计算的可靠度指标与直接Monte Carlo法的绝对误差都比传统的BP神经网络要小,其中基于自然选择PSO-BP神经网络和Monte Carlo法相结合计算得到的可靠度指标与直接Monte Carlo法计算结果非常接近,β的最大绝对误差仅为0.043,失效概率最大误差仅为1.42%。可见,基于自然选择PSO-BP神经网络和蒙特卡洛法相结合的方法具有较好的计算精度,可以得到较小误差的可靠度指标。而相对于PSO-BP神经网络的计算结果,基于自然选择PSO-BP神经网络计算结果误差都比其要小。此外,针对该案例4种工况下的计算结果,基于自然选择PSO-BP神经网络与PSO-BP神经网络的结果相差并不是太大,这或许是随机变量个数较少的原因,当变量个数逐渐增加时,其权值和阈值的个数必然增加,从而优化问题也将变得复杂,基于自然选择PSO-BP神经网络的优越性势必也将凸显,这是今后进一步研究的方向。
7.3 影响因素敏感性分析
由表4可知:对比天然+地震、饱和两种工况下的可靠性计算结果,饱和工况下的可靠度指标β明显大于天然+地震工况下的计算结果,且该值和天然工况下的计算结果相对接近,故降雨对该滑坡可靠性的影响较小,敏感性低,而地震的影响较大,敏感性更高。
7.4 马达岭滑坡对公路线路的影响
鉴于马达岭滑坡前缘距离原规划路线较近,而HP1滑坡饱和+地震工况下的失效概率为71.04%,依据表5,可知其处于高危险状态,将对原有线路构成威胁。为减小滑坡对线路的影响,在后期施工图设计阶段,选取了防御绕避的措施,在滑坡影响区以南2 km修筑隧道穿过滑坡可能影响的范围。

表5 边坡稳定性等级
8 结论
(1)对于极限状态方程为隐式情况,采用BP神经网络对其进行拟合,由传统的BP神经网络容易陷入局部最优,采用基于自然选择PSO算法优化BP神经网络的权值和阈值,而后进行回归预测,结果表明基于自然选择PSO-BP神经网络具有更高的拟合精度,误差更小,能够应用于边坡可靠性分析。同时,改进后的网络期待在更加复杂案例中的运用。
(2)对于该滑坡可靠性计算结果可知,降雨对可靠性的影响要小于地震。
(3)据边坡稳定性等级划分,可知天然工况下的HP1滑坡处于稳定状态,饱和、天然地震工况下处于低危险状态,而饱和地震工况下处于高危险状态,所得结果有一定参考性。

