强降雨条件下弃土场边坡稳定性历程分析

抗兴培，孟凡成，曾超，王彪龙，郭将，刘晓*

(1.中国地质大学(武汉)教育部长江三峡库区地质灾害研究中心，湖北 武汉 430074；2.贵州高速公路集团有限公司；3.中交第二公路勘察设计研究院有限公司)

1 引言

弃土场是工程建设中常见的人工弃渣堆积体，在降雨、地震等工况下，极易发生滑坡、泥石流等自然灾害，如2015年的深圳红坳弃土场滑坡，给当地群众造成严重灾难。目前，国内外学者对降雨入渗条件下边坡稳定性的研究，主要集中在天然边坡方面，而对弃土场边坡稳定性的研究较少，对不同降雨条件下，降雨入渗速率的研究几乎没有。天然边坡多为非饱和边坡，在降雨入渗条件下，逐渐向饱和状态过渡，对应的斜坡稳定性发生瞬态改变。张社荣等、戚国庆、张亚国、潘思渝、王叶娇等、张玉等研究了在降雨条件下非饱和天然边坡内部渗流场变化，藉此分析该类边坡的稳定性；Li认为降雨在地层界面处汇聚，软化了接触面，随着降雨的持续，软化范围扩大，逐渐使其流态化，最终诱发滑坡；Bai通过对武都县某滑坡的研究，认为滑坡的发生与降雨强度有很大关系，当日降雨量超过20 mm，则极可能诱发黄土滑坡；Iverson等研究了降雨入渗对于滑坡灾害的促进作用，得到在黄土区降雨入渗深度一般限制在地下5 m以内；汪洋等研究了小降雨入渗下边坡稳定性的计算方法；蒋中明等分析了降雨入渗作用下三维边坡的渗流变化；Lei等研究了降雨入渗过程中细颗粒的迁移、沉积对边坡稳定性的影响。较之于天然边坡，弃土场边坡往往坡度较大、结构松散、密实性差，上层弃渣和下层第四系岩土在强度、渗透性等性质上有较大差别，这就导致其与天然边坡在降雨入渗条件下的内部渗流场、稳定性有较大差别。目前，高速公路建设过程中边坡稳定性的分析多集中在路堤边坡，如朱志勤等分析了降雨条件下公路路基边坡的渗流特性，对弃土场边坡在降雨条件下稳定性的研究较少。弃土场边坡的研究，多为矿山弃土场、城市弃土场，而对山区高速公路建设过程中形成的弃土场边坡，鲜有研究。金福喜等利用Abaqus有限元软件分析了某城市弃土场斜坡在不同类型降雨条件下的稳定性；吴志斌等模拟了不同降雨强度下城市弃土场边坡的内部渗流和稳定性。但是目前的弃土场边坡稳定性研究主要是取降雨过程中的某一时刻点或降雨进行中的某几个点来研究弃土场内部渗流和稳定性，显然忽略了非饱和弃土场边坡在降雨入渗整个过程中，其内部渗流场和边坡稳定性是一个随时间动态变化的过程。

该文以贵州山区平罗高速公路某弃土场边坡为例，在野外勘察、室内试验的基础上，用数值模拟方法对比分析降雨前-降雨中-降雨后的整个降雨入渗过程中，不同降雨强度条件下，降雨入渗速率、边坡内部渗流场和稳定性系数的变化规律。这对揭示山区高速公路弃土场滑坡灾害形成机理和指导该类灾害的防治具有一定的理论和现实意义。

2 工程概况

2.1 弃土场基本特征

贵州山区平(塘)罗(甸)高速公路某弃土场边坡，由岩质边坡开挖堆积而成，弃渣为白云质灰岩，夹黏土，原地形为倾角约22°的斜坡。该弃土场占地面积4.3×103m2，平均厚度约15 m，弃渣量约6万m3，坡面走向SE105°。原河道因弃土场堵塞而改道上移，河道下游约1 km为董当乡政府所在地，弃土场边坡的失稳对其构成严重威胁。利用SLOPE/W建立分析模型(图1)，根据实地勘察，弃土场边坡模型背坡侧地下水位为520 m，坡脚侧地下水位488 m。

2.2 岩土体物理力学指标确定

根据现场调查，结合部分室内试验和前人在贵州山区弃土场的研究成果，得到岩土物理力学参数如表1所示。

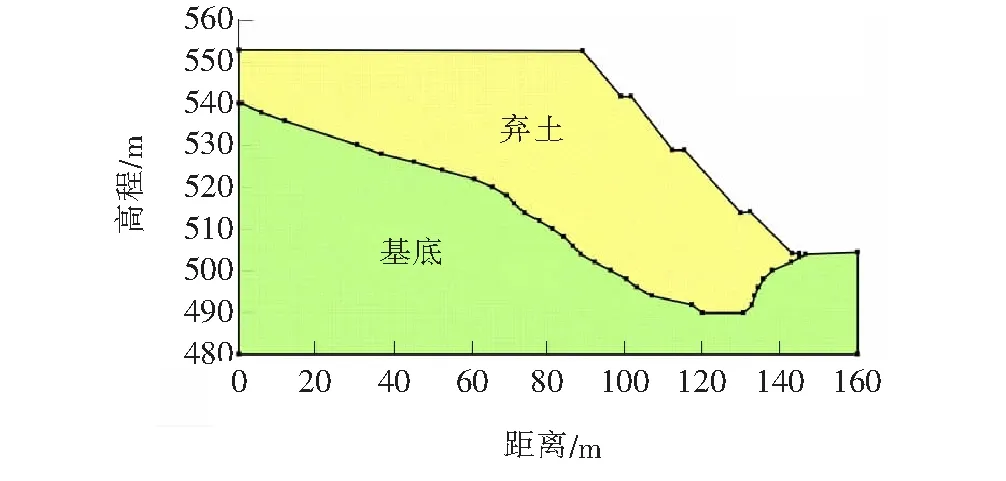
图1 弃土场边坡模型

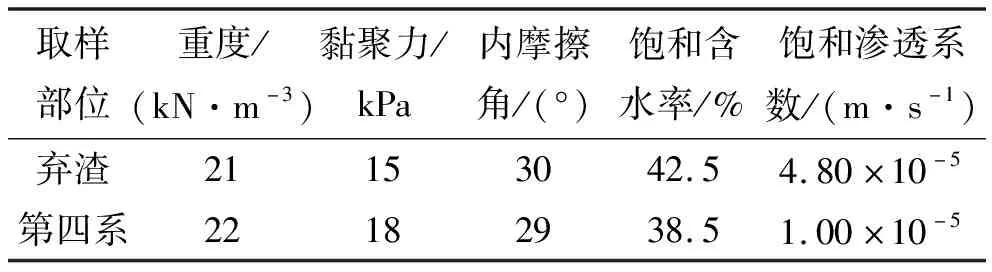
表1 弃土场岩土体物理力学指标

3 降雨入渗条件下坡体饱和-非饱和渗流分析

3.1 饱和-非饱和渗流基本理论

边坡的地下水位线一般为饱和区与非饱和区的分界线，随着降雨的进行，边坡体内的饱和区与非饱和区的范围随之变化。Richards借助对流体通过多空隙介质中毛细管传导作用的研究提出：达西定理仍然可以用来描述非饱和土中水的运动，但此时渗透系数不再为常数，而是与体积含水量有关的常数。当非饱和土的体积含水量减小时，空气填充的空隙增加，使得过水面积减小，渗流流径弯曲度增加，致使渗透系数减小。基于质量守恒原理及达西定律，在等热条件下，多维各向异性的非饱和区水分运动的基本方程为：

(1)

式中：h为水头；kx、ky、kz为x、y、z方向的渗透系数；θ为含水量；C(θ)为比水容重，物理意义为压力变化所引起土中含水量的变化：

(2)

式中：α、m、n为拟合参数；θs为饱和体积含水量；θr为剩余体积含水量(通常认为是饱和体积含水量的10%)；Se为相对饱和度，Van-Genuchen(1980，VG模型)拟合的水土特征曲线方程(SWCC)即：

(3)

其中：ψ为基质吸力[假设n=1/(1-m)，且n>1]。

VG模型是目前国内外最为普遍的描述土壤水分特征曲线的方法，其中：

(4)

(5)

结合表1数据，由式(5)得到上层弃土和下层第四系岩土土水特征曲线如图2所示。

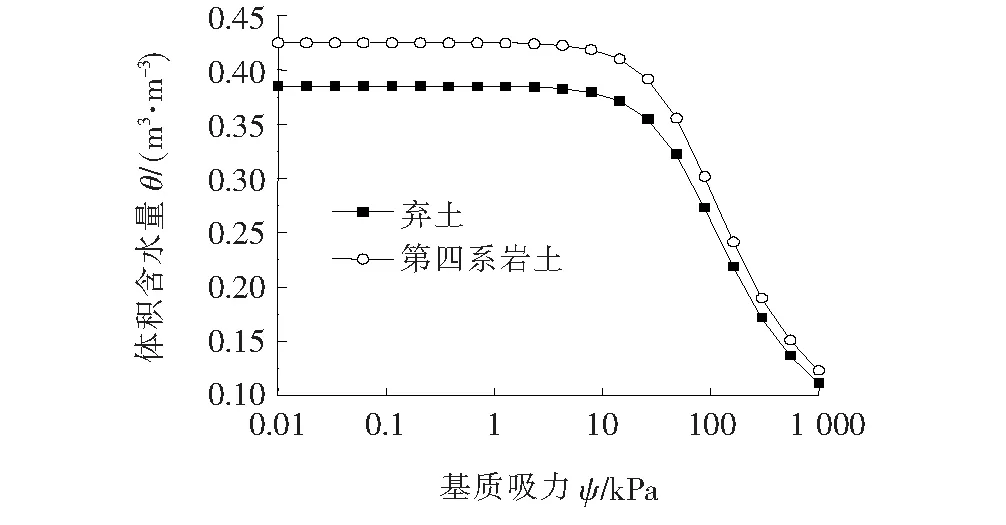
图2 土水特征曲线

由式(4)得到上层弃土和下层第四系岩土渗透函数随基质吸力的变化曲线如图3所示。

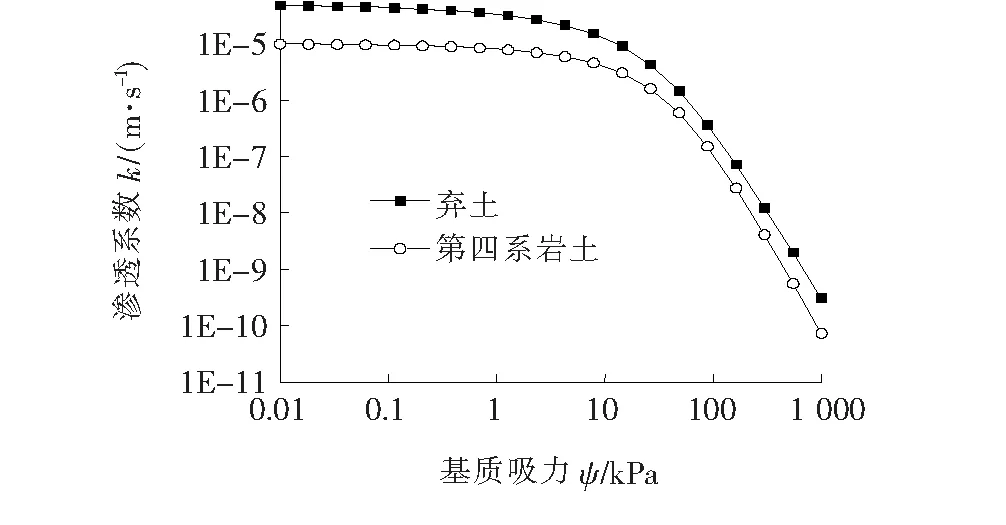
图3 土体渗透系数

3.2 定水头边界条件

在弃土场边坡模型背坡侧和坡脚侧分别施加地下水位为520 m和488 m的定水头边界。即：

(6)

式中：r1为水头边界。

3.3 降雨入渗边界条件

一般认为，降雨强度和坡体表层的渗透系数是制约降雨入渗过程的直接控制因素，而坡体深层的渗透系数又基于渗流连续性原理间接影响到表层坡体雨水的下渗过程，因此降雨入渗速率是坡体渗透系数和降雨强度这两个控制因素作用下的结果，这3个物理量的量纲均为m/s。现对降雨强度不变情况下的降雨入渗过程，及其对应的边界条件予以阐述。

根据表1和图3，在降雨初期，降雨强度远高于土体表层的非饱和渗透系数，此时的降雨入渗速度大大低于降雨强度，在坡体表面迅速产生地表径流，形成水膜，称之为“积水模型”，在不考虑积水深度的情况下，以坡表高度为水头，按式(6)设置边界条件。

随着降雨入渗过程的推进，坡表土体的含水量逐渐升高直至达到饱和，其渗透系数随之升高至饱和渗透系数。此时又分为两种情况：

(1)表层土体饱和渗透系数大于降雨强度。在初期的定水头边界条件下，随着降雨入渗过程的推进，降雨入渗速率逐步提高直至逼近降雨强度，而降雨强度决定了入渗速率的上限，因此，此时边界条件切换为流量边界，如式(7)所示：

(7)

式中：r2为流量边界。

(2)表层土体饱和渗透系数小于降雨强度。在初期的定水头边界条件下，随着降雨入渗过程的推进，尽管坡表土体渗透性不断提高直至达到饱和，但仍然不足以接纳全部降雨，因此地表仍然存在弃水，边界条件仍为定水头边界。

SEEP/W内置了上述降雨入渗过程带来的边界条件转换算法，因此能够方便地进行饱和-非饱和渗流分析。即在降雨条件下,非饱和坡表为水头边界,随着降雨入渗至饱和时,饱和坡表为流量边界。

贵州山区多强降雨，该文以该地区1961—2012年的50年平均最大日降雨量、50年一遇最大日降雨量、100年一遇最大日降雨量为降雨条件，假设降雨为等强降雨，降雨持时24 h,降雨强度及对应的降雨速率见表2。以弃土场边坡地表为迎水断面，其长度为183.7 m，宽度为单位宽度，假设未入渗雨水以地表径流形式迅速流失，而不在坡体表面形成水头。

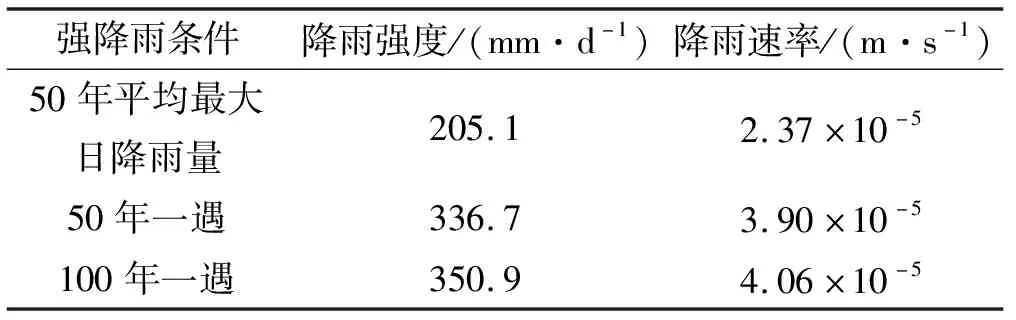
表2 弃土场所在地区降雨强度

采用SEEP/W有限元软件分析弃土场边坡在3个不同降雨强度下，分别在降雨前、降雨过程中、降雨结束时、降雨结束后的内部渗流场变化情况。图4(a)～(g)展示了日降雨量205.1 mm时的渗流场，其中虚线为孔隙水压力为零的等势面，实线为土层分界面。

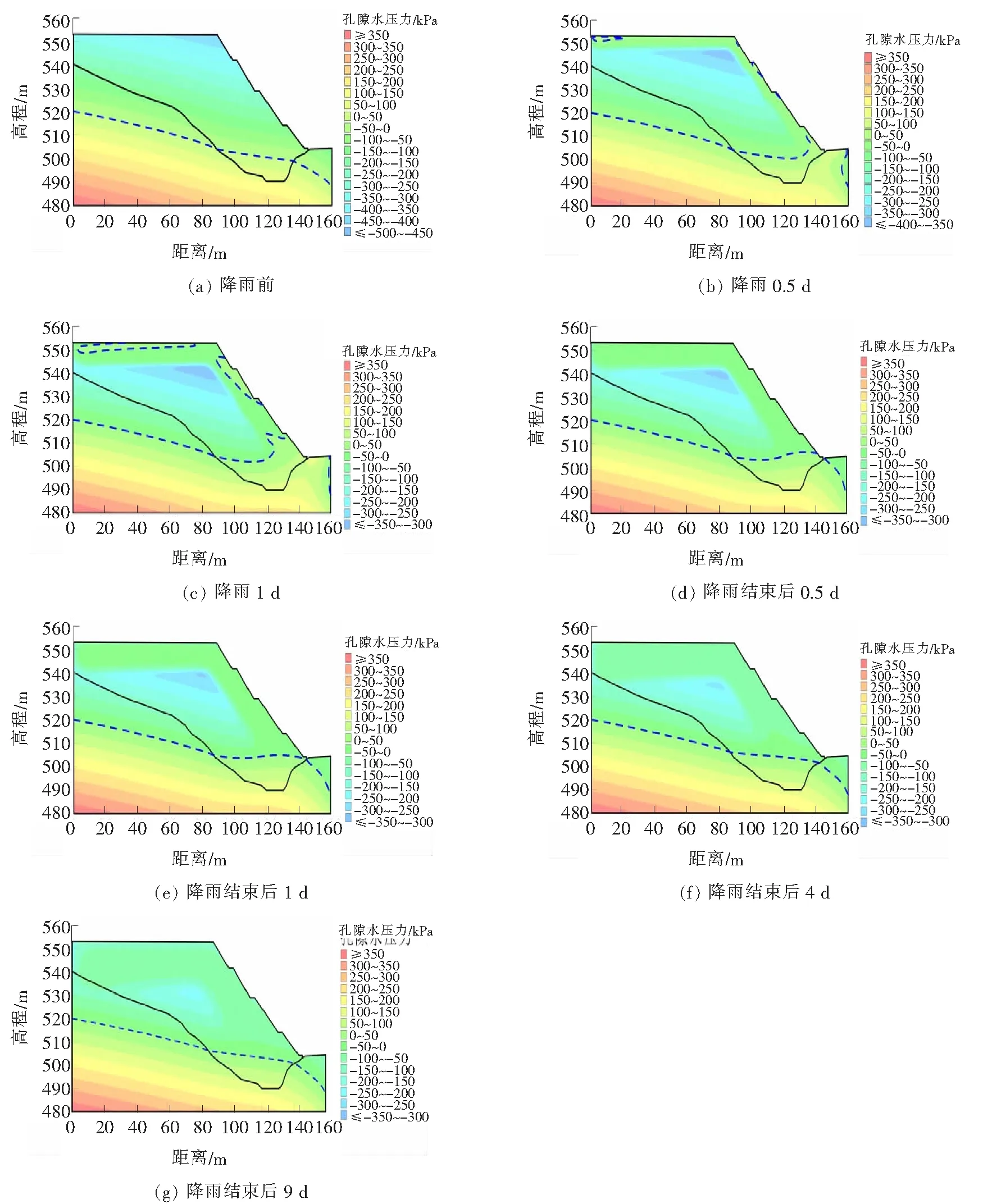
图4 不同时间的渗流场(日降雨量205.1 mm)

由图4可知：

(1)弃土场边坡在天然状态下，因上层弃渣较之于下层第四系岩土，其密实性更差，渗透系数更大。由于渗流总是倾向于寻找阻力小的路径，使得地下水位线穿过弃渣体时出现向上凸起现象。

(2)暴雨过程中，弃土场边坡内部渗流发生显著变化，其表面迅速饱和，出现短暂的潜水位，随着降雨的进行，出现地表径流。

(3)降雨结束后，弃土场表面饱和区域恢复不饱和状态，弃土场边坡内部存在一个低孔隙水压力区域。对比图4(a)与图4(g)，除了地下水位面有细微差别，明显差别在于其上的低孔隙水压力分布区的变化。说明降雨结束后，系统逼近但并不能完全恢复到降雨前的初始状态，而此次降雨后的稳定态又将成为下一次降雨的初始态，如此周而复始，形式上在往复，实质上在发展，这也从岩土力学这一侧面，验证了普利高津耗散结构的不可逆理论。

4 不同降雨条件下入渗速率分析

以该地区50年平均最大日降雨量、50年一遇最大日降雨量、100年一遇最大日降雨量为强降雨条件，对比分析不同降雨强度条件下，整个降雨过程中，降雨入渗速率的变化规律(图5)。

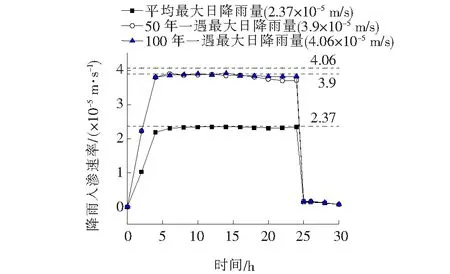
图5 降雨入渗速率曲线

由图5可知：

(1)随着强降雨的进行，降雨入渗速率先迅速增加，然后趋于稳定值，接近于降雨强度。最大的降雨入渗速率，出现在降雨进行约6 h时。结合边坡内部渗流场分析认为：降雨前期阶段，降雨强度大于坡表土体的渗透系数，降雨入渗速率主要受土体渗透系数制约，随着强降雨的进行，坡体表面区域由非饱和状态逐渐转为饱和态，坡表土体的渗透系数逐渐增大至最大值，其大小高于降雨强度，此时降雨强度为制约降雨入渗的主要条件。

(2)随着降雨强度的增加，最大降雨入渗速率随之增大，其所需时间也越短。

5 不同强度降雨条件下边坡稳定性分析

Mohr-Coulomb方程的修正形式常被用来描述非饱和土的抗剪强度，即：

s=c′+(σn-σa)tanφ′+(μa-μw)tanφb

(8)

式中：s为抗剪强度；c′为有效黏聚力；φ′为有效内摩擦角；φb为定义角，即剪力强度随基质吸力增加。

Vanapalli等根据非饱和土的土-水特征曲线和饱和土的抗剪强度参数，建立了预测非饱和土体剪切强度的经验分析模型，找到了较好的φb替代，即：

(9)

式中：θw为体积含水量；θr为残余体积含水量，常假定为饱和体积含水率的10%。

基于上述理论，以该地区1961—2012年的平均最大日降雨量、50年一遇最大日降雨量、100年一遇最大日降雨量为降雨条件，结合降雨条件下边坡内部渗流场变化，利用SLOPE/W数值模拟软件基于Morgenstern-Prince极限平衡法得到不同时刻边坡最危险滑面，以日降雨量205.1 mm为例分析不同降雨强度条件下边坡稳定性系数fos在整个降雨过程中的变化规律(图6)。

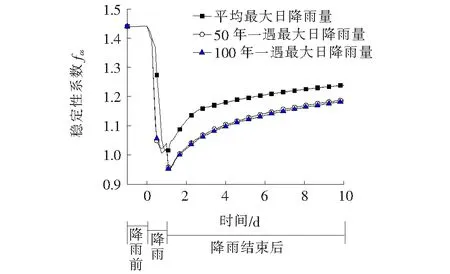
图6 边坡稳定系数

由图6可知：

(1)边坡稳定性系数总体变化趋势为：随着降雨的进行迅速减小，在降雨停止后一段时间，继续下降到达最小值后缓慢增加，最后趋于平稳。整个过程中弃土场边坡的最小稳定性系数并非出现在降雨过程中，而是降雨结束后的2～6 h之间。结合渗流场变化规律，分析认为：降雨结束后的一段时间内，弃土场边坡表面区域由饱和向非饱和状态转变，产生朝向坡面的渗透力，从而增加了坡体的下滑力，使得斜坡稳定性系数减小。

(2)随着降雨强度的增加，弃土场边坡最低稳定性系数随之减小。值得注意的是：50年一遇和100年一遇的强降雨条件下，二者的稳定性系数大小基本相同，随时间变化的趋势基本一致，在降雨18 h至降雨结束时间段内，其稳定性系数出现小幅增加。结合弃土场边坡渗流分析认为：暴雨到达一定的强度时，制约降雨入渗速率的主要因素转变为坡体岩土渗透系数，不再是降雨强度。特大暴雨持续一段时间后，在坡体表面形成较厚的饱和区域，其孔隙水压力大于坡体内部的非饱和区域，致使产生朝向坡内的渗透力，从而使坡体的抗滑力和作用在坡体的正压力增加，使得边坡稳定性系数增加。

6 结论

以贵州山区平罗高速公路某弃土场边坡详勘为基础，结合室内试验和已有资料，通过Geo-Studio数值模拟软件分析了整个降雨过程中，非饱和弃土场边坡在不同强度降雨条件下，内部渗流场、降雨入渗速率和边坡稳定性的变化规律，得出如下结论：

(1)强降雨过程中弃土场边坡表面区域迅速饱和，出现短暂的潜水位，在弃土场边坡内部形成有低孔隙水压力区。

(2)强降雨的初始阶段，坡表土体的渗透系数为制约降雨入渗速率的主导因素，随着坡表土体饱和度的增加，降雨强度逐渐转变为制约降雨入渗速率的主要因素。降雨强度的增加使得降雨入渗速率最大值也随之增加并使达到最大入渗速率的时间缩短。

(3)整个降雨过程中，弃土场边坡稳定性系数先急剧减小，后缓慢增加，由于降雨结束后坡体表面饱和区域产生指向坡面的渗透力，使得边坡稳定性系数在降雨结束后继续减小一段时间，之后的2～6 h时间段出现最小值。

(4)当暴雨强度到达一定值时，受降雨入渗速率制约，斜坡稳定性系数变化规律不再随降雨强度的增加而产生较大改变，降雨过程中由于边坡表面饱和区域产生指向坡体内部低孔隙水压力区的渗透力，使得随着强降雨的进行，边坡稳定性系数反而增加。