夯实基础，学好直线

伏建彬

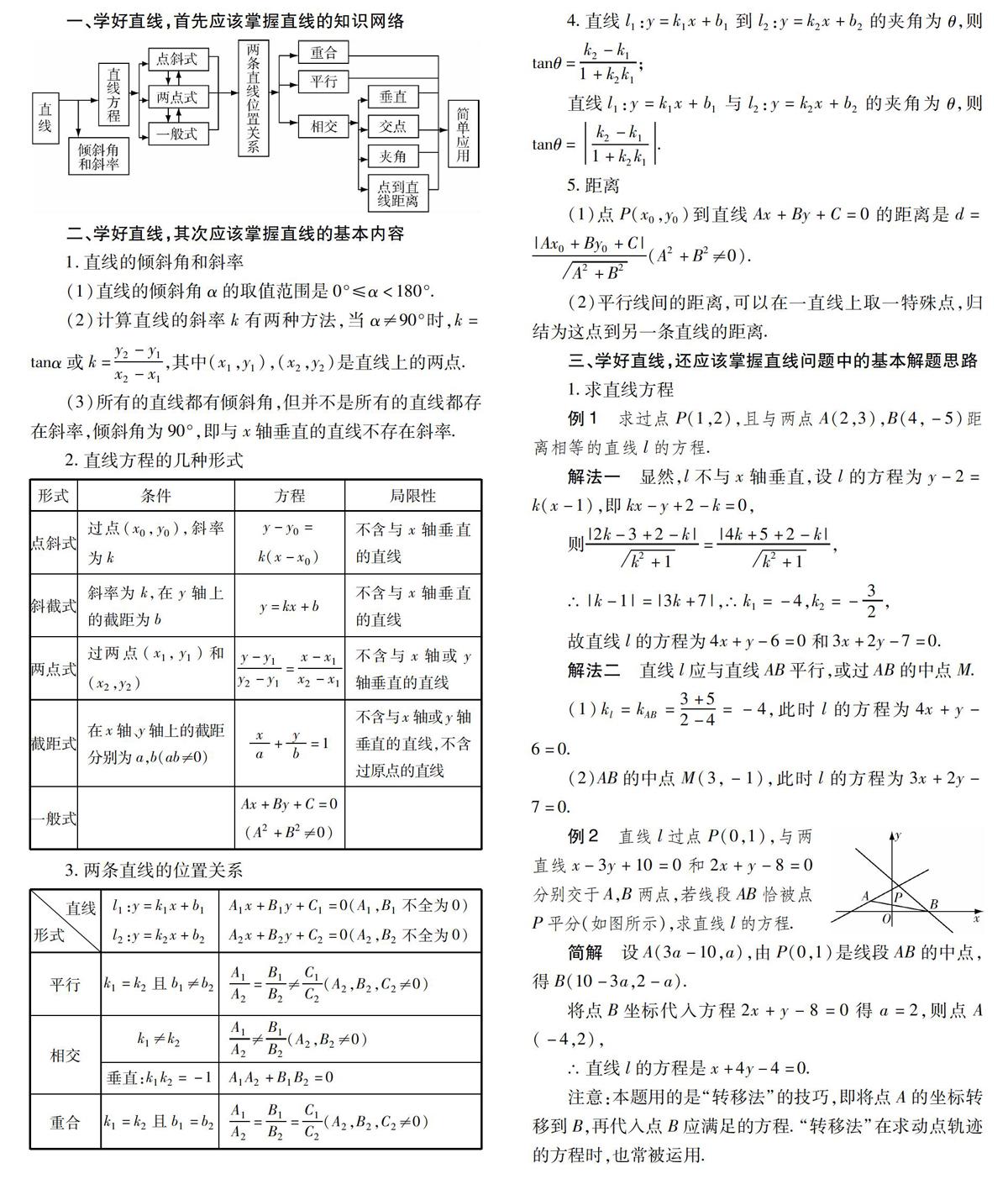
一、学好直线，首先应该掌握直线的知识网络

二、学好直线，其次应该掌握直线的基本内容

1.直线的倾斜角和斜率

（1）直线的倾斜角α的取值范围是0°≤α<180°.

（2）计算直线的斜率k有两种方法，当α≠90°时，k=tanα或k= y2-y1 x2-x1 ，其中（x1，y1），（x2，y2）是直线上的两点.

（3）所有的直线都有倾斜角，但并不是所有的直线都存在斜率，倾斜角为90°，即与x轴垂直的直线不存在斜率.

2.直线方程的几种形式

形式  条件 方程  局限性

点斜式 过点（x0，y0），斜率为k y-y0=k（x-x0） 不含与x轴垂直的直线

斜截式 斜率为k，在y轴上的截距为b y=kx+b 不含与x轴垂直的直线

两点式 过两点（x1，y1）和（x2，y2）  y-y1 y2-y1 = x-x1 x2-x1  不含与x轴或y轴垂直的直线

截距式  在x轴、y轴上的截距分别为a，b（ab≠0）   x a + y b =1  不含与x轴或y轴垂直的直线，不含过原点的直线

一般式  Ax+By+C=0（A2+B2≠0）

3.两条直线的位置关系

直线形式   l1：y=k1x+b1l2：y=k2x+b2

A1x+B1y+C1=0（A1，B1不全为0）

A2x+B2y+C2=0（A2，B2不全为0）

平行 k1=k2且b1≠b2  A1 A2 = B1 B2 ≠ C1 C2 （A2，B2，C2≠0）

相交

k1≠k2  A1 A2 ≠ B1 B2 （A2，B2≠0）

垂直：k1k2=-1 A1A2+B1B2=0

重合 k1=k2且b1=b2  A1 A2 = B1 B2 = C1 C2 （A2，B2，C2≠0）

4.直线l1：y=k1x+b1到l2：y=k2x+b2的夹角为θ，则tanθ= k2-k1 1+k2k1 ;

直线l1：y=k1x+b1与l2：y=k2x+b2的夹角为θ，则tanθ=  k2-k1 1+k2k1  .

5.距离

（1）点P（x0，y0）到直线Ax+By+C=0的距离是d= |Ax0+By0+C|  A2+B2  （A2+B2≠0）.

（2）平行线间的距离，可以在一直线上取一特殊点，归结为这点到另一条直线的距离.

三、学好直线，还应该掌握直线问题中的基本解题思路

1.求直线方程

例1   求过点P（1，2），且与两点A（2，3），B（4，-5）距离相等的直线l的方程.

解法一  显然，l不与x轴垂直，设l的方程为y-2=k（x-1），即kx-y+2-k=0，

则 |2k-3+2-k|  k2+1  = |4k+5+2-k|  k2+1  ，

∴|k-1|=|3k+7|，∴k1=-4，k2=- 3 2 ，

故直線l的方程为4x+y-6=0和3x+2y-7=0.

解法二  直线l应与直线AB平行，或过AB的中点M.

（1）kl=kAB= 3+5 2-4 =-4，此时l的方程为4x+y-6=0.

（2）AB的中点M（3，-1），此时l的方程为3x+2y-7=0.

例2   直线l过点P（0，1），与两直线x-3y+10=0和2x+y-8=0 分别交于A，B两点，若线段AB恰被点P平分（如图所示），求直线l的方程.

简解  设A（3a-10，a），由P（0，1）是线段AB的中点，得B（10-3a，2-a）.

将点B坐标代入方程2x+y-8=0得a=2，则点A（-4，2），

∴直线l的方程是x+4y-4=0.

注意：本题用的是“转移法”的技巧，即将点A的坐标转移到B，再代入点B应满足的方程.“转移法”在求动点轨迹的方程时，也常被运用.