活跃在不等式试题中的几个重要不等式

安徽省枞阳县宏实中学(246700) 江保兵

在中学数学期刊杂志中如《数学通报》、《数学通讯》、《数学教学》等等每期都推出几道的不等式试题, 不等式问题专家安振平先生每天在新浪博客中都推出几道新颖的不等式试题,这些精美的不等式,往往使人绞尽脑汁,但又让人爱不释手.在敬佩、感叹之余,人们心中往往产生一个疑惑: 这些不等式是怎么想到的? 可有什么命制试题的方法?笔者发现,无论是期刊上的征解试题,还是安振平先生博客中的不等式试题,有几个重要的不等式在试题命制时使用的频率较高,因此我们非常有必要对这些不等式有所了解.

1.琴生不等式

琴生不等式是丹麦数学家琴生在1905年至1906年间所建立的,具体内容如下:

若函数f(x) 为区间I 上的凸函数, 则对任意xi∈I,λi>0(i=1,2,··· ,n),且λ1+λ2+···+λn=1,则有:

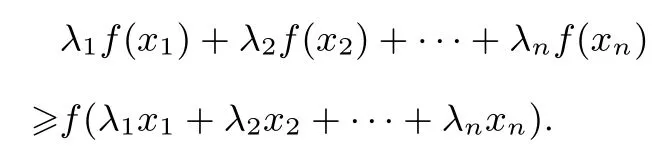
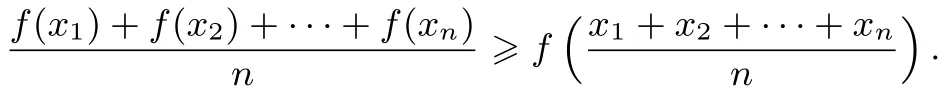
若函数f(x)为区间I 上的凹函数,上述不等式反向.

例1(《数学通讯》2018年第七期问题征解361题) 已知正实数x,y,z 满足x+y+z=1, 若不等式恒成立,求M 的最小值.

解构造函数:即为定义域上的凹函数,由琴生不等式:

所以M 的最小值为1.

例2(《数学通讯》2018年第七期问题征解364 题)已知正数ai(i=1,2,··· ,n,2n ∈N∗)满足a1a2···an=1,求证:

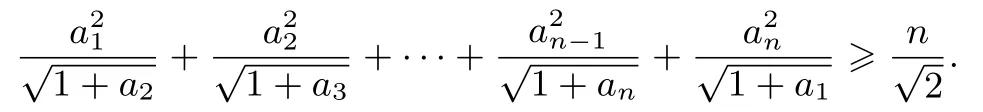
证明不妨设a1a2···an,则:由排序原理:

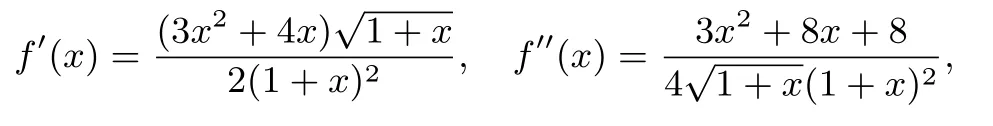
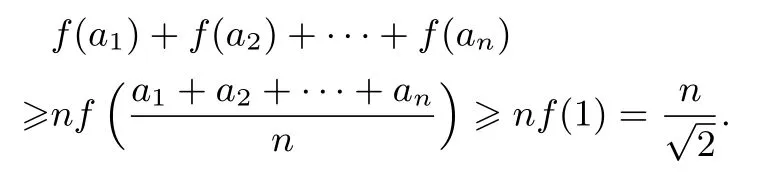
其中最后一步应用了均值不等式:

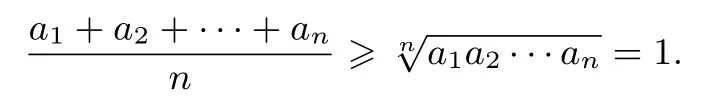
下面不等式的命制方法也是根据琴生不等式来命制的,读者不妨体会一下.

(1) (安振平新浪博客不等式问题4499 题) 设a,b,c ∈R+且a+b+c=1,求证:

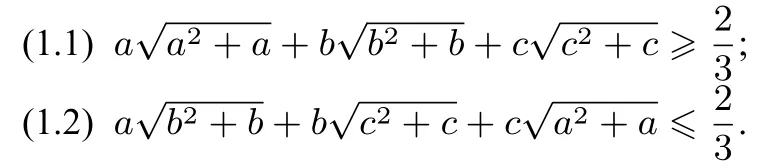
2.嵌入不等式

首先介绍一下嵌入不等式: 设A,B,C 为任意三角形的三个内角, x,y,z 为任意实数.则有: x2+y2+z22xy cos C+2yz cos A+2zx cos B.

简证x2+y2+z2−(2xy cos C+2yz cos A+2zx cos B)=(x−y cos C−z cos B)2+(y sin C−z sin B)20.

例3( 2018年全国高中数学联赛安徽省初赛第11题)(1) 求证: 对于任意实数x,y,z,都有: x2+2y2 +3z2

简析从试题的结构,我们一眼就能看出来,这道试题是利用嵌入不等式来命制的.解题时先从第二问入手,即解决问题的一般情形: 即是否存在实数使得对于任意实数x,y,z,x2+2y2+3z2k(xy+yz+zx)恒成立? 结合嵌入不等式:

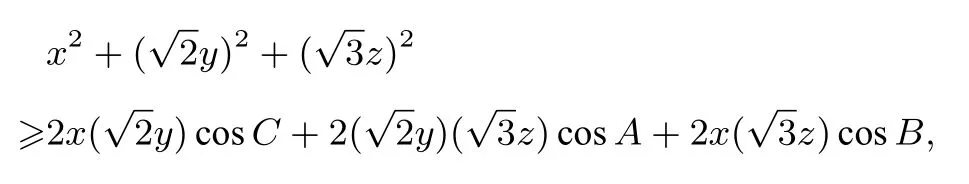
其中A,B,C 为任意三角形的三个内角.所以有:

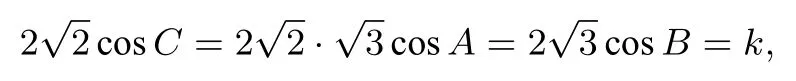
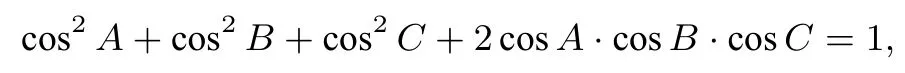
又由三角形恒等式:得: k3+6k2−24=0 且由得k2−8 < 0.构造存在实数使得k2−8<0,k3+6k2−24=0,从而结论成立.即存在实数使得对任意实数x,y,z,x2+2y2+3z2k(xy+yz+zx)恒成立.

例4(安振平不等式问题4528), 设正实数x,y,z 满足: xy+yz+zx+xyz=4, a,b,c 为任意实数, 求证:a2x+b2y+c2zabxy+bcyz+cazx.

证明由条件得:

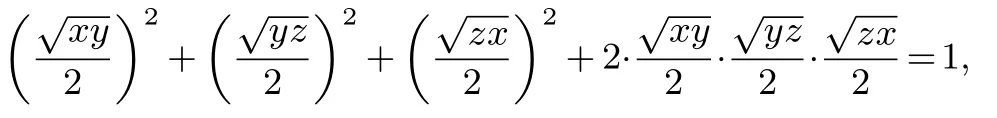
结合三角形恒等式:

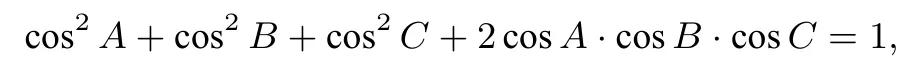
故可设:

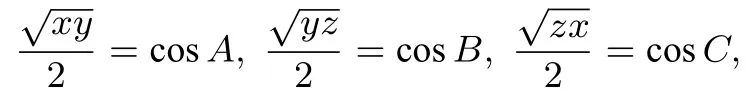
其中A,B,C 为锐角三角形的三个内角, 解得: x =

要证:

即证:

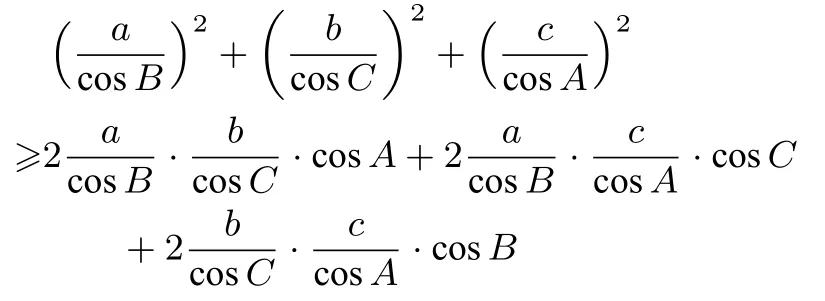
由嵌入不等式, 上式成立.所以: a2x+b2y+c2zabxy+bcyz+cazx.

下面不等式的命制方法也是根据嵌入不等式来命制的,读者不妨体会一下.

(2) (安振平不等式问题4529) 设正实数a,b,c 满足: a2+b2+c2+abc=4, x,y,z 为任意实数, 求证:ayz+bzx+cxyx2+y2+z2.

(3) (安振平不等式问题4527)设a,b,c > 0,x,y,z > 0,a2yz+b2zx+c2xy+abcxyz4,求证:

3.舒尔不等式

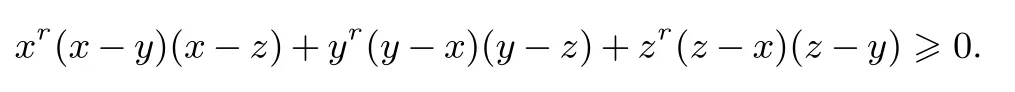
这就是著名的舒尔不等式, 我们经常所看到的是它的特殊形式, 即r=1 时的情形: x,y,z0, 则x(x−y)(x−z)+y(y−x)(y−z)+z(z−x)(z−y)0.

简证不妨设xyz.

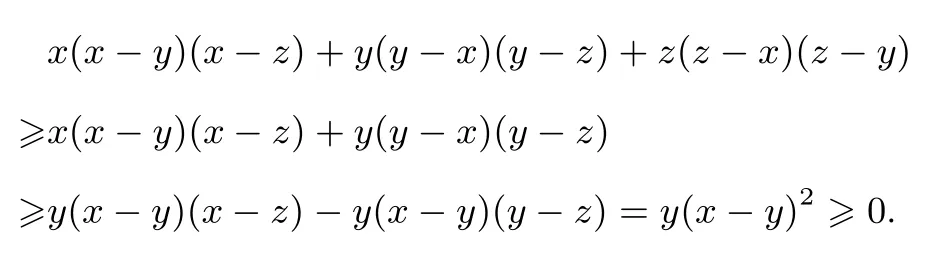
舒尔不等式还有几种常见的变式,证明的过程交给读者.

变式一x3+y3+z3+3xyzx2(y+z)+y2(x+z)+z2(x+y).

变式二xyz(x+y−z)(x+z−y)(z+y−x).

变式三(x+y+z)3+9xyz4(xy+yz+zx)(x+y+z).

变式四−(x2+y2+z2).

变式五

例5(《数学通讯》2013年第1-2 期问题征解124 题)设a,b,c > 0, abc=a+b+c+2, 求证: a+b+c

证明

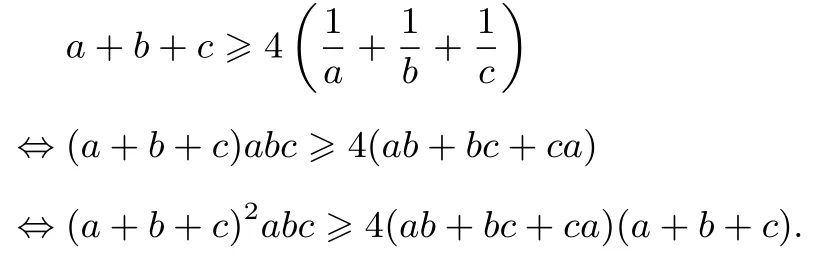
由舒尔不等式: (a+b+c)3+9abc4(ab+bc+ca)(a+b+c),只需证: (a+b+c)2abc(a+b+c)3+9abc, 由abc =a+b+c+2,所以原不等式等价于:

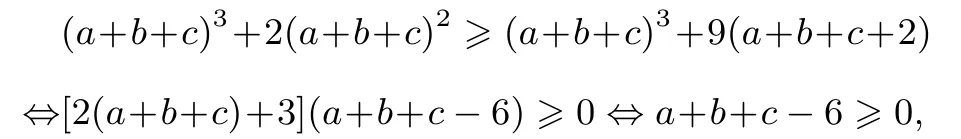
例6(《数学通讯》2018年第7 期问题征解354 题)已知a,b,c 为非负实数,且ab+bc+ca=a+b+c>0,求证:

证明⇔a+b+c+5abc由舒尔不等式:

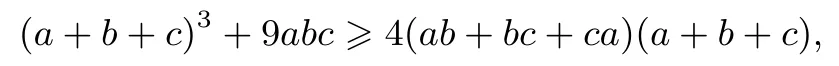
变形:

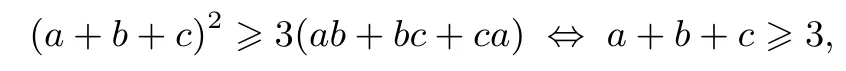
所以

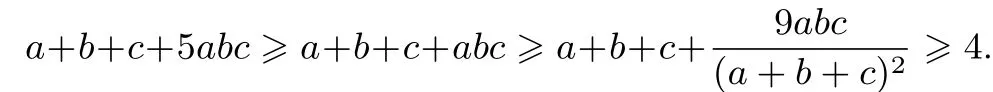
下面不等式的命制方法也是根据舒尔不等式来命制的,读者不妨体会一下.

(4) (安振平不等式问题4477)已知a,b,c>0,求证: