探索任意四边形的余弦定理
田传弟
(江苏省徐州市铜山区三堡中学 221112)
三角形的三边之间的关系可以用余弦定理表达出来,那么四边形的4条边和2条对角线之间是否存在类似的结论呢?
1 在一组对角互余的四边形中探求结论
在一组对角互余的四边形中有如下命题:

图1
如图1,在四边形ABCD中,∠BAD+∠BCD=90°,AC,BD为对角线,试证明
AC2·BD2=
AB2·CD2+AD2·BC2.
通过网络搜索发现,已有人证明过该命题,作者在证明时构造了辅助圆,构图复杂,证明过程也比较繁琐[1].下面给出简洁证明.
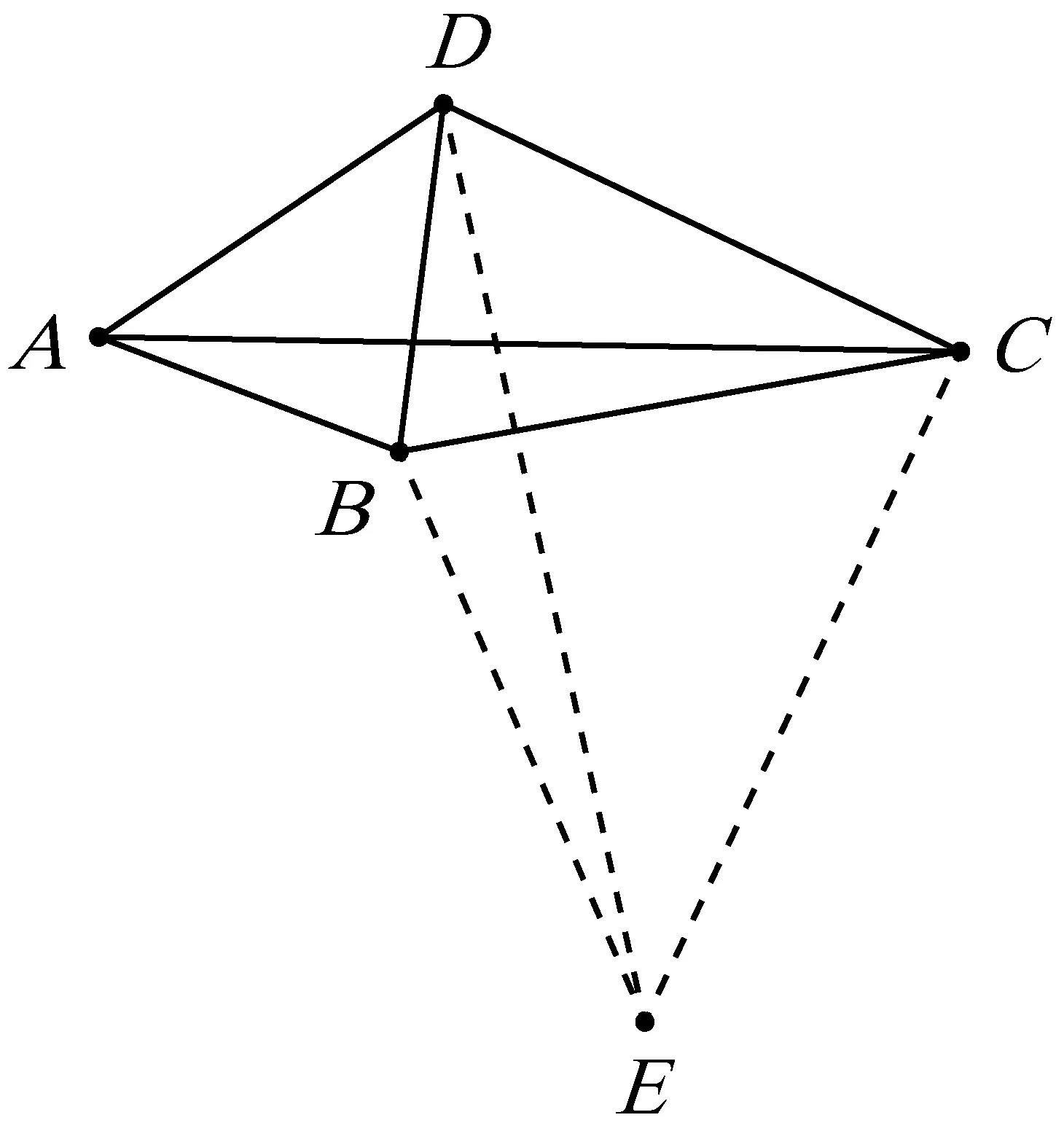
图2
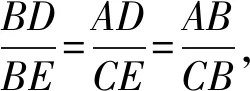
对角互余的的四边形的4条边和2条对角线之间的关系得以解决.
2 在一组对角之和为定值的四边形中探求结论
笔者进一步思考:若四边形的一组对角之和为定值,那么四边形的4条边和2条对角线之间的关系会有怎样的关系?经历一番探索之后,发现如下优美的结论:
如图3,若在四边形ABCD中,∠BAD+∠BCD=α,AC,BD为对角线,则
AC2·BD2=AB2·CD2+AD2·BC2-2AB·BC·CD·DAcosα.
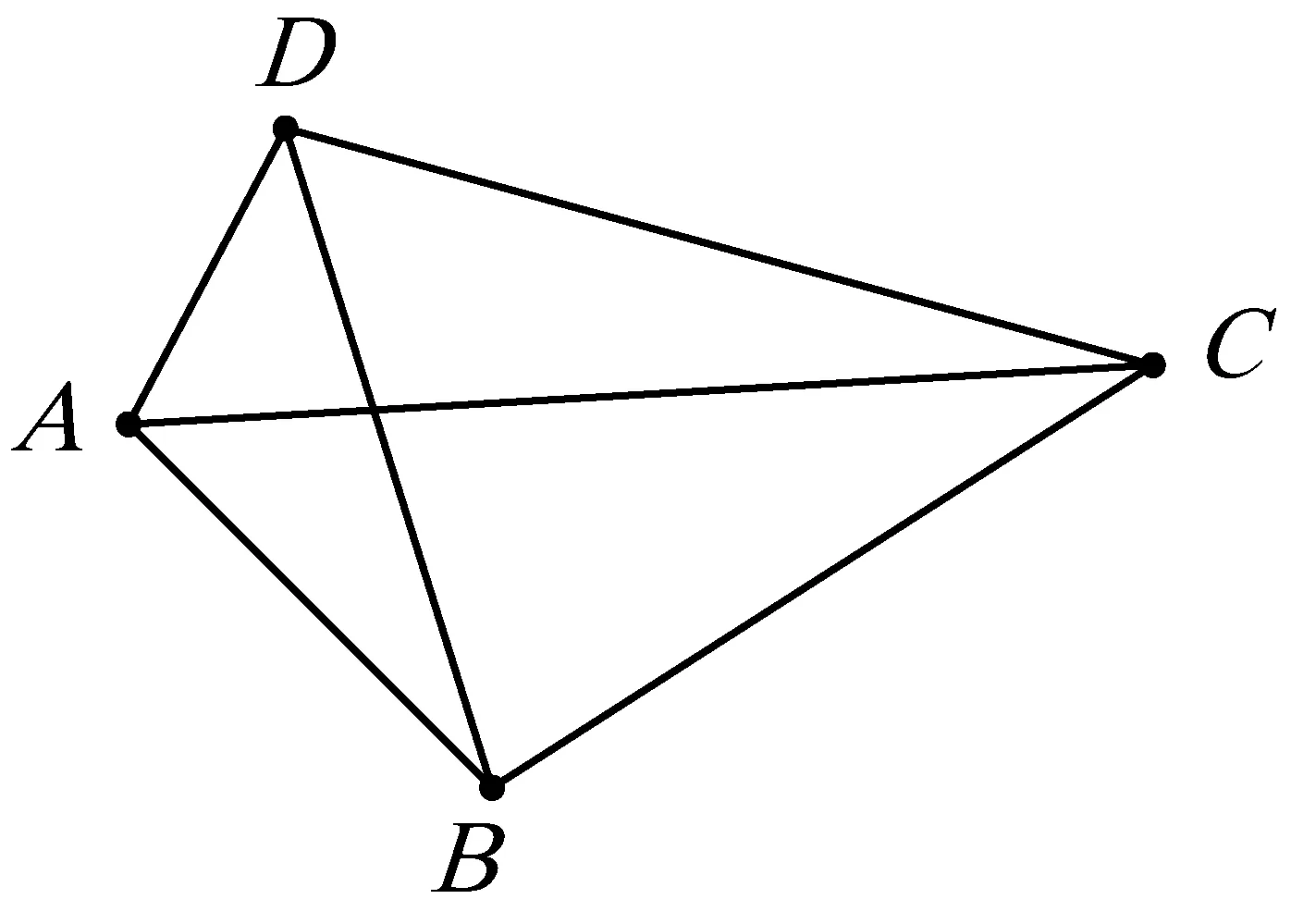
图3

图4
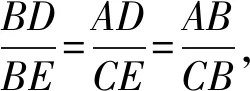
DE2=CD2+CE2-2CD·CEcosα,
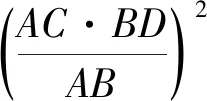
所以AC2·BD2=AB2·CD2+AD2·BC2-2AB·BC·CD·DAcosα.
看看特例:
当α=90°时,即是一组对角互余的特例,cos90°=0,因此结论是AC2·BD2=AB2·CD2+AD2·BC2;
当α=180°时,cos180°=-1,
所以AC2·BD2=AB2·CD2+AD2·BC2+2AB·BC·CD·DA,
所以(AC·BD)2=(AB·CD+AD·BC)2,即AC·BD=AB·CD+AD·BC,这个特例便是赫赫有名的托勒密定理.
上述结论是在凸四边形中研究和证明的,研究发现,它在凹四边形情形仍然成立.
如图5,在凹四边形ABCD中,∠BAD+优角∠BCD=α,AC,BD为对角线.试证明AC2·BD2=AB2·CD2+AD2·BC2-2AB·BC·CD·DAcosα.
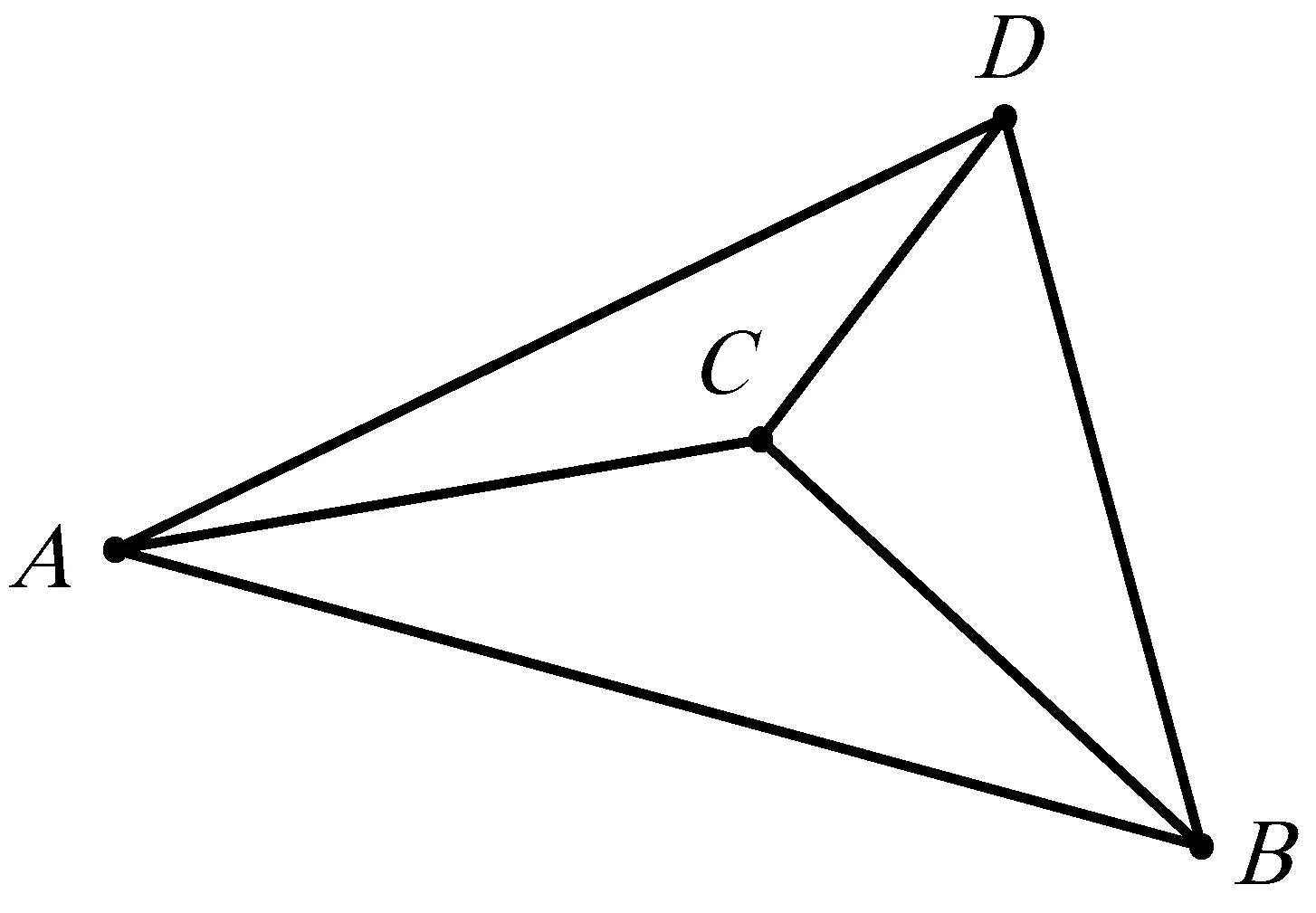
图5
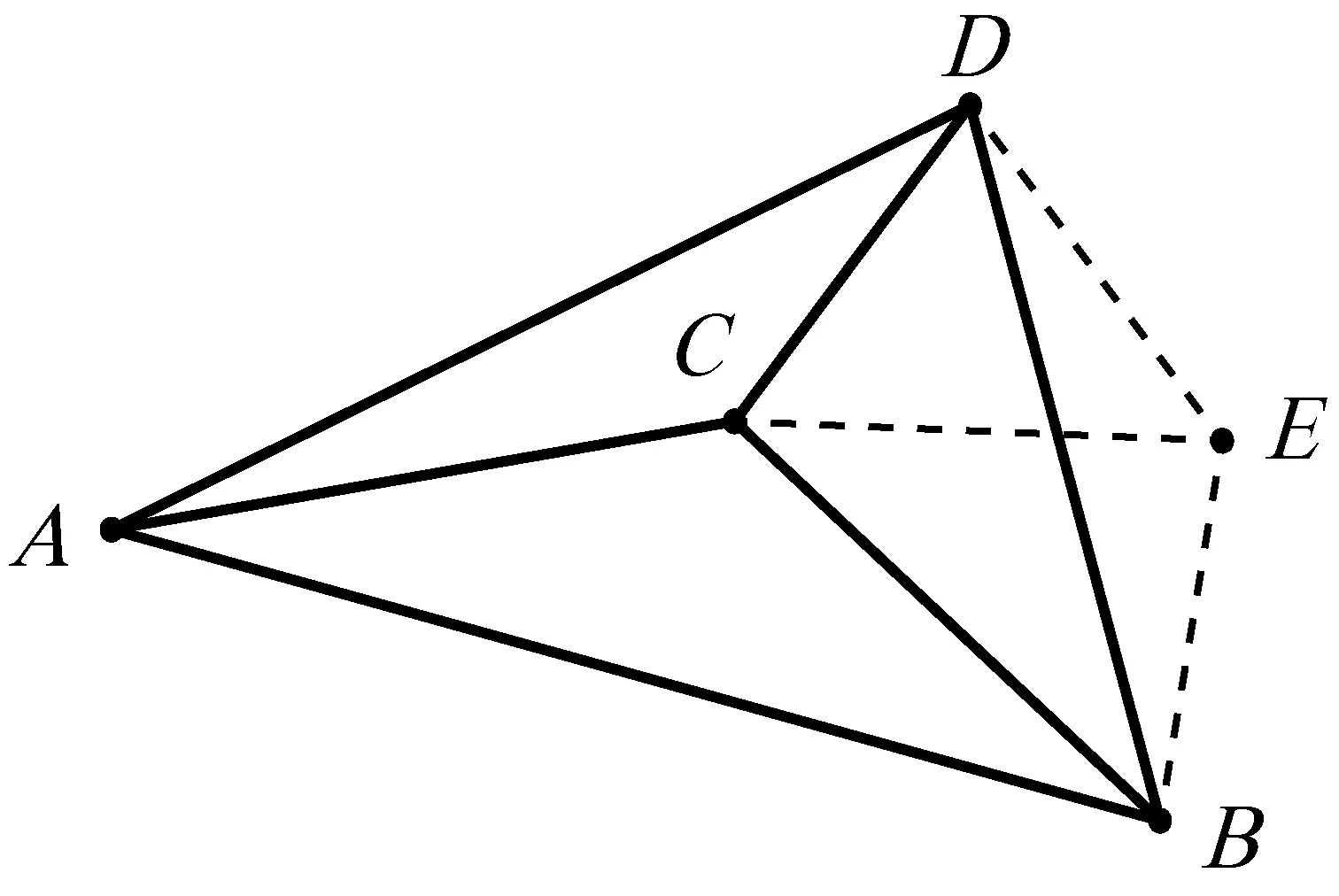
图6
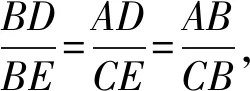

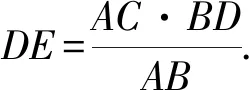
因为∠BAD+优角∠BCD=α,所以
∠DCE=360°-(优角∠BCD+∠BCE)
=360°-(优角∠BCD+∠BAD)
=360°-α,
在△DCE中,根据余弦定理,
DE2=CD2+CE2-2CD·CEcos∠DCE,

所以AC2·BD2=AB2·CD2+AD2·BC2-2AB·BC·CD·DAcosα.
综上所述,得到结论:
在任意四边形ABCD中,若一组对角之和为α,AC,BD为对角线,则
AC2·BD2=AB2·CD2+AD2·BC2-2AB·BC·CD·DAcosα.
一个如此优美的结论必须给它一个贴切的名字——四边形的余弦定理.

