任凭函数多变幻 求导原则不能撼
王芝平
(北京宏志中学 100013)
函数导数综合性问题一般都要回归函数单调性的判断,而判断一个复杂函数的单调性恰是函数导数的功能之一.
解决函数导数问题一般要经历“分析问题、构建函数、研究函数、解决问题”几个环节.
1.分析问题 首先要弄明白我们的目的是什么?即要解决的问题是什么?它能转化成什么等价问题(熟悉或易解决的)?
2.构建函数 为了解决上面问题,要构建恰当函数,使所构建的函数既能反映问题的本质,又更易于解决问题.
3.研究函数 一般要借助导数研究这个函数的单调性.函数导数在其零点左右两侧取值异号,那么该零点就是函数单调增、减区间的“分界点”,也必是函数极值点,进而有可能是函数的最值点.
4.解决问题 通过获得的函数性质解决问题.
例1(2010,全国Ⅰ,理20) 已知函数f(x)=(x+1)lnx-x+1.
(Ⅰ)略;
(Ⅱ)证明:(x-1)f(x)≥0.
谋定思路有方向
利用符号法则,将(x-1)f(x)拆分为两个函数x-1与f(x),分别研究它们的取值正负情况.这里我们返璞归真从最直接的方法入手:欲证F(x)=(x-1)f(x)≥0成立,只需证明函数F(x)的最小值非负即可,注意到F(1)=0,我们可以猜测F(x)的最小值为F(1),即F(x)在区间(0,1]上是减函数,而在区间[1,+∞)上是增函数,也就是F′(x)的值以1为“界”“先负后正”.这个想法可以反复使用,让我们试一试吧!
规范解答不失分
(Ⅱ)解 令F(x)= (x-1)f(x)(x>0),

因为F′(1)=0,所以F′(x)如果是增函数,那么我们的“小目标”就会得以实现.“函数单调不单调,导数正负破玄妙”,让我们看看函数F′(x)的导数的是正的还是负的吧!

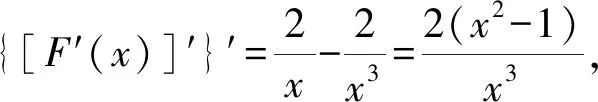
所以{[F′(x)]′}′>0⟺x>1,
{[F′(x)]′}′<0⟺0 所以[F′(x)]′在区间(0,1]上是减函数, 而在区间[1,+∞)上是增函数. 所以[F′(x)]′≥[F′(1)]′=2>0, 所以F′(x)是增函数. 因为F′(1)=0, 所以F′(x)>0⟺x>1,F′(x)<0⟺0 所以F(x)在区间(0,1]上是减函数, 而在区间[1,+∞)上是增函数. 所以F(x)≥F(1)=0, 即(x-1)f(x)≥0恒成立. 上述过程虽然艰难曲折,但是对导数的功能却有了更深层次的切身感悟,让我们充分体会到“任凭函数多变幻,求导原则不能撼——函数单调不单调,导数正负破玄妙”,简单地说,如果想知道一个函数的单调性,那么就看看其导数的正负吧! 可谓“不忘初心,方得始终”! 例2(2018,全国Ⅲ,理21) 已知函数f(x)=(2+x+ax2)ln(1+x)-2x. (Ⅰ)若a=0,证明:当-1 (Ⅱ)若x=0是f(x)的极大值点,求a. 解(网上流传的官方答案) 当-1 当x>0时,g′(x)>0. 故当x>-1时,g(x)≥g(0)=0, 且仅当x=0时,g(x)=0, 从而f′(x)≥0,且仅当x=0时, f′(x)=0.所以f(x)在(-1,+∞)单调递增. 又f(0)=0,故当-1 f(x)<0;当x>0时,f(x)>0. (2)(i)若a≥0,由(1)知,当x>0时,f(x)≥(2+x)ln(1+x)-2x>0=f(0),这与x=0是f(x)的极大值点矛盾. 故h(x)与f(x)符号相同. 又h(0)=f(0)=0, 故x=0是f(x)的极大值点当且仅当x=0是h(x)的极大值点. h′(x)>0,故x=0不是h(x)的极大值点. 所以x=0不是h(x)的极大值点. 如果6a+1=0, 则当x∈(-1,0)时,h′(x)>0; 当x∈(0,1)时,h′(x)<0. 所以x=0是h(x)的极大值点, 从而x=0是f(x)的极大值点. 下面给出我们的分析与解法. (Ⅰ)易知f(0)=0,由结论可知,只需证明a=0时f(x)是增函数即可,进而考察f′(x)是否恒不小于0.如果不易发现f′(x)的正负,可继续讨论函数f′(x)的导函数取值情况,这个过程可反复进行. (Ⅱ) 因为x=0是f(x)的极大值点,又f(x)是可导函数,由极值点的定义及极值点与函数导数的关系可知,f′(0)=0且f′(x)在x=0的左右两侧的取值符号应该是“左正、右负”,所以f′(x)在以0为中心的一个区间(如(-b,b))上是减函数.这就要继续研究f′(x)的导函数[f′(x)]′是否小于0,如果不达目的,可如法炮制继续研究[f′(x)]′的导函数. 也可以综合利用“复杂函数大于零,符号法则立奇功”与“不等结构任纷杂,适当分离变通达”等策略,将函数f(x)转化为较为简单的函数予以研究. 规范解答不失分 解(Ⅰ)函数f(x)的定义域为 (-1,+∞) . 当a=0时,f(x)=(2+x)ln(1+x)-2x, 当-1 当x>0时,g′(x)>0. 故当x>-1时,g(x) ≥g(0) =0, 且仅当x=0时,g(x)=0, 所以g(x)=f′(x)在区间(-1,0)上是减函数, 在区间(0,+∞) 上是增函数, 从而f′(x)≥f′(0)=0, 且仅当x=0时,f′(x)=0. 所以f(x)在(-1,+∞)单调递增. 又f(0)=0,故当-1 f(x)<0;当x>0时,f(x)>0 (Ⅱ)方法1 (i)若a≥0,由(1)知,当x>0时,f(x)≥(2+x)ln(1+x)-2x>0,这与x=0是f(x)的极大值点矛盾. 因为若x=0是f(x)的极大值点, 所以f′(x)在x=0的左右两侧的取值符号应该是“左正、右负”, 所以f′(x)在以0为中心的一个区间上是减函数. 这就要再研究f′(x)的导数, 我们希望[f′(x)]′<0, 那么x=0是[f′(x)]′的极大值点. 同理{[f′(x)]′}′在x=0处的导数等于0,且在x=0左右两侧的取值符号应该是“左正、右负”, 所以,当-1 当0 即当-1 当且仅当x=0时,[f′(x)]′=0. 所以f′(x)在区间(-1,1)上是减函数. 又因为f′(0)=0, 所以当-1 当0 所以f(x)在区间(-1,0)上是增函数,在区间(0,1)上是减函数, 所以x=0是f(x)的极大值点,该极大值为f(0)=0. (Ⅱ)方法2 (i)若a≥0,由(1)知,当x>0时,f(x)≥(2+x)ln(1+x)-2x>0,这与x=0是f(x)的极大值点矛盾. (ii)若a<0,注意到函数f(x)的复杂性,可将2+x+ax2与ln(1+x)进行“分离”. 先研究函数r(x)=2+x+ax2的一些基本特征: 因为a<0,所以二次函数r(x)的图像开口向下, 又Δ=4-8a>0,r(0)=2>0, 所以存在一个区间(-b,b)(0 在这个区间上r(x)>0, 因为f(x) =(2+x+ax2)ln(1+x)-2x 因为x=0是f(x)的极大值点, 即f(x)≤f(0)=0, 又h(0)=0, 所以“x=0是f(x)的极大值点”等价于“x=0是h(x)的极大值点”. 这等价于h(x)在(-b,0)上是增函数, 在(0,b)上是减函数, 即在(-b,0)上,h′(x)>0, 在(0,b)上h′(x)<0,且h′(0)=0. 令p(x)=a2x2+4ax+6a+1 (-b 则x=0不是h(x)的极大值点. 即若x=0是h(x)的极大值点, (必要条件) 所以h′(x)>0⟺p(x)>0⟺-b 所以h(x)在区间(-b,0)上是增函数,在区间(0,b)上是减函数, 所以x=0是h(x)的极大值点, 即x=0是f(x)的极大值点. (充分条件) 利用导数研究函数性质时,要明白求导的目的与意义是什么?不能让求导成为一种僵化的解题模式,求导之后就不知道干什么了,这归根结底还是没有从本质上理解导数工具能为我们分析函数带来什么.上面的解法不同于标准答案,其特点是不断分析新的目标函数应该正负如何,单调性如何,指引的非常清晰,解题很有目标感.这就是所谓的“发现问题、提出问题、分析问题、解决问题”的能力吧. 在上述解法中,虽然多次构造新的函数、多次求导,但是它们都不是解决问题的本质核心,核心是我们想研究函数的什么,我们用什么工具手段来研究,从这点来说,三次求导虽然罕见,但是并不是新鲜的题型,而是对于“原则”的合理运用,“任凭函数多变幻,导数原则不能撼”正是一针见血的点明了这一点. 再次表明我们的态度:“任凭函数多变幻,求导原则不能撼——函数单调不单调,导数正负破玄妙”.解后反思要升华




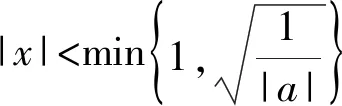
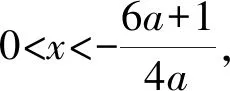
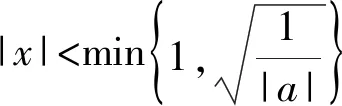
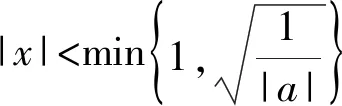
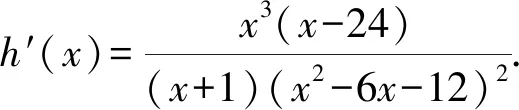

谋定思路有方向
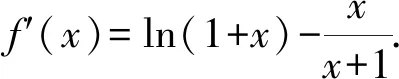

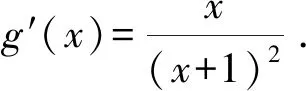
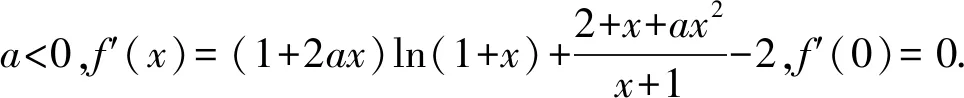

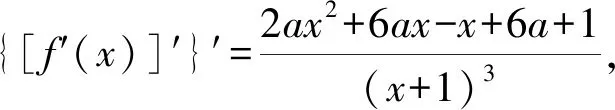





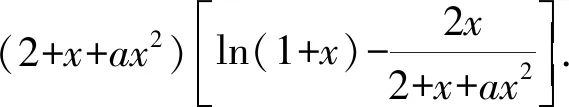
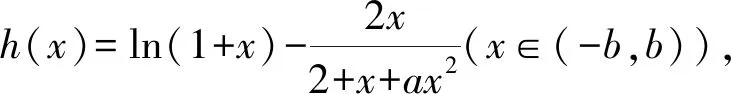






解后反思要升华

