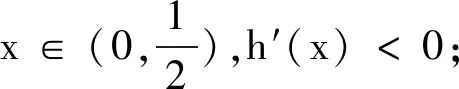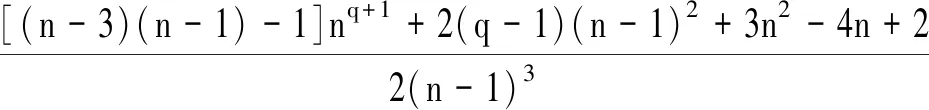一类条件代数不等式统一推广的拾遗
李汝雁 郭要红 孟庆利
(安徽师范大学数学计算机科学学院 241000)
文[1]从项数与指数出发,对本刊2009年第8期数学问题1808[2]与2010年第1期数学问题1833[3]进行了如下推广:

(1)
文[4]从指数出发,对上述问题1808、问题1833与本刊2015年第4期数学问题2238[5]给出了如下推广:
定理2设a,b>0,且a+b=1,对任意的正整数m,n(m≥2),则有
(2)
文[6]从指数与项数入手,给出不等式(1)、(2)的一个统一推广如下:.

(3)
在文[6]的上述定理3的证明中,条件p≥2是必要的,考虑p=1时,(3)式是否成立?我们得到定理3的如下拾遗:

(4)
证明分n=2,q≥3;n=3;n≥4三种情形证明.
(Ⅰ) 当n=2,q≥3时,

其中b0=2q+1-1-(q+1).

当q≥3时,b0>0,
b0+b1=2(2q+1-1)-(q+1)(1+2q)
≤2(2q+1-1)-4(1+2q)
=-6<0,
b0+b1+b2
=3(2q+1-1)-(q+1)(1+2q+2q-1)
≤3(2q+1-1)-4(1+3·2q-1)
=-7<0,…,
b0+b1+b2+…+bq-1
=q(2q+1-1)-(q+1)(1+2q+2q-1+…+22)
=q(2q+1-1)-(q+1)(2q+1-22+1)
=-[2q-1-(q+1)]·22-q-(q+1)<0,
b0+b1+b2+…+bq-1+bq
=(q+1)(2q+1-1)-(q+1)(1+2q+2q-1+…+22+2)
=0.
由b0+b1+b2+…+bq-1+bq=0,得
b0xq+b1xq-1+b2xq-2+…+bq-1x+bq
=(x-1)[b0xq-1+(b0+b1)xq-2+(b0+b1+b2)xq-3+…+(b0+b1+b2+…+bq-1)]
当q=3,因为x∈(0,1),
b0xq-1+(b0+b1)xq-2+(b0+b1+b2)xq-3+…
+(b0+b1+b2+…+bq-1)
=b0x2+(b0+b1)x+(b0+b1+b2)
=11x2-6x-7
<11x-6x-7
=5x-7<0.
当q>3,因为x∈(0,1),b0+b1+b2<0,…,b0+b1+b2+…+bq-1<0,
b0xq-1+(b0+b1)xq-2+(b0+b1+b2)xq-3+…
+(b0+b1+b2+…+bq-1)
=[b0x+(b0+b1)]xq-2 <(2b0+b1)xq-2 =[2q+2-2-2(q+1)+2q+1-1-(q+1)2q]xq-2 =[(4-q)-(5+2q)]xq-2<0. (5) 由(5)式,有 (6) (7) 将(6)、(7)两式相加,并注意到a1+a2=1,得 (Ⅲ) 当n≥4,因为 而 (8) (9) u=n+2n2+…+(q-1)nq-1+qnq, nu=n2+…+(q-1)nq+qnq+1, (1-n)u=n+n2+…+nq-qnq+1 v=q-1+(q-2)n+…+nq-2, nv=(q-1)n+(q-2)n2+…+nq-1, (n-1)v=n+n2+…+nq-1-(q-1) w=nq, w-v u+v-w =(q-1)s≥0, >0. 所以 (由(8)式) 综合(Ⅰ)、(Ⅱ)、(Ⅲ)知,定理4成立.证毕.