一类具有双时滞四维捕食模型的定性分析

武利青， 王晓云

(太原理工大学 数学学院， 山西 太原 030024)

0 引 言

捕食模型主要研究种群之间, 种群和环境之间的相互关系, 这对生态系统的发展与保护具有非常重要的意义. 在捕食系统中最经典的是洛特卡和沃尔泰提出的 Lotka-Volterra 模型, 简称 L-V 模型. 近年来, 由于 L-V 模型在种群动力学的研究中发挥了举足轻重的作用, 因此许多学者在此模型的基础上进行了改进和延伸, 并取得了很好的成果. 文献[1-3] 对具有单时滞的二维捕食模型的稳定性和 Hopf 分支的存在性等问题做了分析, 文献[4] 研究了双时滞二维捕食模型的稳定性, 周期解的存在性和分支方向问题. 文献[5-7] 对具有阶段结构的单时滞的三维捕食模型的稳定性和分支的存在条件做了深度研究, 文献[8] 对具有时滞和基于比率的三种群捕食模型的全局渐近稳定性进行了分析. 在文献[9] 中, 讨论了一类具有单时滞的四维捕食模型的稳定性与分支的存在性. 然而, 双时滞的四维捕食模型的探究非常罕见, 如果能考虑双时滞高维的食物链系统, 则系统的动力学性质将变得更加丰富.

典型的 Lotka-Volterra 模型

(1)

式中：x1(t),x2(t)分别表示在t时刻食饵和捕食者的种群密度; 参数a10,a12,a20,a21均为正常数. 由于捕食时间、成熟期和怀孕期等时滞因素对捕食-食饵模型中种群的稳定性有非常重要的作用, 同时通过调节时滞可使捕食者和食饵达到永久续存的状态, 因此我们将时滞引入捕食模型进行研究. 考虑三个因素: ① 种群密度越高, 捕食率随食饵密度的增加而增加; ② 捕食者追捕时间直接影响食饵的数量; ③ 成熟期即捕食者只有到成年才具有捕食能力. 基于以上考虑, 本文研究食饵均有密度制约项的四维捕食模型, 而且将种群间的追捕时间和成熟期列为时滞因素加入模型. 其改进的模型为

(2)

式中：x1(t),x2(t),x3(t),x4(t) 分别表示在t时刻一级食饵, 二级食饵, 三级食饵及捕食者四个种群的种群密度; 参数a10是一级食饵的内禀增长率,a20,a30是二级、三级食饵的死亡率,a40是捕食者的自然死亡率,a11,a22和a33是密度制约系数,a12,a23和a34是捕食系数,a21,a32和a43是消化率. 捕食者的变化情况取决于在之前一段时间内食饵和捕食者的数量， 假设x2,x3和x4这三个种群均有相同的追捕时间τ1和相同的成熟期τ2, 并且满足τ1+τ2=τ.

初值满足条件

1 正平衡点的局部稳定性

考虑到系统 (2) 中各种群的生态学意义, 本节研究它的正平衡点.

(3)

其中

证明若系统 (2) 存在平衡点, 则应满足方程组

(4)

(5)

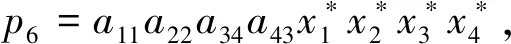
(6)

通过计算可得系统(2)在正平衡点E*处的线性近似系统的特征方程

λ4+p1λ3+p2λ2+p3λ+p4e-λτλ2+p5e-λτλ+

p6e-λτ+p7e-2λτ=0.

(7)

当τ=τ1=τ2=0时, 系统(2)相应的特征方程式(7)为

λ4+p1λ3+(p2+p4)λ2+(p3+p5)λ+

(p6+p7)=0.

(8)

由Routh-Hurwitz准则[10]可知, 当满足H1,H2,H3,H4均大于0时, 特征方程(8)的所有根均有负实部.

H1∶p1>0,

显然H1,H2恒大于 0.

由定理条件知H3>0.

(p6+p7)H3.

因为H3>0, 则H4>0. 因此, 由Routh-Hurwitz准则可得E*是局部渐近稳定的. 证毕.

定理3 若存在临界滞量τ0, 使当τ在τ0附近取值且τ<τ0时, 系统(2)(此时τ2=τ0-τ1, 系统 (2) 实质上是单时滯的) 在正平衡点E*处仍然保持稳定.

证明当τ>0时, 设λ=iw(w>0)是特征方程(7)的一个纯虚根, 代入式(7)可得

(w4-p2w2+p7)coswτ+(p1w3-p3w)sinwτ-p4w2+p6+

[(p3w-p1w3)coswτ+(w4-p2w2-p7)sinwτ+p5w]i=0.

(9)

分离式(9)的实部和虚部， 得

(10)

计算可得

(11)

其中

d5=-p5+p1p4,d6=p2p5-p3p4-p1p6,

d7=p3p6-p5p7,d8=p4,

d9=-p2p4-p6+p1p5,

d10=-p4p7+p2p6-p3p5,d11=p6p7.

由sinwτ2+coswτ2=1, 可知

w16+f1w14+f2w12+f3w10+f4w8+

f5w6+f6w4+f7w2+f8=0,

(12)

其中

f5=2d1d4+2d2d3-2d8d11-2d9d10-

令z=w2, 则式(12)变为

z8+f1z7+f2z6+f3z5+f4z4+f5z3+

f6z2+f7z+f8=0.

(13)

根据Bulter[11]引理, 定理得证.

2 正平衡点的Hopf分支

系统(2)是具有双时滞的四维捕食模型, 下面讨论正平衡点E*在τ处的 Hopf 分支.

A=2p7wsinwτ-w2p5,

B=-p4w3+p6w+2p7wcoswτ,

C=-3p1w2coswτ+p3coswτ+4w2sinwτ-

2p2wsinwτ+p5,

D=-4w2coswτ+2p2wcoswτ-3p1w2sinwτ+

p3sinwτ+2wp4.

证明将λ=λ(τ)代入方程(7), 有

⟹

由于

3 数值模拟

将系统(2)中的参数取值a10=1.4,a20=a30=a40=0.2,a11=a22=a33=0.2,a12=a23=a34=

0.4,a21=a32=a43=0.3, 且满足H3>0时, 考虑以下系统

(14)

通过计算得正平衡点为E*(2.92,2.04,0.67,0.70),τ0=1.63. 取τ=0.88<τ0,τ1=0.53,τ2=0.35 时, 正平衡点E*是稳定的(见图 1);τ=τ0,τ1=0.93,τ2=0.70时, 正平衡点E*的稳定性受到破坏(见图 2);τ=1.68>τ0,τ1=1.53,τ2=0.15, 正平衡点E*是不稳定的(见图 3).

图 1 当τ=0.88<τ0, τ1=0.53, τ2=0.35时, 正平衡点E*稳定的分量图Fig.1 Component figure with τ=0.88<τ0, τ1=0.53, τ2=0.35 when the equilibrium is stable

图 2 当τ=τ0=1.63, τ1=0.93, τ2=0.7 时, 正平衡点E*附近产生分支的分量图Fig.2 Component figure with τ=1.63=τ0, τ1=0.93, τ2=0.7 when the equilibrium has bifurcation

图 3 当 τ=1.68>τ0, τ1=1.53, τ2=0.15 时, 正平衡点E*不稳定的分量图Fig.3 Component figure with τ=1.68=τ0, τ1=1.53, τ2=0.15 when the equilibrium loses its stability