基于TV范数的压缩感知光偏折层析重建
李化欣
(中北大学 信息与通信工程学院, 山西 太原 030051)
0 引 言
光学CT (光干涉CT、 光偏折CT等)是从多个方向上的投影数据进行二维或三维被测场分布的反演. 与干涉CT相比, 光偏折 CT具有宽动态测试范围, 适用于恶劣环境, 因此被广泛用于测量复杂流场[1-2]. 莫尔偏折层析技术测试动态范围大, 设备简单、 对机械稳定性要求低, 该技术适用于高温高速流场的测量[3-5]. 然而, 偏转层析成像的数学方面是复杂的, 正是这种复杂性阻碍了实际重建算法的发展. 计算偏折层析成像技术可分为变换方法和级数展开法. 当重建使用全场视角范围的大量等间隔投影数据时, 诸如滤波反投影方法的变换类算法可以获得更好的结果, 但这种方法难以处理不完全数据. 相比之下, 级数展开法[6], 尤其是代数重建技术[7](ART)更加实用, 因为它可以灵活地处理不完全的数据. 通过积分变换转换投影数据后, 以ART算法为代表的迭代算法, 对于不完全投影数据, 极少投影数据, 抑制噪声等方面比系列展开法更适合解决实际问题的重建. 近些年来出现的子集迭代重建算法[8], 定向代数重建技术[9]、 自适应联合代数重建技术[10]等算法不断改进着重建算法的性能. 但是这些都是CT的一般重建算法, 不能反映光偏折CT的基本特征. 将光偏折投影数据沿垂直于投影方向的积分可以获到光程差投影, 然后通过使用重建算法重建被测场. 但是, 在极少采样数据的情况下, 这类重建算法也不能重建出满足高精度指标的温度场. 在极少采样情况下研究CT重建过程时, 压缩感知(CS)对于信号处理是一种颠覆性的信息处理理论, 它开阔了研究人员的研究思路. 从Donoho和Candes提出的CS理论可以看出: 若信号或者图像在某一特定的变换域存在稀疏表示, 那么可以适当地优化从极少的投影数据重建出原来的信号或者图像[11]. 通过原始信号或者图像的随机投影而获得投影数据, 该投影数据远小于奈奎斯特采样定理所需的投影数据. 这样可以有效降低采样系统的复杂性, 节约系统成本, 加快信号或者图像的重建速度. 压缩感知的理论已经在数字图像重建[12-13]、 图像去除噪声等领域得到了应用, 而且该特性非常适合用于测量不稳定[14]、 复杂流场的极度欠采样重建.
本文针对偏折层析成像中极度欠采样条件下重建精度较低的问题, 结合 CS理论, 将被测场的全变分作为稀疏性先验模型, 利用最速下降法来调整全变分, 使得温度场的全变分最小化. Sidky[15]等人提出的自适应梯度下降法, 设置了很多参数来确定步长. 而本文在研究传统ART-TV算法的基础上, 稍微改进了算法的步长, 并采用一致性约束步长作为梯度下降法的步长, 使梯度自适应下降. 并把该方法用于重建模拟温度场并分析重建误差, 验证算法的有效性. 对于稀疏投影数据的被测场重建, 本文改进的算法重建质量和抗噪声能力比ART-TV算法更好.
1 原 理
1.1 偏折信息的转化
如图 1 所示, 设被测场某截面的折射率分布为
(1)
式中:n0为环境折射率,f(x,y)为相对折射率分布. 如图 1 所示将坐标系x-y逆时针旋转θ角后得到坐标系x′-y′. 当平行于x′轴的入射光线经过被测场时, 光沿着y′方向的偏折角为
(2)
该光线通过被测场的光程差为
(3)
式中:l是光线经过被测场的光程. 当光以小角度偏转时, 光可以近似为被测场区域中的直线.

(4)
因此, 积分运算可以将偏折投影数据转化为光程差投影数据,即

(5)

图 1 光线偏折原理与坐标系示意图Fig.1 Schematic diagram of the beam deflection and coordinate system
将重建区域划分为k=N×N个网格, 将每个网格中的折射率变化设置为常数, 并设置总投影方向为q, 每一个方向的采样数为r, 这样总采样数为m=q×r. 通过(5)可以将偏折投影方程转换为光程差投影方程.
(6)
式中:Aij是第i条光线通过第j个网格的长度;pi是通过偏折角转化得到的第i条光线的投影数据.
1.2 ART-TV算法
压缩感知从通过随机投影获得的少量投影数据中重建信号. 重建是在满足观测值的条件下找到最稀疏解的过程, 图像或分布矩阵用f表示, 那么投影观测值表示为P=Af,Ψ代表某一稀疏变换, 投影矩阵用A表示, 此处的Ψ和A是不相干的. 则通过求解式(7)就可重建原始分布.
(7)
式中零范数‖·‖0表示非零元素的数量. 式(7)是典型的非凸优化问题, 因为此问题的求解过程相当困难, 所以Candés和Donoho 提出了采用范数l1代替l0范数[16-17], 式(7)变为
(8)

根据压缩感知的原理以及偏折角的变换, 用有限差分作为稀疏变换, 结合物理量(温度、 密度)分布总变差的稀疏性, 通常通过总变差TV(Total Variation)来衡量, 并且式(8)中的‖Ψf‖1就成为‖f‖TV, 如式(9)所示
(9)
其中
式中:f表示折射率的分布矩阵;s,t是矩阵f的坐标序号; 矩阵A是光线通过网格的长度. ART-TV算法的流程如下:
1) 取初始值f(0)=0, 从已知角度投影数据进行ART迭代, 得到初始被测场的分布
j=1,2,…,k.
(10)

(11)
3) TV梯度下降
初始化TV梯度下降法
f(TV-GRAD)=f(ART-POS),
(12)
d=‖f(0)-f(ART-POS‖.
(13)
TV求导
(14)

(15)
式中:α为梯度下降法的松弛因子;d表示在正约束之后得到的折射率与不受约束的折射率的差值.
4) 将TV下降处理后的值赋值给ART作为迭代的初值, 进行下一次迭代
f(0)=f(TV-GRAD).
当d的差异足够小或一定次数的迭代时, 迭代结束.
1.3 一致性控制步长算法
本文的算法是对TV最小化过程中梯度下降法中的步长进行一致性控制, 可以根据被测场的重建质量自动更新迭代步长, 并且可以确保梯度下降方向为被测场收敛的方向. 在初始迭代时, 投影数据存在很大的不一致性, 并且‖Af-P‖的值比较大, 所以可以增大迭代步长来使得f在可行域中; 当‖Af-P‖的值比较小时, 保证在约束的可行域中找到最优解. 所以我们希望通过数据的不一致性来确定梯度下降法中的步长. 一致性控制步长是基于被测场的原始投影数据与重建的投影数据之间的差, 以给出新的控制迭代步长.
在本方法中, 式(15)中的常数α可以由一致性控制步长函数η(n)来代替. 在本方法中, 修改后的梯度下降法为
(16)
其中
(17)
一致性控制步长函数η(n)在梯度下降的过程中不变, 只在ART开始迭代更新时修改. 式中f(0)是初始值, 在ART-TV开始迭代时n=1, 分子和分母的值一样,η(n)=1, 随着迭代次数的增多Af和P值逐渐接近, 因此, 步长从1开始, 并随着迭代次数的增加而逐渐减小.
2 实验与结果分析
2.1 温度场的评价标准
温度场重建的质量好坏可以通过均方根误差(Root Mean Square Error, RMSE)来衡量, RMSE越小说明重建效果越好. 用峰值误差(Peak Value Error, PVE)来评价温度场重建峰值的误差, PVE越小说明重建的峰值越好.
(18)

(19)

2.2 仿真实验
在本文的模拟仿真实验中, 采用满足高斯分布的三峰温度场函数
0 (20a) t(x,y)=0 其他. (20b) 如图 2 所示, 设网格数为30×30, 重建被测场区域的实际长度为30 cm×30 cm. 模拟环境温度为0 ℃, 实际上三个峰值的温度值分别为150, 200和250 ℃. 图 2 三峰高斯模拟温度场Fig.2 Three peak Gauss simulation of temperature field 在本文中, 采样以0°~180°的范围内的22.5°的间隔进行, 并且获得8个方向上的投影数据, 并且每个方向上的样本数量为40. 初始值为0, ART迭代算法中松弛因子λ=0.25, 并且在20次迭代后得到折射率的分布. 温度t和折射率n之间的关系可以通过G-D(Gladston-Dale)公式来确定. (21) 为了研究有噪声条件下本文算法的重建质量, 对带有白噪声的偏折角投影数据进行了仿真. 图 3 为两种算法的重建结果, 图 4 为两种算法在投影数据叠加了白噪声后的重建结果. 表 1 为两种算法重建后的误差. 图 3 无噪声的三峰温度场重建结果Fig.3 Three peak temperature field reconstructed without noise 图 4 有噪声的三峰温度场重建结果Fig.4 Three peak temperature field reconstructed with noise 表 1 两种算法的重建误差 从图 2 和图 3 的重建结果可以看出, 在8个投影方向的极度不完全数据的条件下, 不论在有噪声的情况下还是在没有噪声的情况下, 都可以看出本文算法重建出的表面质量明显都优于ART-TV算法. 而且本文算法可以更有效地重构峰值. 从表1的重建误差中可以看出, 迭代相同的次数, 不论是否存在噪声, 本文算法的RMSE更小, 说明本算法的收敛速度更快, 误差更小. 本文算法的误差PVE比ART-TV算法要小, 说明本文的算法可以更好、 更有效地重构出温度场的峰值. 从有噪声的误差中可以看出本文算法的误差RMSE和PVE都比ART-TV算法要小, 说明本文算法的抗噪声性能更好一些. 为了验证本算法的有效性, 将该算法用于液化石油气火焰温度场的重建. 实验数据由青岛科技大学流场光测实验室提供, 用莫尔偏折仪来获取多方向的莫尔条纹图, 实验装置见文献[4]. 图 5 6个不同方向的莫尔条纹图Fig.5 Morie deflectograms at six view angles 其中激光波长632.8 nm, 使用两个完全相同的Ronchi光栅, 莫尔条纹图成像在屏上, 然后再用CCD采集读入计算机. 在重建过程中将重建区域划分成30×30的网格, 使用本文提出的算法, 参数松弛因子取值为λ=0.55, 环境温度为20°, 使用从到等间隔的6个投影方向的投影数据重建, 每个投影方向下的采样数为150, 用本文改进的算法迭代20次后, 得到温度场的分布图, 如图 6 所示. 图 6 重建温度场Fig.6 Reconstructed temperature field 本文将偏折角转化的迭代算法与TV范数相结合, 在传统ART-TV算法的基础上, 对梯度下降法的步长稍作调整, 采用一致性控制步长, 使梯度下降. 通过对三峰温度场的仿真实验, 通过重建结果可以看出, 本文的算法重建的温度场平滑度优于ART-TV算法, 在峰值的构建方面表现出优越性, 并且可以更好地抑制噪声. 实验结果表明, 本文的算法对于极少投影方向的温度场的重建是有效的.

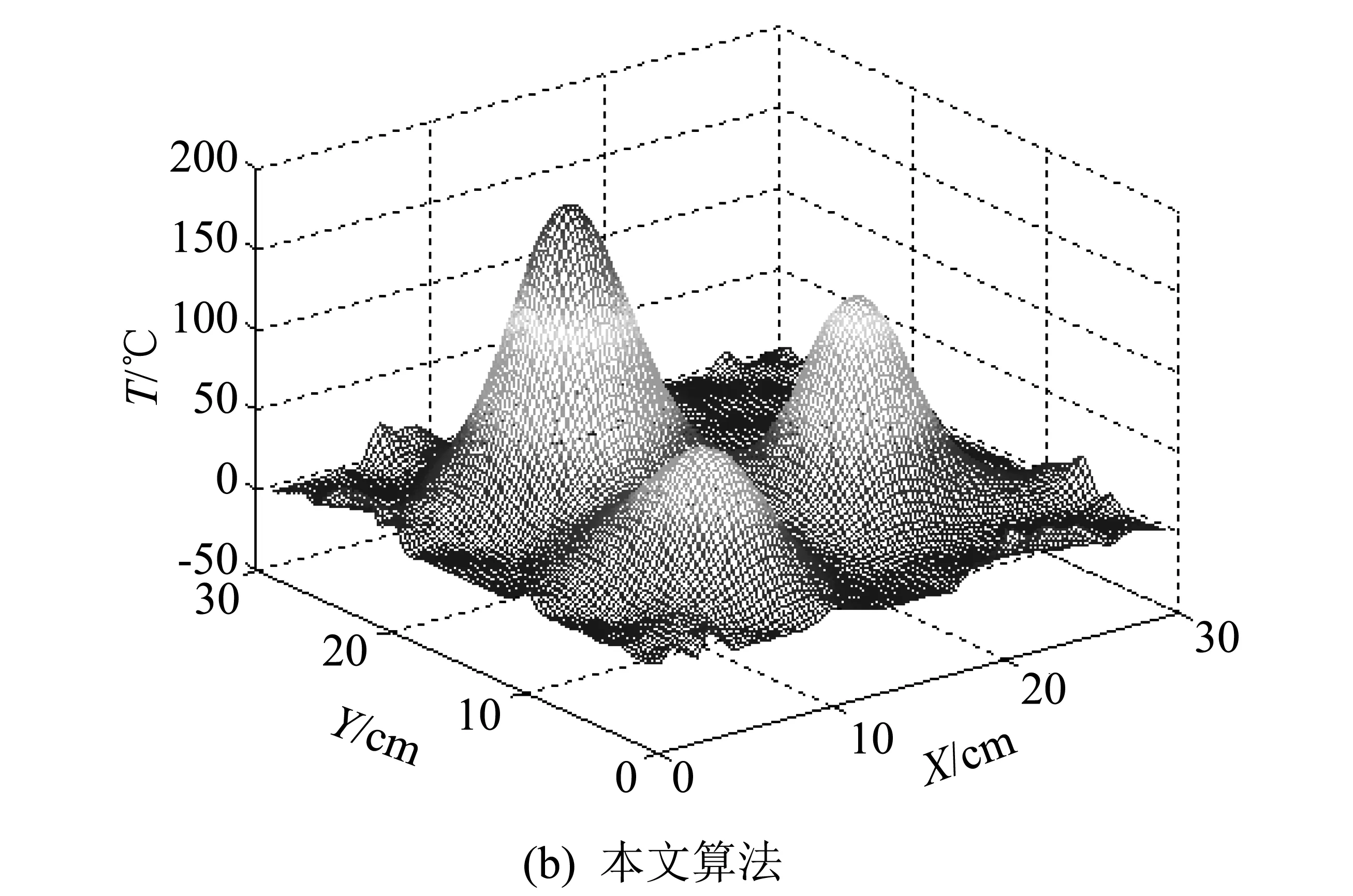

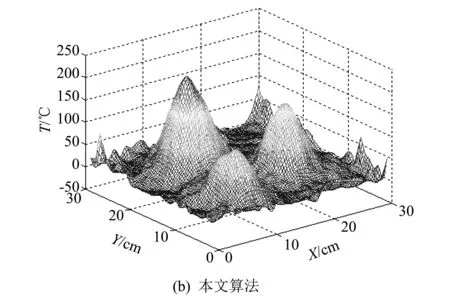

2.3 液化石油气火焰温度场的重建


3 结 论

