表面形貌对流体动压润滑和摩擦的影响

董 磊， 张晓宇， 王俊元， 杜文华， 刘 峰， 石瑞敏

(1. 中北大学 机械工程学院， 山西 太原 030051； 2. 合肥工业大学 摩擦学研究所， 安徽 合肥 230009)

0 引 言

表面形貌对接触界面摩擦和润滑的影响是十分显著的[1]， 其不仅反映表面质量， 而且包含大量的制造与功能信息， 具有保证产品质量和功能的双重作用[2]. 表面形貌表征是设计、 制造表面的前提， 是表面质量和界面功能保证的研究基础.

三维表面形貌的表征方法一般有基准参数法、 Motif法、 分形法、 分水岭法、 小波法等. 这些方法均由二维表面形貌参数表征方法发展而来， 在表面形貌研究中起着重要的作用[3-4]. 但是， 以往的表面形貌相关表征研究还存在着诸如参数过多、 与宏观功能性描述脱节等问题， 仍需要继续针对面向功能的表面表征. Pradeep L Menezes[5-7]发现接触界面摩擦系数与粗糙度参数并没有直接明确的相互关系， 另外发现摩擦系数还与其它诸如纹理等特征参数有关[8]. 表面形貌特征除了与摩擦特性有关以外， 还有表面形貌表征参数与润滑特性之间的关系研究， 例如U Engel等人[9]提出的表面形貌功能性表征参数： 开放空体区参数和封闭空体区参数， 前者能够描述接触界面流体在外载荷作用下流出界面而产生的流体动压力， 后者能够描述接触界面流体在外载荷的作用下被封闭在波“谷”处而形成的流体静压力,两者所对应的参数显示了表面存储和输送润滑剂的能力， 这些参数均对表面的润滑特性产生重要影响.

雷诺方程作为求解流体动压润滑最基本的方程之一， 是Navier-Stokes方程(简称N-S方程)的特殊形式， 雷诺方程的求解相对较为容易， 虽然增加了边界条件和假设等约束， 但依然能够满足一些特殊场合的动压润滑求解要求， 其计算精度在一般工况下能够满足使用要求， 也得到了更为广泛的使用. Feldman等[10]研究了雷诺方程在气体润滑变形平行表面的流体静力效应模型的应用， 通过精确的N-S方程的数值解和雷诺方程的近似解， 得到了单个三维微孔的承载能力和压力分布. 尽管在局部压力上存在较大的差异， 但在实际几何参数和物理参数上， 两种方法在承载能力上的差异很小. Kraker等[11]用Navier-Stokes方程研究了单曲面的局部流动效应, 并与传统的雷诺计算进行了比较， 进一步指出当油膜厚度远小于粗糙接触表面高度幅值时， 采用Half-Sommerfeld边界条件的雷诺方程就可得到较为精确的压力分布， 而不必采用需要更严格约束条件的N-S方程.

雷诺方程是非线性偏微分方程， 只有少数特殊情况下可以得到精确解析解[12-13]. 而实际工况下， 机械接触界面均是随机粗糙接触界面， 接触界面间的流体流动与表面形貌特征密切相关， 表面形貌特征众多， 难以确定表面形貌具体特征与流体在接触界面微流动状态之间的关系， 导致流体在微通道中的流动分析较为困难. 目前， 影响流体微流动的影响因素主要有： 尺度效应、 表面形貌、 流体特性等[14-15]. 其中表面形貌特征对粗糙接触界面流体微流动状态有着不可忽视的影响. 综合上述文献可知， 目前的研究内容主要集中在表面粗糙度参数对规则通道内流体微流动和微通道结构形式上[16-17]. 然而随机粗糙接触界面是一个非线性系统， 表面形貌参数也不止粗糙度一个参数. 因此， 研究随机粗糙接触界面的流体动压载荷和摩擦力以及表面形貌参数对其的影响， 是十分必要且具有一定意义的.

1 雷诺方程及其求解

雷诺方程适用于狭小间隙中的流体黏性流动， 流体需为牛顿流体， 能够描述三维空间内的压力分布和预测摩擦力分布情况等. 它的基本形式为

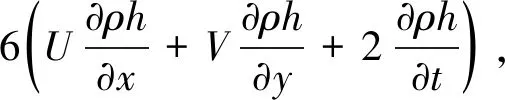
(1)

式中：ρ为液体密度；η为润滑油粘度；h为油膜厚度；p为油膜压力；U为摩擦副相对运动速度；t为时间.

如果相互接触的两个表面相对切向速度不随切向方向的变化而变化， 并且接触材料在运动过程中不发生伸缩效应， 雷诺方程可以简化为

(2)

如式(2)所示， 雷诺方程是一种典型的偏微分方程， 对于求解偏微分方程的有效方法之一即是数值方法. 数值方法中求解偏微分方程的一种较为简单的方法即是有限差分法. 有限差分法求解雷诺方程在很多文献中均有详细说明， 这里不作过多说明， 仅列出最后采用有限差分法求解雷诺方程的基本公式为

φi,j=CNφi,j+1+CSφi,j-1+CEφi+1,j+

CWφi-1,j+G,

(3)

式中

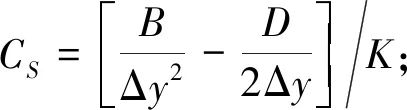
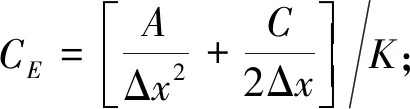
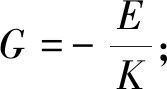
其中，A,B,C,D,E均为已知系数. 通过有限差分法可以获得与未知量数量一致的线性代数方程， 再通过迭代运算， 最终获得网格所有节点的变量值， 这一过程可以利用计算机完成.

2 理论模型

2.1 表面形貌特征函数

雷诺方程中没有包含表面形貌的相关信息， 因为在应用雷诺方程的一般场合中， 表面形貌的特征尺度比相对宏观的楔形间隙小得多. 但如果粗糙接触表面间隙尺寸与表面形貌高度尺寸在相同或相近的尺度范围内， 则必须考虑表面形貌对接触中载荷分布和剪切力等的影响.

在雷诺方程中，h(x,y)表示楔形间隙的特征， 本文通过引入表面形貌特征函数， 将表面形貌特征函数与膜厚方程相结合， 探讨表面形貌特征对雷诺方程计算结果的影响， 求解粗糙接触表面载荷和摩擦力， 最终获得表面形貌特征参数对表面载荷和摩擦力的分布状态的影响.

2.2 膜厚方程

由于考虑了表面形貌对雷诺方程的影响， 则在粗糙接触界面中更多的从面接触、 线接触过渡到了点接触. 由于点接触时载荷的幅值要比面接触或线接触大， 因此本文采用点接触形式. 点接触的膜厚方程可以表示为

(4)

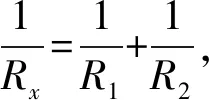
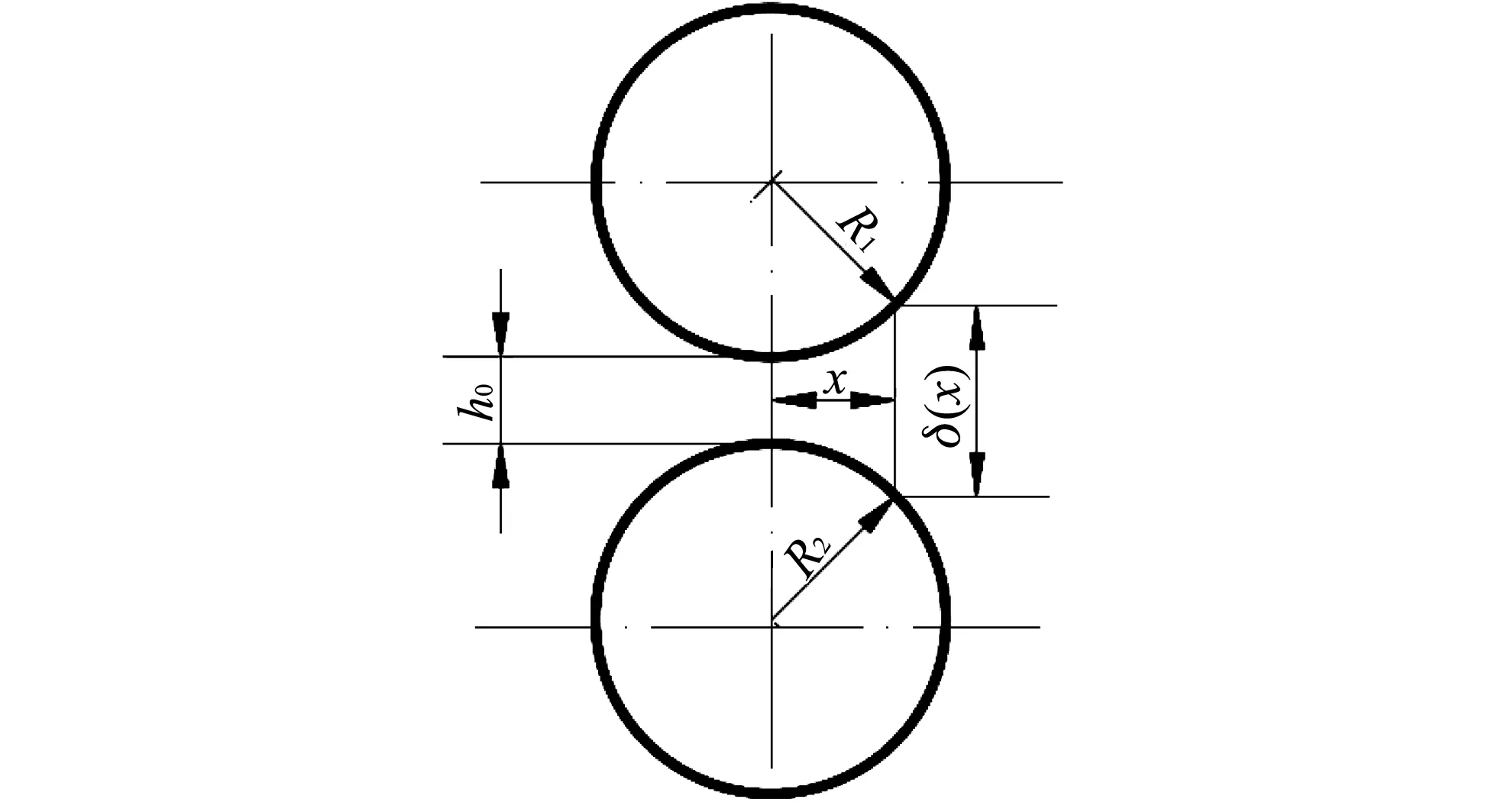
图 1 膜厚方程示意图Fig.1 Schematic diagram of the film thickness equation

2.3 剪切力(摩擦力)方程

如果能够对雷诺方程求得的载荷在接触区域内进行积分， 则可以获得接触范围内的剪切力， 也即摩擦力， 表示为式(5). 此外， 也可以对局部积分区域进行有限差分网格的划分， 能够得到局部摩擦力.

Ff=∬τdxdy=

(5)

采用有限差分法应用MATLAB软件求解三维粗糙接触界面雷诺方程载荷及摩擦力的流程如图 2 所示.

图 2 计算流程图Fig.2 Calculation flow chart

2.4 模型验证

为了了解真实表面的受力情况， 依据文献[18]随机粗糙表面的建模方法建立不同形貌参数的随机粗糙表面如图 3 所示， 通过对雷诺方程求解和摩擦力计算得到了部分模拟表面的载荷分布以及摩擦力分布图， 经仿真对比可得近似的载荷分布趋势. 如图 4 所示为随机粗糙三维接触界面的载荷分布状态图， 图 5 所示为随机粗糙三维接触界面的摩擦力分布状态图.

图 3 三维随机粗糙表面Fig.3 Three-dimensional random rough surface

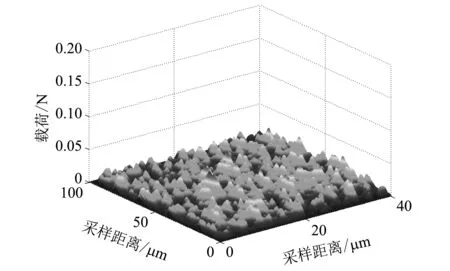
图 4 三维随机表面载荷分布Fig.4 Loads distribution of three dimensions random surface

图 5 三维随机表面摩擦力分布Fig.5 Friction forces distribution of three dimensions random surface

由此可知， 载荷分布和摩擦力分布与随机粗糙表面的表面形貌呈现出吻合的状态， 载荷在随机表面中沿着微凸体方向较为均匀随机的分布， 在波“峰”处载荷较大， 在波“谷”处载荷较小. 摩擦力分布则呈现出与运动方向相关并且相对滞后的分布趋势， 仿真结果与相关文献和相关实验的结果一致.

3 表面形貌特征参数对流体动压载荷和摩擦力的影响

定量分析表面形貌参数对流体动压载荷和摩擦力的作用机理十分必要的. 由于表面形貌参数数量较多， 这里只针对部分能够描述表面特征的几个重要参数进行讨论， 其余参数可以类比得到. 为对比表面形貌参数对接触载荷和摩擦力的影响， 本小节所得结论均在相同边界条件下重复三次实验后获得， 如初始压力(1 MPa)和初始边界速度(1 mm/s)等.

1) 表面高度均方根偏差Sq表示在表面采样范围内表面形貌各点高度幅值的均方根值， 是描述粗糙表面在高度方向上的重要参数之一, 其定义为

(6)

式中：z(x,y)为表面上各采样点的高度幅值；lx,ly为采样区域的边界长度；M，N分别为采样范围内沿X方向和沿Y方向上的采样点数.

图 6 所示为表面最大载荷和最大摩擦力随表面高度均方根偏差Sq的变化趋势， 由图可以看出， 随着表面高度均方根偏差Sq的增大， 动压载荷和摩擦力都呈非线性显著增大的趋势， 表面载荷和摩擦力对表面高度均方根偏差Sq的敏感度较高， 这是因为表面高度幅值越大， 表面越粗糙， 形成的油楔深度越深， 载荷和摩擦力增长速度越快， 摩擦系数也随之升高.

2) 表面高度分布偏态Ssk表示表面上各采样点的高度幅值相对于基准平面的距离偏差， 是衡量粗糙表面“峰”、 “谷”特征的参数之一， 其定义为

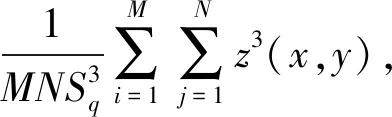
(7)

式中：S表示采样面积；P(z)表示采样区域内各采样点高度幅值分布函数z(x,y)的概率密度函数.

图 6 载荷和摩擦力与Sq的关系Fig.6 Relation between load and friction force and Sq

图 7 所示为表面最大载荷和最大摩擦力随表面高度分布偏态Ssk的变化趋势， 由图可以看出， 随着表面高度分布偏态Ssk绝对值的增大， 动压载荷和摩擦力都呈非线性增大， 但摩擦力较载荷的变化幅度小， 表明摩擦系数对表面高度分布峰态的变化较不敏感. 表面高度分布偏态主要衡量的是表面是以“峰”特征为主还是以“谷”特征为主， 以“峰”特征为主的表面所受载荷较大， 以“谷”特征为主的表面可以更多地存储流体， 载荷和摩擦力较小， 但随着“谷”的深度增加， 载荷也会因为油楔深度过深而随之增加.

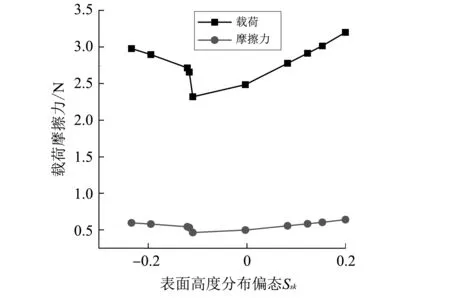
图 7 载荷和摩擦力与Ssk的关系Fig.7 Relation between load and friction force and Ssk

3) 自相关最快衰减率Sal表示标准自相关函数沿在某个方向上衰减最快的距离， 是描述表面粗糙度频率的主要参数， 其定义为

(8)

式中：τx,τy表示采样区域内各采样点高度幅值沿X或Y方向的衰减率.

图 8 所示为自相关最快衰减率Sal与表面最大载荷和最大摩擦力的关系， 由此可以看出， 随着自相关最快衰减率Sal的增大， 最大载荷和摩擦力都显著非线性减小， 表明表面“峰”、 “谷”出现的频率越低， 表面最大载荷和摩擦力越小. 但摩擦力对自相关最快衰减率Sal比对表面高度均方根偏差Sq的敏感度较低， 说明摩擦系数随自相关最快衰减率Sal的变化较小.

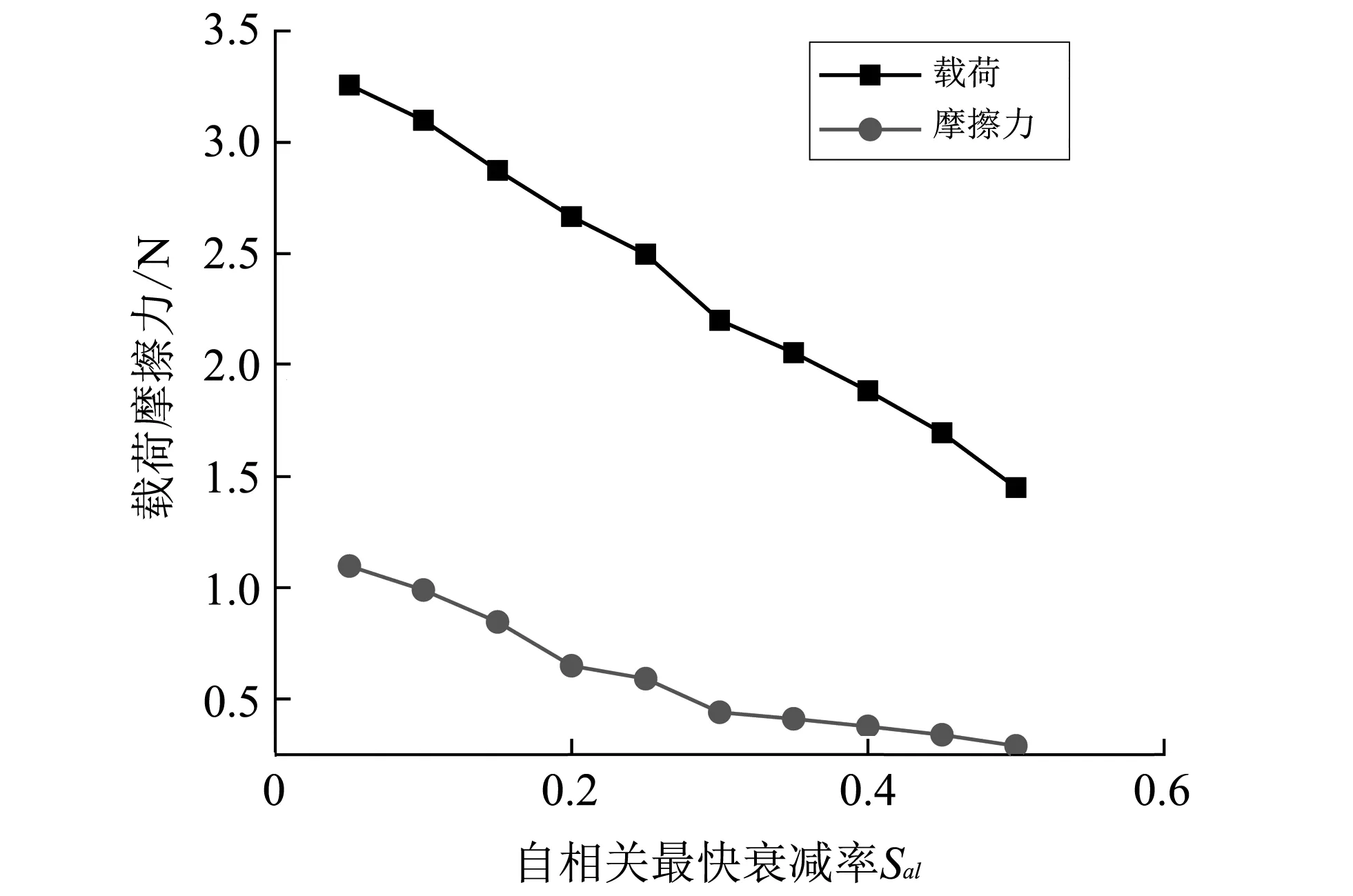
图 8 载荷和摩擦力与Sal的关系Fig.8 Relation between load and friction force and Sal

4) 表面展开面积比Sdr表示被测表面采样范围内表面面积的增量与采样范围面积的比率， 是描述表面纹理特征的一个参数， 其定义为

(9)

其中

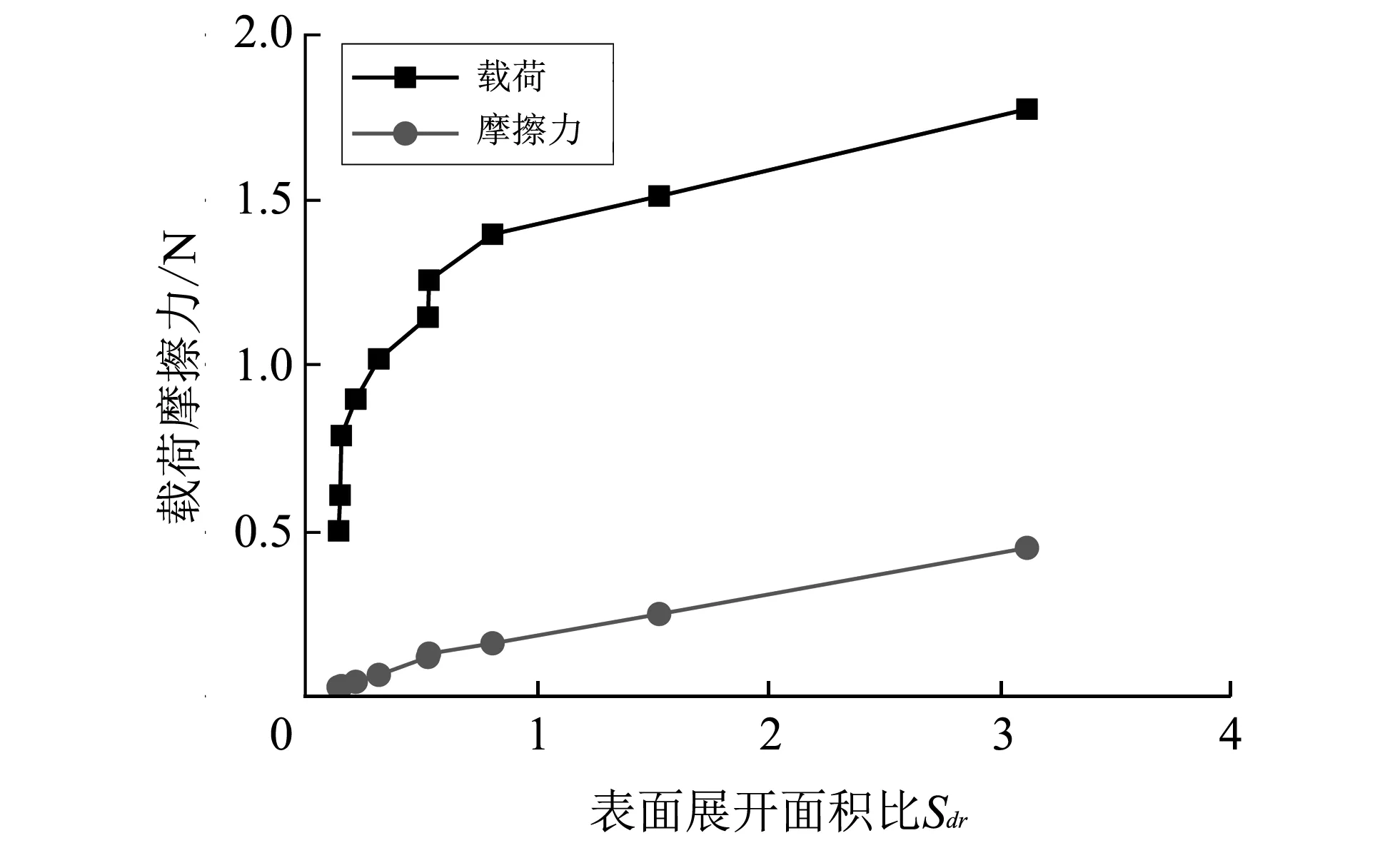
图 9 载荷和摩擦力与Sdr的关系Fig.9 Relation between load and friction force and Sdr

图 9 所示为表面最大载荷和最大摩擦力随表面展开面积比Sdr的变化趋势， 由图可以看出， 随着表面展开面积比Sdr的增大， 最大载荷和摩擦力均呈非线性增大的趋势， 与自相关最快衰减率Sal类似， 摩擦系数对表面展开面积比Sdr的敏感度较小.

4 结 论

为了获得表面形貌表征参数对粗糙接触界面摩擦和润滑的影响， 本文基于雷诺方程及其有限差分法求解理论建立了随机粗糙界面的计算方法， 然后通过计算机模拟随机表面， 对模型和计算方法进行了仿真验证.

表面形貌表征参数对粗糙接触界面摩擦和润滑的影响在许多研究文献中都有一定的阐述， 本文选取了四个ISO 25178表面形貌国际标准特征参数： 表面高度均方根偏差Sq、 表面高度分布偏态Ssk、 自相关最快衰减率Sal和表面展开面积比Sdr， 探讨了表面形貌特征参数对粗糙接触界面载荷和摩擦力的影响， 研究结果可以进一步补充现有的流体动压润滑和表面形貌表征等相关研究内容.