基于投影域分解的多能谱CT造影剂物质识别研究

孙英博， 孔慧华， 张雁霞

(1. 中北大学 理学院， 山西 太原 030051； 2. 中北大学 信息探测与处理山西省重点实验室， 山西 太原 030051)

0 引 言

近年来， 随着光子计数探测器和 CT 制造技术的发展[1-4]， 多能谱CT成像技术日益成熟， 在对小病灶的定性定量诊断、 减少高危患者造影剂使用量等方面有突出贡献. 双能 CT作为多能谱CT的一种， 不仅可以确定尿结石是否含有钙， 还可以区分钙、 骨与碘造影剂， 并提供一系列CT组织表征[5-9]. 但双能CT仅限于两种能量， 提供的能谱信息有限导致采集到的物质衰减信息有限， 重建图像中物质区分度不高. 为了更充分地使用材料的多能量衰减特性， 增加能量通道数量以获得更丰富的投影信息， 对CT成像技术有重要意义.

基于光子计数探测器的多能谱CT可以在一次扫描中得到物体在多个能区下的成像结果， 利用材料的能谱特性将材料间的差异最大化进而实现对材料的识别， A.P.Butler[10]等开发了一种基于Medipix2光子计数检测器的多能谱CT(MARS)， 应用光谱CT区分具有不同K-edge的造影剂； Daniel Y. Chong等[11]和J P Schlomka等[12]分别通过实验对双能CT中造影剂的可分离性及多能CT光子计数K-edge成像在临床实验中应用的可行性进行了评估. 对于物质识别重建算法的研究， 投影域分解具有重要的应用价值， 现有文献中已有多种投影分解方法. Alvarez和Macovski等[13]提出了基于双能CT的基物质分解模型和基效应分解模型； 吴笃蕃[14]通过实验针对双能CT双物质分解及三物质分解进行了研究； Bernhard Brendel[15]等在双物质分解模型的基础上引入第三基础成分,在将测量的投影数据分解成基础分量投影之后， 执行传统的滤波反投影重建获得基础分量图像， 实现了对造影剂物质的识别.

本文对多能谱CT造影剂物质识别进行研究， 在双效应分解模型的基础上增加与待识别造影剂物质K-edge相关的基函数， 应用最小二乘法对不同能量通道下所获得的待测物体的投影信息进行分解， 再通过传统的反投影重建算法获得康普顿效应、 光电效应及各造影剂物质所对应的重建图像， 最后对各造影剂物质对应的重建图像衰减值进行分析实现各造影剂物质的分离成像、 定量表示及彩色表征.

1 基效应分解模型

多能谱CT应用光子计数探测器设置阈值范围， 将衰减后的光子能量分能区进行计算， 得到物体在不同能量通道下的投影， 各能量通道中成像原理与传统CT相同. 因此， 在多能谱 CT 中， 各能量通道下X 射线穿过物质的衰减可以表达为该能量通道中不同能量下衰减的加权平均， 即

(1)

式中：EBin为当前能量通道；I0和I分别为当前能量通道下入射X射线的初始光子数及最终探测器接收到的光子数；S(E)是当前能量通道下光子的等效能谱；μ(E,x)是物质的线性衰减系数随能量E和位置x的分布， 也就是成像需要求解的量； 积分路径l表示这条射线在物体中所穿过的路径.

由式(1)可得， 当前能量通道EBin中， 投影函数为

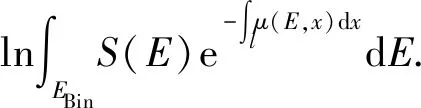
(2)

直接求解μ(E,x)未知数太多， 通常需要对它加以一定的假设， 即假设物质的衰减系数可以展开成I个基函数[12]

(3)

式中：fi(E)是给定的基函数；bi是组合系数[14].

常用的衰减系数模型有两种[10]： 基物质分解模型和双效应(光电效应、 康普顿散射效应)分解模型. 常见的 “双效应分解”模型为

μ(E)≈apfph(E)+akfKN(E),

(4)

式中：fph(E)是光电效应截面对能量的依赖关系.

(5)

式中：fKN(E)是 Klein-Nishina 函数， 表达了康普顿截面对能量的依赖关系.

(6)

式中：α=E/510.975 keV.

当X射线的能量增大到原子K层电子的束缚能之上时， 射线可以与K层电子发生作用， 导致光电吸收截面突然增大产生K-edge效应. 原子序数越高， K 层电子的束缚越大， K-edge对应能量也会越高. 当待识别物质 K-edge 对应能量足够高时， 在衰减系数空间中产生一个新的基函数[8,14]， 此时双效应分解模型可进一步写成

μ(E,x)≈apfph(E)+akfKN(E)+

(7)

式中：N是K-edge 物质的种类，μn(E,x)是第n种物质对应的线性衰减系数.

为方便计算， 记：ap=b1;ak=b2;an=bn+2，fph(E)=f1(E);fKN(E)=f2(E);μn(E,x)=fn+2(E)(n=1,2,…,N)， 将式(7)写为式(3)的形式

(8)

2 基于最小二乘法的投影域分解

本文基于光子计数探测器， 对能谱CT投影的特性进行研究， 进而寻找投影分解的方法. 设所选M个能谱通道分别为EBin1,EBin2,EBinM， 各能量通道下的投影分别为P1,P2,…,PM， 具有K-edge的待识别造影剂物质为N种， 实验中通常取N≤3.

由式(2)， 式(8)可得各能量通道下的投影

(9)

式(9)可进一步写成

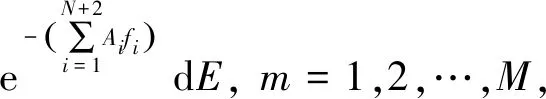
(10)

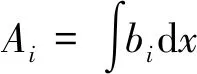
(11)

根据式(5)， 式(6)及能谱信息， 将f1(EBinm),f2(EBinm)(m=1,2,…,M)表示为

m=1,2,…,M,

(12)

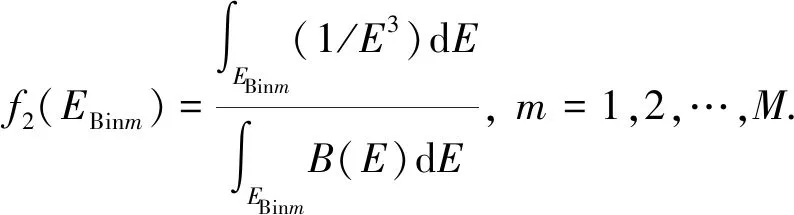
(13)

根据NIST数据库中各造影剂物质的线性衰减系数及能谱信息， 将fi(EBinm)(m=1,2,…,M;i=3,4,…,N+2)表示为

m=1,2,…,M;n=1,2,…,N;i=n+2,

(14)

式中：B(E)为第m个能量通道EBinm(m=1,2,…,M)中各能量下空扫描时探测器所接收到的光子数；CoefaN(E)为第m个能量通道EBinm(m=1,2,…,M)中各能量下第n种物质所对应的衰减系数.

为方便求解， 将式(11)写为针对投影矩阵单个像素的矩阵形式

P=AP*,

(15)

式中：P=[P1(i,j)P2(i,j) …PM(i,j)]T, (i,j)为投影的像素位置，i=1,2,…,I为采集投影的某一视角，I为采集投影的视角总数，j=1,2,…,J为采集投影的射线标号，J为采集投影的射线总条数.

式(14)有M个方程N+2个未知量个数， 为获得更丰富的投影信息， 抑制重建中噪声放大的影响， 通常M>N+2， 即式(14)为超定方程组.

应用最小二乘法解超定方程组有如下定理：x0为超定方程组Ax=b最小二乘解的充分必要条件为x0是ATAx=ATb的解. 由此可得， 式(15)与式(16)同解

ATAP*=ATP.

(16)

对式(16)左右两边同乘(ATA)-1可得

P*=(ATA)-1ATP.

(17)

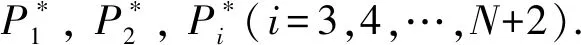
应用FBP重建算法对各分解投影进行重建， 得光电效应、 康普顿效应及各具有K-edge的造影剂物质所对应的重建图.

光电效应和康普顿效应重建图显示物体的内部结构， 各具有K-edge的造影剂物质对应的重建图突出显示各造影剂所在位置， 达到物质识别与区分的目的.

3 仿真实验

碘和钆具有足够高的K-edge， 是医疗CT检测中常用的造影剂物质. 因此， 仿真实验中选用碘和钆元素作为待识别物质. 投影重建算法选用计算较为简单， 运行时间相对较少的FBP重建算法.

3.1 数值仿真模型

仿真模体大小为10 cm×10 cm， 如图 1 所示， 含有 8 个圆孔， 5 种材料， 各材料参数由表 1 列出. 3～8号圆孔外围为厚度0.5 cm的骨物质. 所有材料的衰减系数， 密度等物理参数由 NIST 数据库获取.

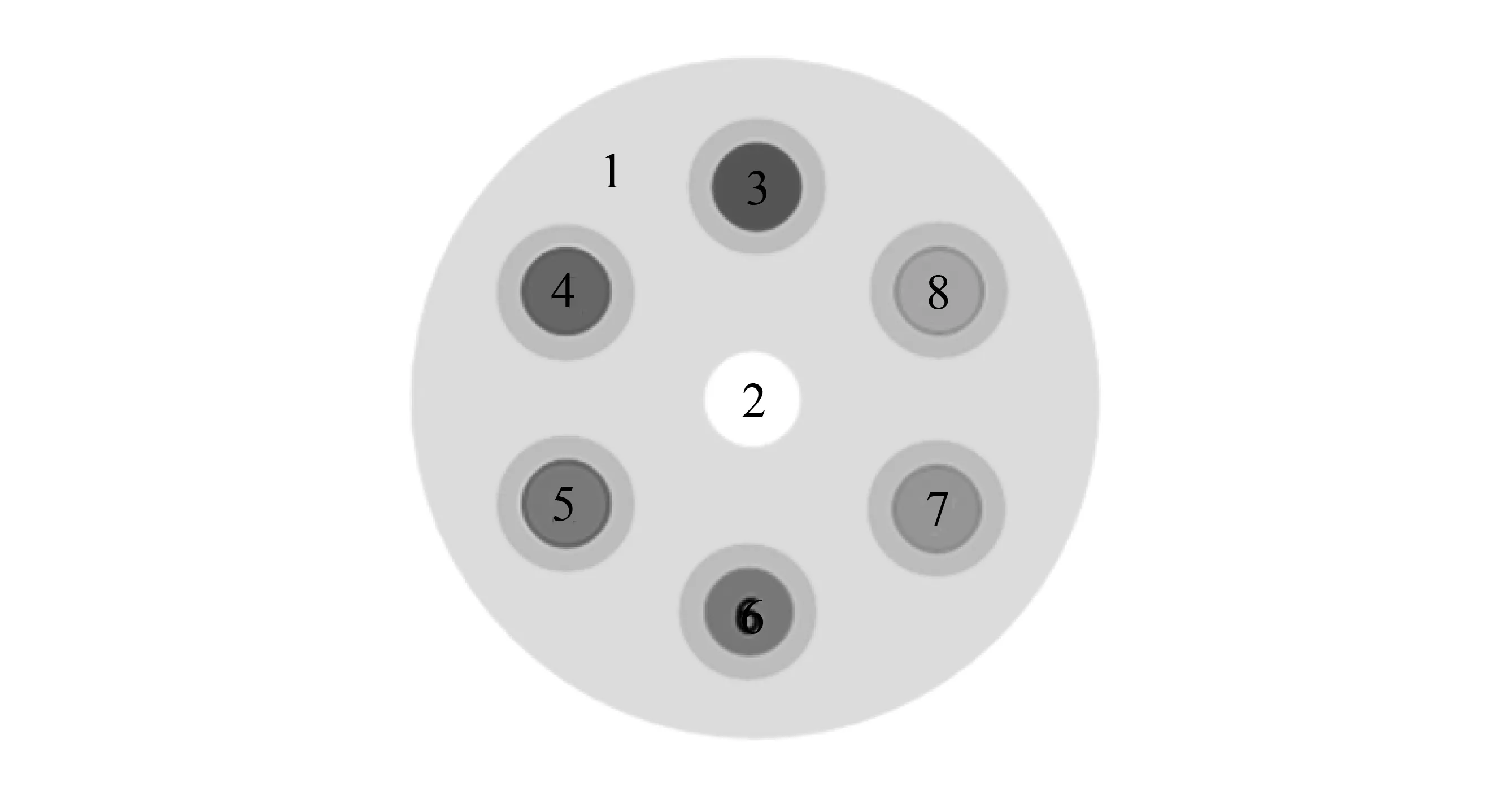
图 1 5种不同材料组成的圆孔模体截面图Fig.1 Cross-sectional view of a circular hole phantom composed of 5 different materials

3.2 数值仿真环境及能谱通道范围

仿真电压采用120 kVp， 以物质K-edge所在能量： 碘 (33 keV)、 钆(50.2 keV)为通道划分界限的参考值， 将能谱区域划分为 6 个能量通道， 在图 2 中用不同颜色表示， 分别为：

EBin1={25～30 keV}；EBin2={30～40 keV}；

EBin3={40～50 keV}；EBin4={50～60 keV}；

EBin5={60～80 keV}；EBin6={80～120 keV}.

仿真实验中采用等距扇束扫描， 模体分辨率为 256×256像素. 探测器为由320 个探元组成的光子技术探测器， 采样角度为360°， 采样间隔为1°.

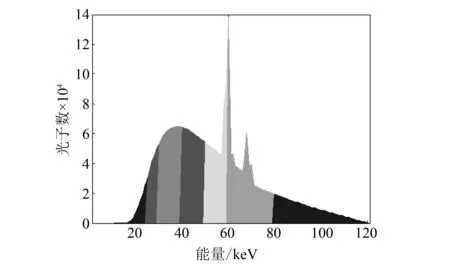
图 2 用于数值模拟源光子发射光谱Fig.2 For numerical simulation of source photon emission spectroscopy

3.3 数值仿真实验与结果

根据式(17)将6个能量通道下所采集的投影进行分解后所得投影见图 3， 图 3(a)～(d)分别对应光电效应、 康普顿效应、 碘图、 钆图的分解投影.

应用FBP算法对图3中分解后所得投影进行重建， 重建图见图 4， 图 4(a)～(d)分别对应光电效应、 康普顿效应、 碘图、 钆图的重建结果.

图 3 6个能量通道下投影分解后所得投影Fig.3 Projection obtained after projection decomposition under 6 energy channels

图 4 分解后投影重建结果Fig.4 Projection reconstruction result after decomposition

由图 4(c) 可见， 3, 4, 5号含钆元素的圆孔较其他位置更亮， 且亮度随钆浓度的降低逐渐降低， 其中3～8号圆孔位置图像衰减值分别为： 0.005 3, 0.004 2, 0.003 6, 0.003 0, 0.003 0, 0.003 0. 由此可见， 钆图中含不同浓度碘元素的圆孔被作为衰减值相同的“背景部分”， 含钆元素的圆孔灰度值随钆浓度的降低而降低且其与“背景部分”灰度值的差与钆浓度成正比例 ， 见表 2.

表 2 图4(c)图像灰度值与钆浓度关系Tab.2 The relationship between image gray value and gadolinium concentration in Fig.4(c)

由图 4(d) 可见， 6, 7, 8号含碘元素的圆孔较其他位置更亮， 且亮度随碘浓度的升高逐渐升高， 其中3～8号圆孔位置图像灰度值分别为： 0.004 0, 0.004 0, 0.004 0, 0.007 1, 0.005 1, 0.005 0. 由此可见， 碘图中含不同浓度钆元素的圆孔被作为灰度值相同的“背景部分”， 含碘元素的圆孔灰度值随碘浓度的升高而升高且其与“背景部分”灰度值的差与碘浓度成正比例 ， 见表 3.

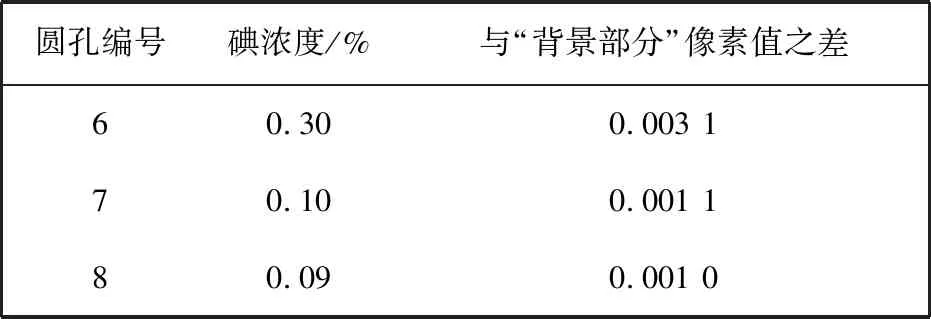
表 3 图4(d)图像灰度值与碘浓度关系Tab.3 The relationship between image gray value and iodine concentration in Fig.4(d)

综上， 实验通过对各材料对应位置灰度值的对比分析实现对造影剂物质浓度的定量分析.

3.4 待识别物质的分离成像及彩色表征

为了更方便清晰地识别仿真模体中的造影剂物质， 将图 4(c), 图4(d)的窗口显示阈值分别调整为[0.003 1,0.005 3]和[0.004 1,0.007 1]实现钆和碘的分离成像， 然后应用RGB颜色通道对分离出的钆和碘进行彩色表征， 如图 5(a)， 图 5(b)， 最后将钆和碘的彩色表征图像与显示仿真模体内部结构的图 4(a), 图 4(b)进行加权融合. 图 5(d)既显示了仿真模体的内部结构， 又实现了对钆和碘元素的识别及颜色表征， 且颜色越深表示浓度越高.

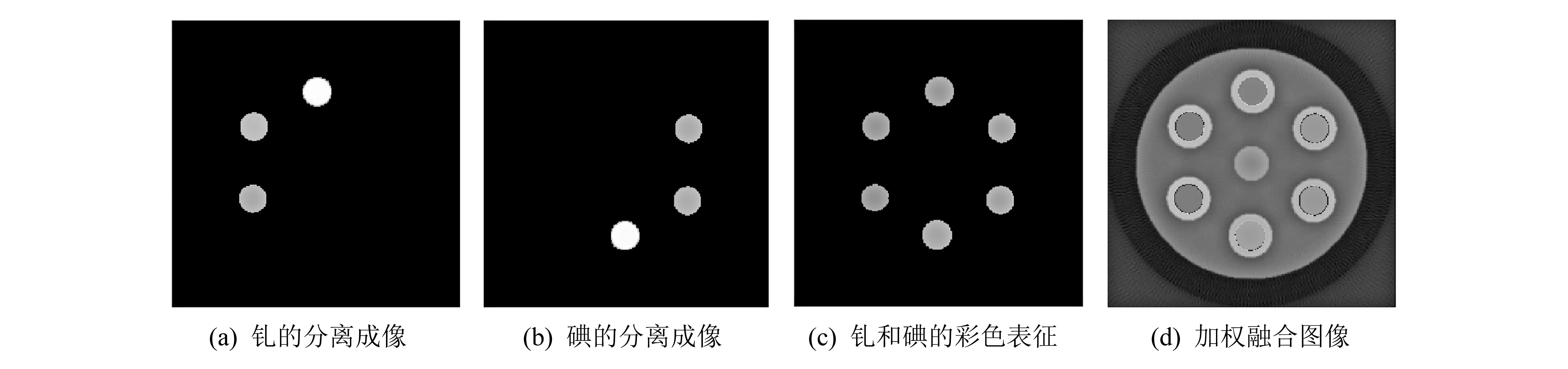
图 5 碘和钆的分离成像与彩色表征Fig.5 Separation imaging and color characterization of iodine and strontium

4 结 论

医疗CT成像中造影剂物质的识别及定量分析有助于研究物体中造影剂物质的分布及其累积程度， 对病灶诊断、 降低辐射剂量等问题的研究有重要意义. 目前基于前处理的投影域分解方法可通过基物质分解或基效应分解实现对两种或三种造影剂物质的识别. 本文基于光子计数探测器， 推导了能谱CT投影基效应分解模型， 应用最小二乘法对多个能谱通道下的投影进行分解和重建， 达到了造影剂物质识别与定量分析的目的. 由于光子计数探测器可以同时获取多个能量通道的投影， 从而可以实现多个基物质的分解， 为能谱CT物质识别提供有效支持.