一种基于样本近邻分类精度的支持向量机集成方法

吕晓燕， 陈立潮

(1. 山西医科大学 计算机教学部， 山西 太原 030001； 2. 太原科技大学 计算机科学与技术学院， 山西 太原 030024)

0 引 言

随着数据以及大数据价值的不断发现， 机器学习、 深度学习方法被越来越多地应用于数据处理. 其中， Support Vector Machine(SVM)， 即支持向量机方法， 更是备受推崇[1-3]. 已有的研究表明： 集合多个SVM分类器， 可以提高系统的泛化能力[4-6]. Zhou[3]等人在研究中进一步发现， 选择部分SVM分类器集成， 性能要优于使用所有个体SVM分类器. 文献[4]构建了二级SVM分类器， 利用投票法集成. 文献[6]提出了多级支持向量机. 文献[7]将灰色理论引入SVM的集成， 进行预测等. 这些研究为SVM的集成学习提供了新的思路[8-10]. 但实际应用中， 分类器常常需要随着新样本的特征， 能自动调整， 以增加自适应性.

基于此， 本文提出一种自适应支持向量机集成方法. 通过对待定样本的特征分析, 利用算法在样本空间搜索其近邻. 在此基础上， 依据各个SVM分类器在近邻的分类精度,择优挑选部分SVM组合. 集成过程中， 无论是分类器成员还是分类器在集成中所占的权重， 都能随着待判别样本的特征自动调整， 实现了“私人定制”.

近邻如何确定， 分类器如何选取， 集成时各分类器占的权重如何确定， 是本文重点阐述的内容.

1 基于待定样本的近邻搜索

在模式特征空间划分中， 待定样本的近邻， 是指与之特征相近的一组训练样本. 如何获取近邻是本研究解决的首要问题.

1.1 相关理论

1.1.1 模糊C均值聚类(FCM)

设X={X1,X2,…,Xn}∈R, 为样本空间的数据集， 将样本集划分为C类,V={V1,V2,… ,Vc}为C个聚类中心. FCM的义目标函数为

(1)

约束于

∀j=1,…,n,

式中：U为隶属度矩阵；uij为隶属度.

注意到， 式(1)的目标函数中， 默认样本的各个特征对分类所起的作用相同， 有悖实际情况. 因此， 对式(1)进行修正， 修正后的目标函数为

(2)

式中：wk为样本各属性的权重.

1.1.2 模糊贴近度

设A和B是论域X={x1,x2,…,xn}上的两个模糊集合，μA(x)，μB(x)为隶属度函数. 则A,B的海明加权相对距离为

(3)

式中：w(xi)为权重， 满足

1.2 基于样本特征的近邻搜索

为了确定待分类样本的近邻， 基于改进的FCM及模糊贴近度的近邻搜索算法， 在MATLAB环境下， 完成程序的设计.

首先， 通过改进后的FCM算法， 将样本特征空间：X={X1,X2,…,Xn}划分为c个模式特征空间：A1,A2,…,Ac， 聚类中心分别为V1,V2,…,Vc.

然后， 根据待分类样本B的特征， 据式(3)， 计算B与各类的模糊贴近度.

若δ(Vi,B)=max{δ(V1,B),δ(V2,B),…,δ(Vc,B)}, 则B最贴近Vi.

则Vi所在的模式特征空间上所有的样本均为待定样本B在特征空间上的近邻.

基于改进的FCM与模糊贴近度的样本近邻搜索算法如下：

Step 1 初始化： 样本分类数为c(2≤c≤n)， 误差精度为ξ,U(0)为初始矩阵.

Step 2 计算各聚类中心Vi(i=1,2，…，c)

(4)

其中

i=1,2,…,c;j=1,2,…,n.

(5)

Step 3 修正划分矩阵U(l)

(6)

Step 4 比较U(l)与U(l+1). 对取定的ξ>0， 若‖U(l+1)-U(l)‖≤ξ, 则迭代停止， 转step 6. 否则，l=l+1， 转step 2继续迭代.

Step 5 据式(3), 计算待分类样本与各个类的模糊贴近度， 最大值所在的类为其归属类.

Step 6 结束.

2 基于样本近邻分类精度的SVM集成

2.1 基于近邻分类精度的分类器选择

依据样本近邻的分类， 构造混淆矩阵如式(7)所示.

(7)

设N为类别数， 定义分类精度

(8)

式中：rjj为分类器能正确分类的样本数；rjl为误将j类的样本错分到l类的样本数.

由于样本特征变化会影响SVM分类器的分类能力， 因此， 对待分类样本确定以下分类器选取原则： 依据各分类器在其近邻的分类精度值， 从高到低择优选取. 对于某个分类器SVMi， 当其分类精度LAi大于精度阀值λ时， 该分类器被选择集成.

2.2 基于样本近邻分类精度的分类器集成

假设有k个分类器被选中. 对于每个被选中的分类器， 设其在待分类样本近邻的分类精度为LAi， 则该分类器在集成时， 权重wi可用式(9)计算.

(9)

集成判决模型为

(10)

基于样本分类精度的SVM集成算法， 部分代码如下：

Fork=1 toK

利用混乱矩阵CM计算LALk(x)；

Do procedure_select()； 选择l个分类器

Fork=1 tol

计算SVMk(x);

If 所有的SVMk都把x判给相同的类别

Thenx就属于该类别

Else

End for

Procedure_ select()： 选择过程:

Fork=1 toK

IfLAk(x)≥λ；λ为阈值

Then 第k个分类器被选中

Else

Goto 返回循环起始语句， 继续循环

Endfor

集成判决流程图如图 1 所示.

图 1 SVM集成方法流程图Fig.1 Flowchart for support vector machine integration

3 实验结果及分析

3.1 数据集与实验环境

选取UCI标准数据集中的2个医学数据集Cardiotocography和 Liver disorder数据集， 在Matlab环境下， 进行数据的分类及预测. 数据集信息如表 1 所示.

表 1 数据集信息Tab.1 Data set information

3.2 数据的预处理及特征提取

为了提取对分类有影响的重要指标， 在对数据归一处理的基础上， 利用Relief算法， 对两个数据集， 提取重要的特征指标， 并赋予相应的权重. 结果如表 2 和表 3.

表 2 Cardiotocography数据集属性及权重Tab.2 Cardiotocography data set

表 3 Liver disorder数据集属性及权重Tab.3 Liver disorder data set

3.3 集成分类器成员的选择

利用Bagging技术， 训练产生100个SVM分类器. 选用径向基核函数， 设置参数为：σ2=0.06，C=10.

调整精度阈值λ， 可改变集成分类器的组合规模. 根据不同的λ取值， 分别确定不同数目的分类器组合， 观察对分类结果的影响. 结果如图 2 和图 3 所示.

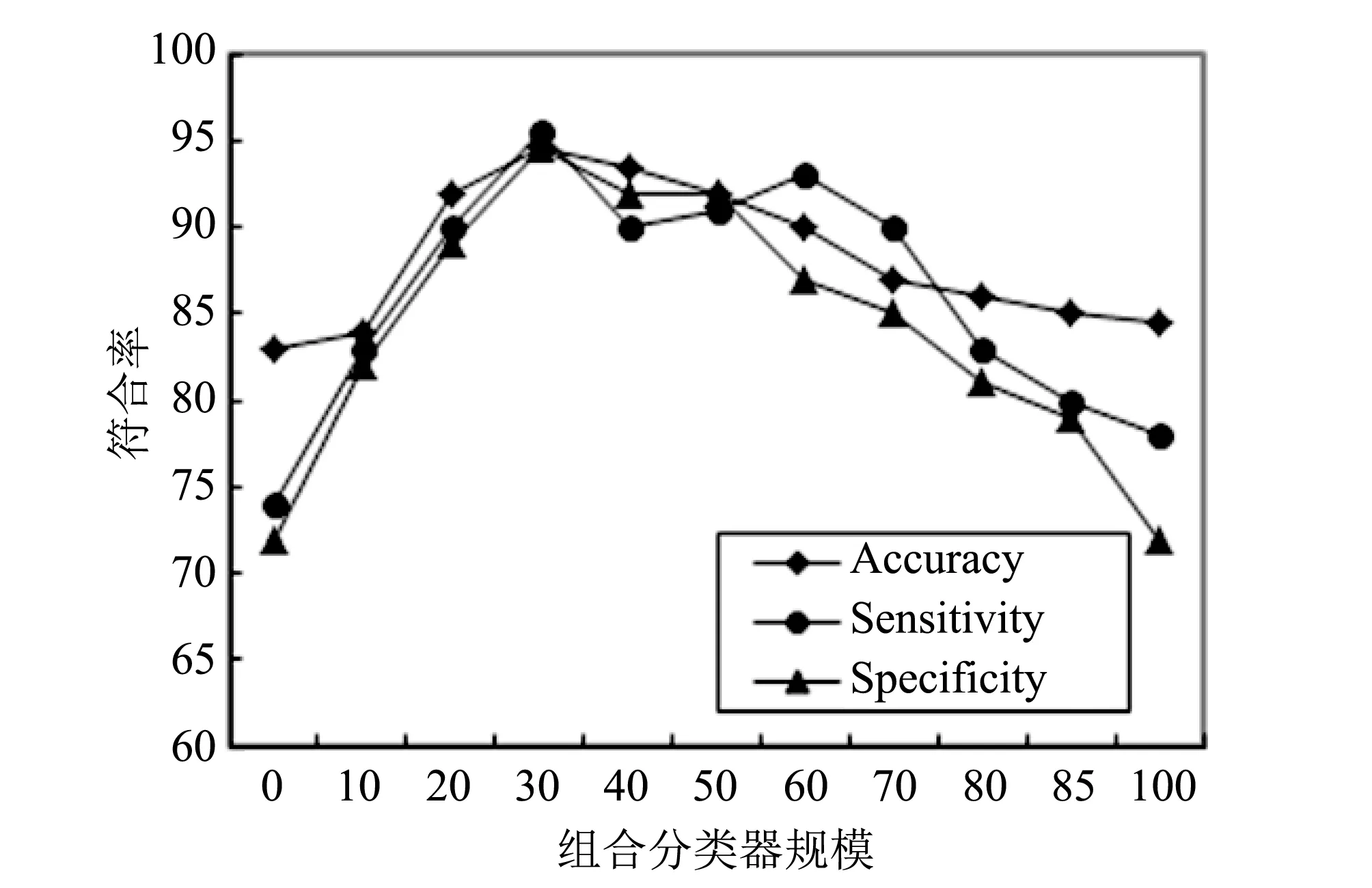
图 2 λ取不同值在Cardiotocography上的分类结果Fig.2 Results on cardiotocography

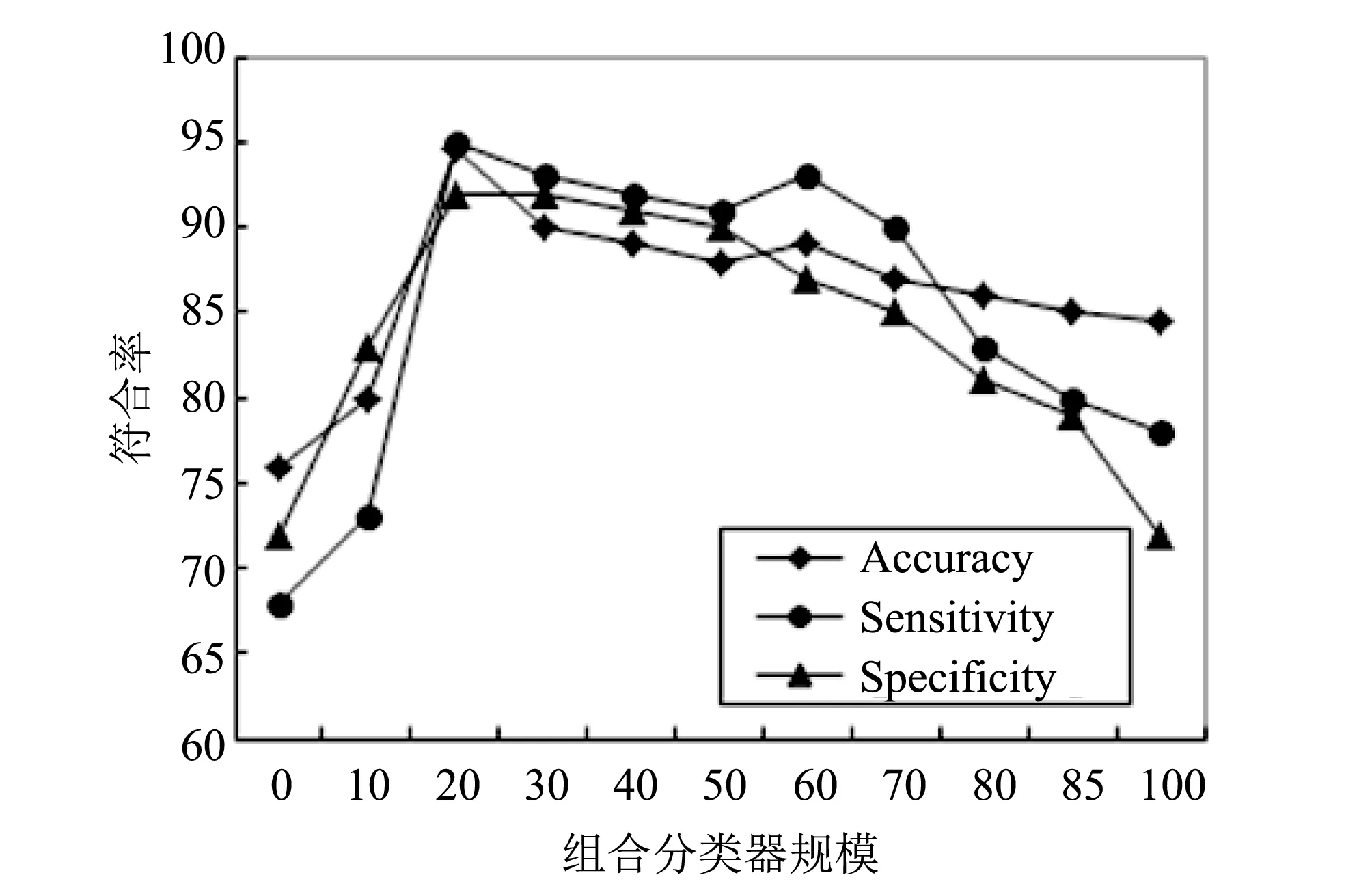
图 3 λ取不同值在Liver disorder上的分类Fig.3 Results on liver disorder

图 2 和图 3 显示， 随着集成中分类器个数的增加， 准确率开始上升， 直至最高. 此时， 图 2 对应的分类器个数为26(λ为0.527)， 图3对应的分类器个数为21(λ为0.431). 继续增加分类器个数， 发现准确率反而下降， 说明集成中选择的分类器并非越多越好. 实践中， 可以通过不断调整精度阀值λ的值， 以获得最佳的组合分类器个数.

3.4 不同集成方法分类结果的比较

将本文方法构建的分类器与其它分类器从分类性能方面比较， 结果如表 4 所示.

其中， Bagging和Boosting集成， 采用的算法分别为RF(Random Forest)算法和Adaboost算法.

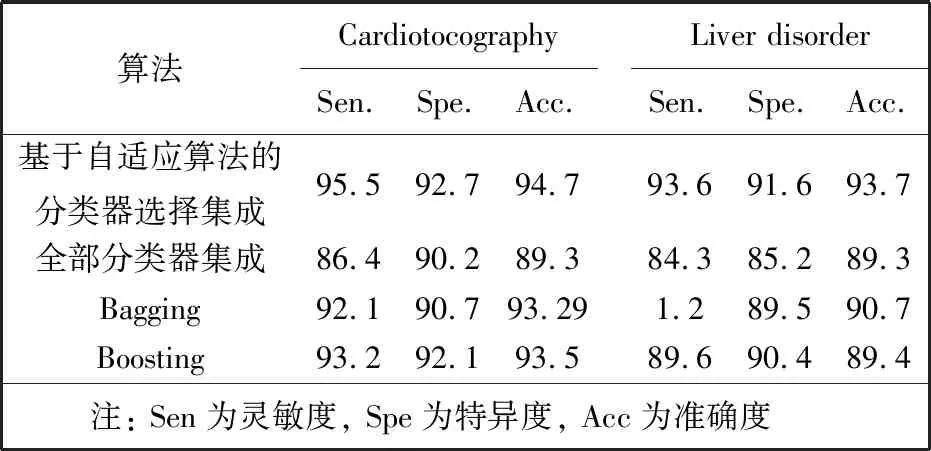
表 4 几种方法的分类结果Tab.4 Classification results of several methods

表 4 显示， 本文方法构建的分类器与其它常见的分类器相比， 无论是准确度， 还是灵敏度或者或特异度， 都有明显的优势. RF算法与Adaboost算法分类， 分类效果接近， 均高于全部分类器集成.

进一步在两个数据集的测试集上比较几种集成分类器的判决时间， 结果如图 4 所示.

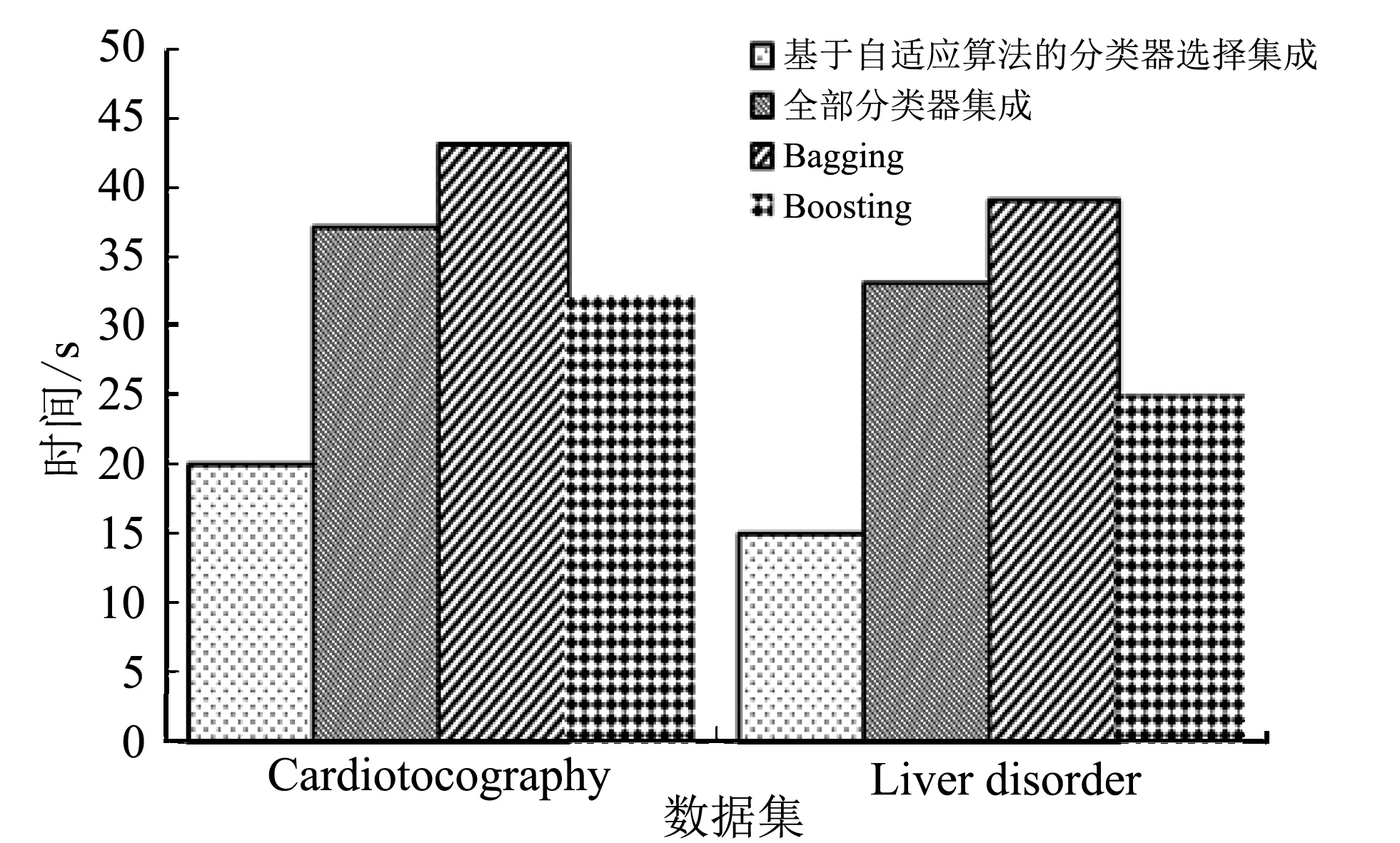
图 4 不同分类器判决时间Fig.4 Decision time of different classifiers

图 4 显示， 本文方法构建的分类器可显著缩短判别时间. 这与本文在个体分类器选择时使用的策略有关. 由于无需考虑各分类器在整体样本的分类精度， 所以减少了计算的工作量， 缩短了判别时间. RF算法在数据分类时花费时间最长， 原因在于该算法依赖的是决策树， 复杂度增加时， 决策树不可避免增加， 导致低效率.

3.5 集成分类器的稳定性实验

分别从Cardiotocography和Liver disorder两个数据集中， 选取不同规模的数据进行测试， 结果如图 5 和图 6 所示.

图 5 Cardiotocography数据集上的稳定性Fig.5 Stability on Cardiotocography

图 6 Liver disorder数据集上的稳定性Fig.6 Stability on Liver disorder

图 5 和图 6 表明， 本文方法构建的SVM集成分类器的准确度始终高于其它两种方法. 进一步扩大数据规模， 准确率始终高于其它三种分类器的判别效果， 说明了该分类器的性能具有一定的可靠性.

4 结 论

SVM集成的关键是如何择优选取个体分类器. 本文从分类性能、 判别时间及稳定性方面， 将建立的分类器与其它常用集成分类器进行实验对比.

结果显示， 本文提出的方法， 在UCI的两个医学数据集的分类中， 无论在分类的准确度还是灵敏度及特异度方面， 均高于其它的集成方法. 选取不同规模的数据进行稳定性实验， 本文方法构建的分类器始终具有一定的优势， 说明本文提出的方法在实践中具有一定的稳定性和可靠性.

比较几种方法的分类判别时间， 结果显示， 本文提出的方法所需的时间最短， 利用Bagging中的RF算法判决时， 时间最长， 反应了该算法在解决复杂问题时， 因决策树增多而导致的低效率.

另外， 本文提出的方法最大的优势还在于动态性和自适应性. SVM集成中的各个分类品成员， 以及各成员分类器在集成判别中的权重， 都不是一成不变的， 而是随着待定样本特征的变化动态调整.