聚驱定向井抽油杆柱力学模型及扶正器优化布置研究
(大庆油田工程有限公司,黑龙江 大庆163453)
随着国内大部分油田进入开发的中后期,聚合物驱抽油机井数量逐渐增加。聚驱井产出液的黏弹性使得抽油杆柱受到一个与井眼垂直的径向力,径向力与阻力、摩擦力共同作用,导致下冲程时中和点以下杆柱弯曲,造成杆管偏磨,特别是在具有一定斜度的定向井中,杆断、管漏等现象时有发生[1]。
朱君、常瑛、黄善波等人分别通过理论和试验方法,给出了聚驱井中抽油杆柱法向力的计算方法,并通过有限元法预测了杆管偏磨点的位置[2-4];孙智等人通过室内试验,分析了聚驱井杆管偏磨机理,并提出了相应的防偏磨措施[5];栾中伟、冯春、王超等人分别提出了一些防偏磨的配套措施[6-7]。研究认为,聚驱井中黏弹性的采出液会增加杆柱的法向力,加剧杆管之间的偏磨,但计算模型各异,计算结果也不相同,且对定向井中扶正器的布置方案研究较少。本文采用三次样条插值方法,预测任意井深处的井斜角与方位角参数,并建立杆柱的力学模型,分析抽油杆柱的受力情况,推导出抽油杆柱失稳间距方程,并通过MATLAB软件编程求解。
1 定向井井眼轨迹预测
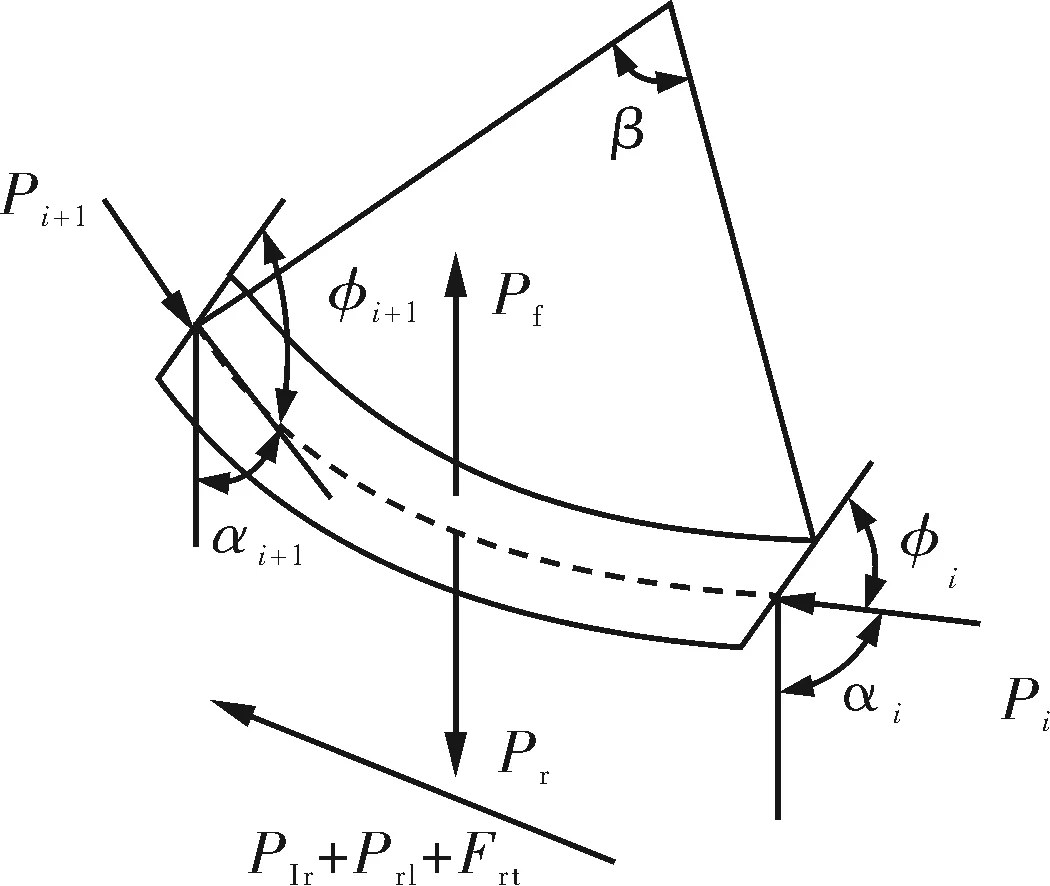
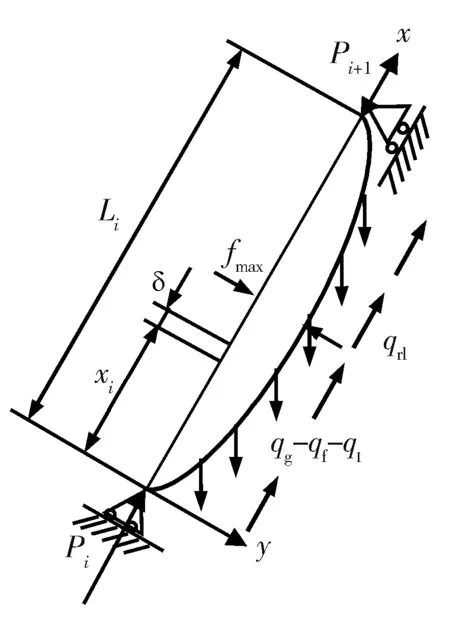
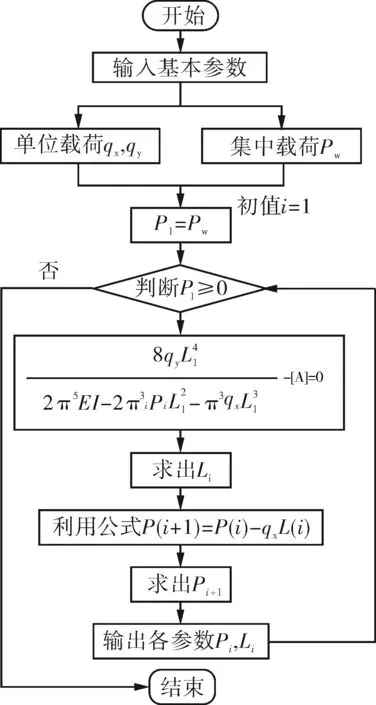
设定在井轴方向[a,b] 长度上,定义一组测试点,井轴方向深度:a=x1 则有井斜角函数α1,α2,…,αN; 方位角函数β1,β2, …,βN。 井斜角函数和方位角函数均为沿井轴方向变化的函数。由三次样条函数的定义可知,能够将三次井眼样条函数S(x)和Q(x)(S(x)和Q(x)在[a,b]上)分别插值于井斜角α和方位角β的三次井斜样条函数和三次方位样条函数上,这2个函数统称为三次井眼样条函数[8-10]。 由三次样条函数性质,可将三次井眼样条函数S(x)和Q(x)表示为 (1) (2) 其中:Mk=S"(xk),Mk-1=S"(xk-1),mk=Q"(xk),mk-1=Q"(xk-1)。 为了确定S(x)和Q(x),必须求出Mk,mk(K=0,1,2,……,N)。 经推导,可以得到确定Mk,mk的线性方程组为 (3) (4) 式(3)~(4)可以写成如下矩阵形式: (5) (6) 式(5)~(6)是三对角方程组,用"追赶法"求解,求出M1,M2…MN,和m1,m2…mN,代入式(1)~(2),可求出[a,b] 井段上任意井深处的井斜角S(x)和方位角Q(x) ,从而确定井眼轨迹上任一点的空间位置。 由于斜井要考虑井斜、方位、狗腿角等因素,比较复杂,故将抽油杆划分为微元段进行分析。 假设井下抽油杆柱为柔性杆,不考虑抽油杆截面上的剪切力和弯矩,取任意井深处长为dl的抽油杆柱作为研究对象,其受力如图1所示。 图 1 任意微段抽油杆受力示意 1) 抽油杆柱所受的重力。 Pr=qgdl·cosα=ρrArgdl·cosα (7) 式中:Pr为抽油杆柱沿轴向分布的重力,N;qg为单位抽油杆在空气中的重力,作用方向为垂直向下,N/m;ρr为抽油杆密度,ρr=7 850 kg/m3;Ar为抽油杆的横截面积,mm2,g为重力加速度,g=9.8 m/s2;α为该微元井段的井斜角,(°)。 2) 抽油杆柱所受的浮力。 Pf=qfdl·cosα=ρlArgdl·cosα (8) 式中:qf为单位抽油杆在井液中所受的浮力,作用方向为垂直向上,N/m;ρl为井液密度,ρl=fwρw+(1-fw)ρ0,ρw、ρ0分别为水、原油的密度,kg/m3。 3) 抽油杆柱的惯性力。 (9) 4) 抽油杆柱与井液间的摩擦力。 (10) 5) 杆管间摩擦力。 Frt=fNrt (11) 式中:Frt为杆管间的摩擦力,方向沿井轴方向向上,N;f为杆与管内壁间的摩擦因数,其值为0.05~0.1[11];Nrt为杆管之间的法向接触力,N。 将杆管之间的法向接触力分解在互相垂直的2个平面上,其一为狗腿平面上,由轴向力和杆柱重力引起的侧向力N1,其二为由杆柱重力引起的侧向力N2。 (12) (13) 油管与抽油杆间的挤压力为 (14) 式中:Pi、Pi+1分别为所选取的微元体上下两端轴向力;αi、αi+1、φi、φi+1分别为微元体的井斜角和方位角;β为狗腿的角度,cosβ=cosα1cosα2+sinα1sinα2cos(φ2-φ1)。 6) 抽油泵柱塞与衬套间的摩擦力。 (15) 式中:Ff为抽油泵柱塞与衬套间的摩擦力,作用方向沿抽油杆柱轴线向上,N;Dp为柱塞直径,mm;δ为柱塞与泵筒的间隙,由抽油泵标准可知,柱塞与泵筒间的配合间隙共有3个等级,为方便计算取其平均值0.053 mm[12]。 7) 井液流过游动阀时的水力阻力。 (16) 8) 泵充不满引起的液击载荷。 (17) 式中:cr、cl分别为声波在抽油杆和井液中的传播速度,取cr=5 200 m/s ,cl=400 m/s ;vs为柱塞与液面接触瞬间的速度,泵的充满度为50%时冲击力最大,取vs=vmax。 抽油杆柱在运动过程中主要承受2种载荷的影响:一种是作用在杆柱底部泵端的轴向集中载荷Pw,Pw=Ff+Fv+Py+Fcj;另一种为均匀分布在杆柱上的单位载荷,可分解为沿杆体作用的轴向均布载荷qx,以及垂直于杆柱轴线的径向均布载荷qy,qx=(qg-qf-qI)cosα-qrl,qy=(qg-qf-qI)sinα+f。 建立杆柱简支梁模型,取模型的任意一跨进行分析,如图2所示。 图2 考虑法向力及井斜影响的简支梁模型 模型中抽油杆的近似挠曲线方程为 (18) 式中:A1,A2,…,An为待定系数。鉴于三角级数求解精度极高,取n=1时的计算精度就能满足工程设计要求。 令:A1=A为挠曲线方程的近似解。 (19) 需满足的边界条件为 yi|x=0=0;yi|x=li=0;yi"|x=0=0;yi"|x=li=0 (20) 式(20)的一、二阶倒数分别为 (21) (22) 由弹性稳定理论可知,轴向压力在位移δ上所做的功为 (23) 式中:A为抽油杆弯曲的最大挠度,m;Li为相邻两个扶正环间的距离,m;Pi为下端扶正环所受的轴向力,N。 轴向均布载荷沿杆柱轴向所做的功为 (24) 式中:qx为作用在杆柱轴向均布载荷,N/m。 横向均布载荷沿垂直杆柱轴向所做的功为 (25) 式中:qy为作用在垂直杆柱轴向方向上的均布载荷,N/m。 抽油杆弯曲变形增加的弹性应变能为 (26) 系统的势能为 (27) (28) 相邻两扶正环间抽油杆的最大挠度为 (29) 为保证在抽油杆发生弯曲变形后不与油管产生接触,则扶正环间距应满足式(30)。 (30) 相邻两扶正环间抽油杆的失稳方程为 (31) 该模型研究的是中和点以下至泵端位置,若对中和点以上杆柱进行分析时,由于抽油杆处于受拉状态,则改变其受力方向,相应的失稳方程为 (32) 斜井需要考虑由于井斜和方位因素引起的抽油杆与油管间的摩擦力,其受力计算满足P(i+1)=P(i)-qx×L(i)+Frt,代入抽油杆失稳方程逐次迭代,可得其余各简支梁的轴向压力Pi和长度值Li;由此确定第i个扶正器安放的位置,直至中和点。 利用前面的分析理论以及建立的数学模型编制程序进行求解,程序流程如图3所示。程序界面如图4。 图3 求解程序流程 大庆油田某采油厂6口定向井自井口开始计算,第1~3根抽油杆上每根杆布置1个扶正环,第4~11根每根抽油杆上布置3个扶正环,第12~23根抽油杆每根杆上布置4个扶正环,从第24根杆开始直至接泵杆以上位置每根杆布置3个扶正环。但据油田统计结果发现,该方案下抽油杆偏磨问题依然很严重,检泵周期最长不超过310 d。6口斜井基本参数如表1。 2016-08,针对现场提供的6口斜井数据进行扶正环优化计算,如表2所示。并按照表2进行了扶正器的重新布置,该6口井无故障工作时间已达630 d以上。 由表2可见,6口斜井优化后的扶正环数量平均减少率达到17.47%,扶正环的布置方案变化范围主要集中在4环杆位置处,各因素对扶正环布置的影响规律与直井相似。第1个4环杆为泵上接近泵端位置,第2个4环杆为造斜段位置,数量与造斜段跨度有关。 图4 程序界面 表1 6口斜井基本参数 表2 6口斜井扶正环优化配置方案 1) 通过建立抽油杆柱的简支梁模型,分析了抽油杆柱的受力情况,推导出了考虑井斜因素下的抽油杆柱失稳间距方程,并利用MATLAB软件编制了相应的求解程序。 2) 对大庆油田某厂6口定向井进行了扶正器的优化布置,通过优化计算,扶正器的安装个数平均减少了17.47%,无故障工作时间大幅延迟。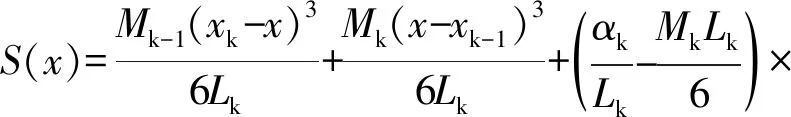

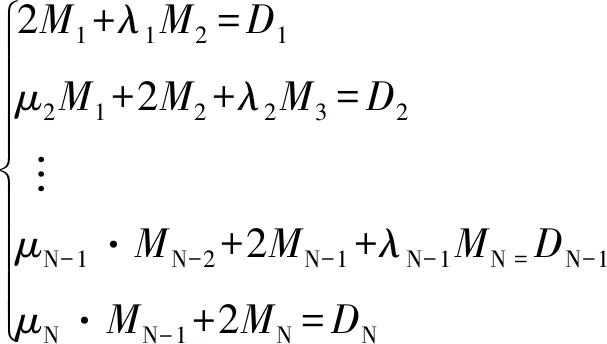
2 定向井杆柱受力分析
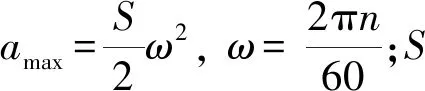
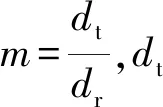

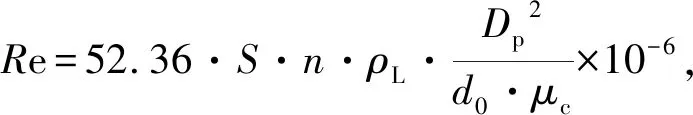
3 杆柱失稳模型

4 求解方法
5 斜井实例计算
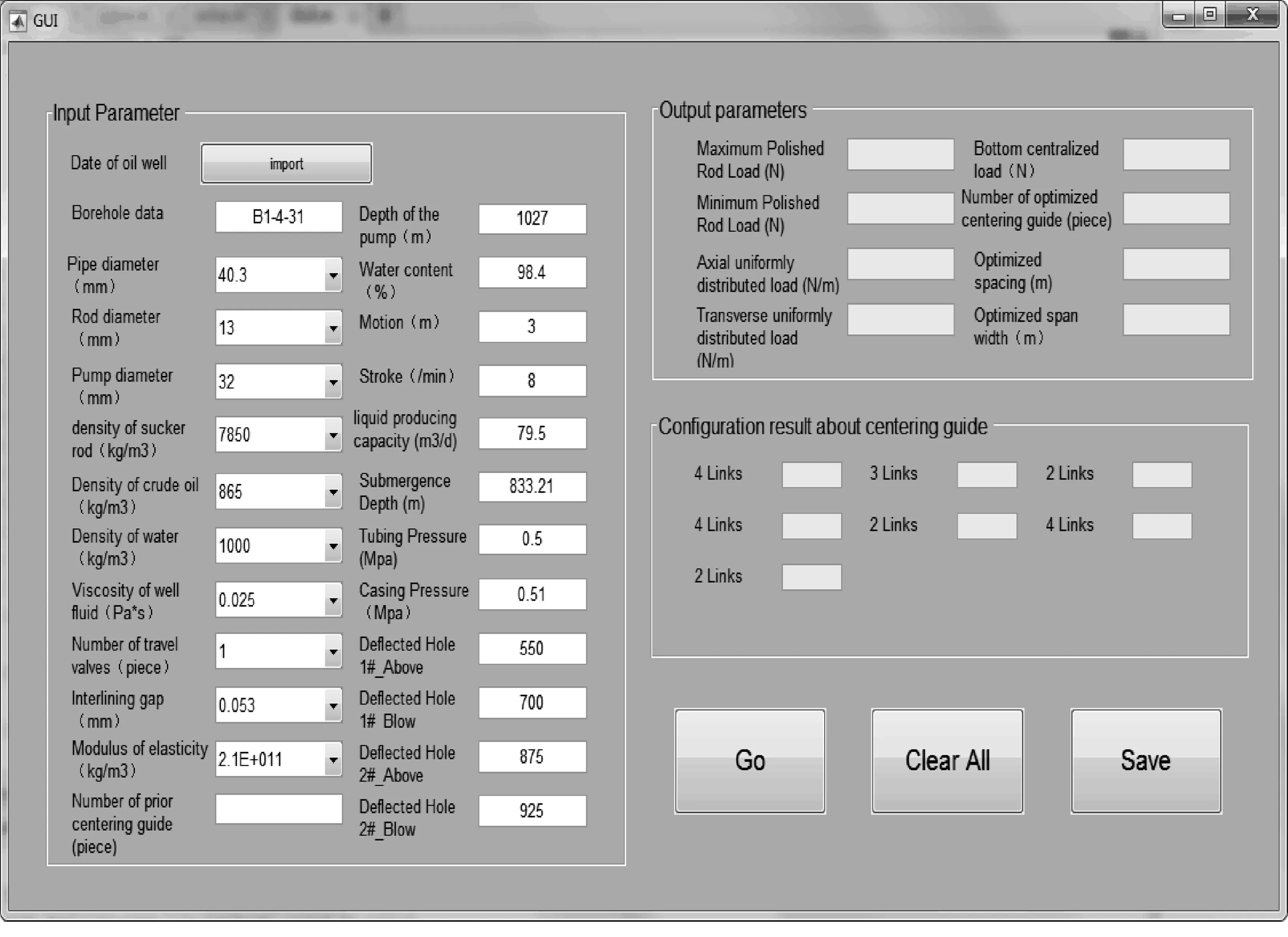
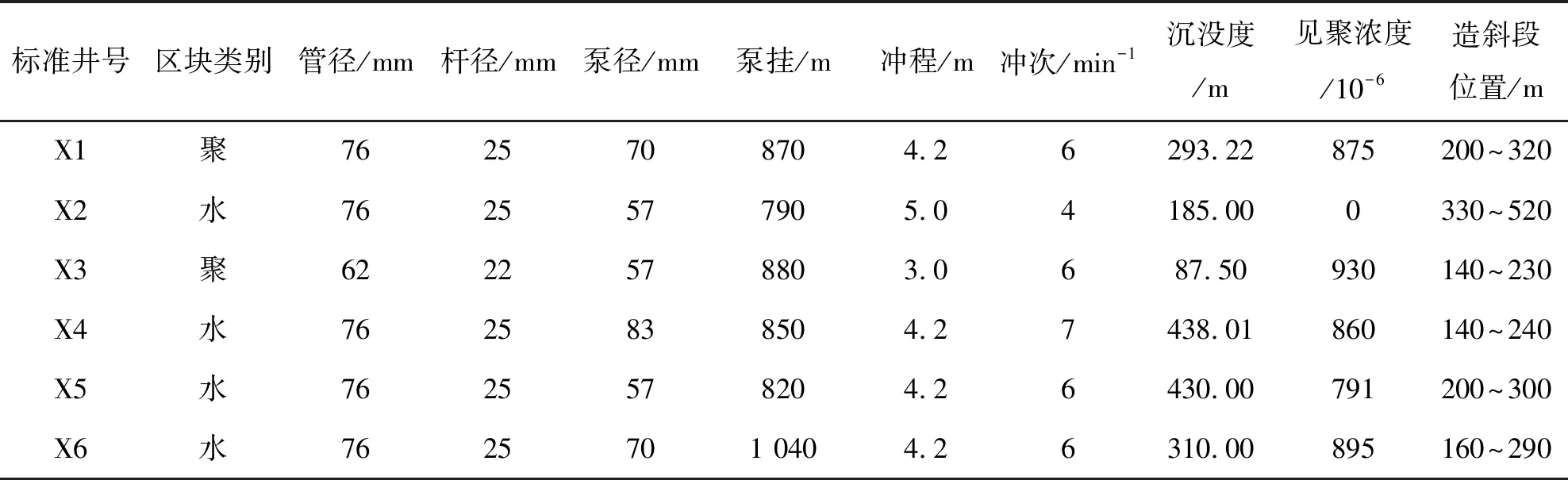
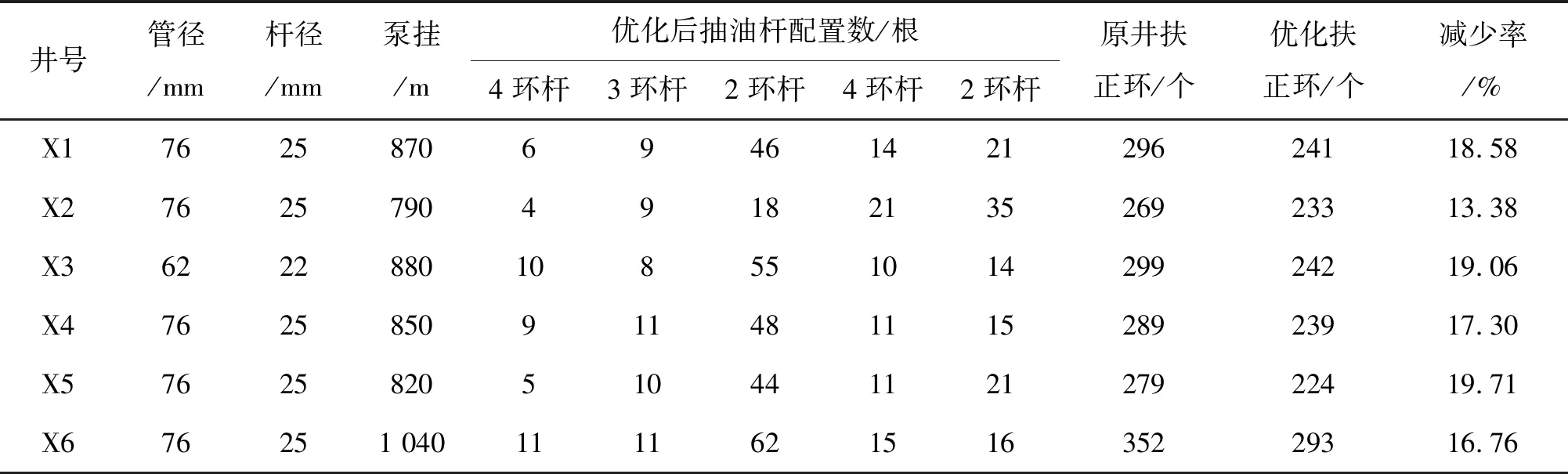
6 结论

